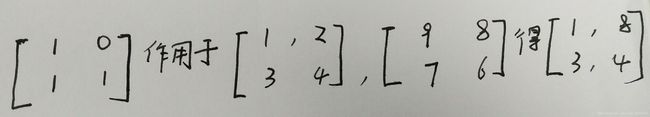scipy库中的stats模块
scipy简介
scipy是Python的一个科学计算库,它导入了numpy库中的所有命名空间,而且包含其他的一些库。其中的stats库是一个提供统计功能的库,import scipy.stats 进行导入
先学习一部分关于scipy模块的基础知识
scipy基础功能
与numpy交互
scipy模块建立在numpy模块的基础上,在scipy模块的顶层包含numpy模块的所用方法,但是调用这些方法还是在numpy模块中调用比较好,调用scipy的某些模块中的方法,需要这样
>>> from scipy import some_module
>>> some_module.some_function()索引技巧
一些类示例使用了特殊的切片方法,来快速构建数组
使用原有的组合数组的方法concatenate可以将数组按照指定的维度组合起来
>>> a = np.array([[1, 2], [3, 4]])
>>> b = np.array([[5, 6]])
>>> np.concatenate((a, b), axis=0) # 表示列方向
array([[1, 2],
[3, 4],
[5, 6]])
>>> np.concatenate((a, b.T), axis=1) # 表示行方向
array([[1, 2, 5],
[3, 4, 6]])
>>> np.concatenate((a, b), axis=None)
array([1, 2, 3, 4, 5, 6])
# 这些叠加操作可以通过画出矩阵图进行理解scipy提供了可以简化操作的方法,在第一行代码中,有三个数组参数,[3], [0, 0, 0, 0, 0]以及[-1. -0.77777778 -0.55555556 -0.33333333 -0.11111111 0.11111111. 0.33333333 0.55555556 0.77777778 1.],然后将这三个数组以默认行的方向拼接,使用第二行中的代码,第三个数组本来要用arange方法生成,但是使用了一种独特的切片方法,-1和1指定了范围,10j指定了元素的数量,并没有直接指定步长,用10j来指定数量看起来有些奇怪,但是事实就是这样的用法,用这种方法时,端点是包括在内的,第一行代码为了将端点包括进去,不得不将第二个端点设置为1.002;另外这句代码中r表示行连接的意思,为了实现列连接,会使用字母c,对于二位数组c使用列连接,但是对于一维数组,c和r是一样的效果
>>> a = np.concatenate(([3], [0]*5, np.arange(-1, 1.002, 2/9.0)))
# 这是改进的版本
>>> a = np.r_[[3],[0]*5,-1:1:10j] # 3外面的中括号可写可不写还有一种数组拼接的方法。使用vstack函数:
np.vstack(p1, p2) #沿着列方向将两个数组拼接,当两个数组是一维数组时,两个数组的长度必须是一致的,会生成一个2×n的矩阵另外一个使用扩展切片表示法的方法是mgrid,最简单情况下,可以构造一维数组,和arange作用是一样的,这个方法允许使用10j这种复数的形式来指定两个端点之间的点数,对这个函数的用法还是有些不理解
>>> np.mgrid[0:5,0:5]
array([[[0, 0, 0, 0, 0],
[1, 1, 1, 1, 1],
[2, 2, 2, 2, 2],
[3, 3, 3, 3, 3],
[4, 4, 4, 4, 4]],
[[0, 1, 2, 3, 4],
[0, 1, 2, 3, 4],
[0, 1, 2, 3, 4],
[0, 1, 2, 3, 4],
[0, 1, 2, 3, 4]]])
>>> np.mgrid[0:5:4j,0:5:4j]
array([[[ 0. , 0. , 0. , 0. ],
[ 1.6667, 1.6667, 1.6667, 1.6667],
[ 3.3333, 3.3333, 3.3333, 3.3333],
[ 5. , 5. , 5. , 5. ]],
[[ 0. , 1.6667, 3.3333, 5. ],
[ 0. , 1.6667, 3.3333, 5. ],
[ 0. , 1.6667, 3.3333, 5. ],
[ 0. , 1.6667, 3.3333, 5. ]]])形状操纵
在官方文档中提到:有一些函数用来压缩n维数组,还有分割数组,但是并没有指出,可能在API手册中
多项式
在scipy包中有两种处理一元n次多项式的方法。第一种方法是使用numpy包中的ploy1d类,这个类接收多项式系数或者多项式的解作为参数。这个方法可以以代数表达式的形式执行积分、微分、求值操作。下面这些代码是官方文档中给出的
>>> from numpy import poly1d
>>> p = poly1d([3,4,5])
>>> print(p)
2 # 这个看起来很奇怪的2是指幂次,就是x^2,这个意思
3 x + 4 x + 5
>>> print(p*p) #表示两个多项式相乘
4 3 2
9 x + 24 x + 46 x + 40 x + 25
>>> print(p.integ(k=6))
3 2
1 x + 2 x + 5 x + 6
>>> print(p.deriv())
6 x + 4
>>> p([4, 5])
array([ 69, 100])以下是对多项式简单操作的一些总结:
- p = poly1d([1, 2, 3]) 用来生成一个多项式: 1*x^2 + 2*x + 3
- p(0.5) 求x = 0.5时多项式的值
- p.r 令多项式右边等于0,然后求多项式的根,并以数组的形式返回,得到[-1.+1.41421356j -1.-1.41421356j]
- p(p.r) 返回机器(0, 0)的精度
- p.c 用数组形式返回多项式的系数
- p.r 返回多项式的阶数
- p[k] 返回k次项的系数
- p**k 返回多项式的k次幂形成的多项式
- numpy.square(p) 对p多项式的每一项的系数平方。然后以数组的形式返回
- p = np.poly1d([1,2,3], variable='z') 将多项式中的未知数指定为z然后生成多项式
- np.poly1d([1, 2], True) 这句代码指定多项式的根为[1, 2]然后生成多项式
- np.poly1d([1, -1]) * np.poly1d([1, -2]) 用两个一阶多项式构造了一个二阶多项式,可以联想到因式分解
- p.integ(k = 6) 对p多项式积分,积分常数为k
- p.deriv() 对多项式微分
还有一种处理多项式的方法是将多项式抽取为一个系数数组,数组第一个元素是最高次项的系数,然后用显示函数实现多项式的计算
向量操作
numpy提供的一个特性是类vectorize,将一个普通的python函数转换为一个“向量化函数”,看例子就明白了
>>> def addsubtract(a,b):
... if a > b:
... return a - b
... else:
... return a + b
这个函数的参数和返回值都是标量
>>> vec_addsubtract = np.vectorize(addsubtract)
返回一个函数(头一次知道函数可以当返回值,python真的一切皆为对象)
>>> vec_addsubtract([0,3,6,9],[1,3,5,7])
array([1, 6, 1, 2])这是向量版本的addsubtract函数。一般高性能的函数都是使用了向量特性
类型处理
这里面说的暂时用不到,先不仔细看了,和复数虚数有关
其他有用的功能
相位处理,有angle,unwrap函数;linspace, logspace以线性,对数尺度返回等元素等间隔分布的数组;然后先提一下where函数,它的用法如下,第一个参数是一个条件,如果条件为真,输出数组相应索引位置的值采用第一种值,如果条件为假,采用第二种值
>>> a = np.arange(10)
>>> a
array([0, 1, 2, 3, 4, 5, 6, 7, 8, 9])
>>> np.where(a < 5, a, 10*a)
array([ 0, 1, 2, 3, 4, 50, 60, 70, 80, 90])对于多维数组也是成立的
>>> np.where([[True, False], [True, True]],
... [[1, 2], [3, 4]],
... [[9, 8], [7, 6]])
array([[1, 8],
[3, 4]])其实条件就是一个掩膜
在numpy中有一个加强版的where函数 select,它的第一个参数是一个数组,这个数组里面是条件,第二个参数是一个长度为2的一维数组,分别指定条件为真为假时的值
>>> x = np.arange(10)
>>> condlist = [x<3, x>5]
>>> choicelist = [x, x**2]
>>> np.select(condlist, choicelist)
array([ 0, 1, 2, 0, 0, 0, 36, 49, 64, 81])还有其他一些有用的功能,比如factorial方法用来计算阶乘,还用很复杂的函数,在scipy.misc中可以找到
stats简介
介绍
这个包中的内容包括离散统计分布以及连续统计分布
随机变量
这个包中有很多实用的随机变量,可以通过使用info(stats)获得这些函数的状态和完整列表,但是我没成功,
常用方法
- stats.linregress(x, target_data) 这个方法是最小二乘法回归计算,第一次参数指定点的横坐标,第二个参数指定点的纵坐标,函数有五个返回值,分别是:斜率、截距、相关系数、t分布相关的一个参数、估计梯度标准误差,一般常用的是前三个参数
暂时先停一下!