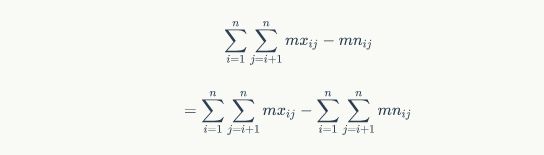【单调栈】区区区间间间

链接：https://ac.nowcoder.com/acm/problem/20806
来源：牛客网
 

题目描述

给出长度为n的序列a，其中第i个元素为ai，定义区间(l,r)的价值为v   l,r=max(ai−aj|l⩽i,j⩽r)

请你计算出∑n  l=1  ∑n   r=l+1vl,r∑l=1n∑r=l+1nvl,r

输入描述:

第一行输入数据组数T
对于每组数据，第一行为一个整数n，表示序列长度
接下来一行有n个数，表示序列内的元素

输出描述:

对于每组数据，输出一个整数表示答案

示例1

输入

复制

3
3
4 2 3
5
1 8 4 3 9
20
2 8 15 1 10 5 19 19 3 5 6 6 2 8 2 12 16 3 8 17 

输出

复制

5
57
2712

说明

对于一组测试数据的解释：
区间[1, 2]的贡献为：4 - 2 = 2
区间[1, 3]的贡献为：4 - 2 = 2
区间[2, 3]的贡献为：3 - 2 = 1
2 + 1 + 2 = 5.

备注:

T⩽20,n⩽105,0⩽ai⩽105T⩽20,n⩽105,0⩽ai⩽105

不保证数据随机生成！

 

学习博客：https://blog.csdn.net/Code92007/article/details/83689045

 

分析：

首先，问题可以转化为求

其中mx_ij是从i-j区间内的最大值,mn_ij是从i-j区间内的最小值

可以通过单调栈维护每个点作为最大值的区间，统计以该点为最大值的区间数量

以a[i]为区间最大值，向左维护到l[i]，向右维护到r[i]，即从l[i]-r[i]区间内a[i]都是最大值

数量的求法：

分两种情况：

①：a[i]作为端点，即从l[i]到r[i]内再选一点作为另一个端点，共有r[i]-l[i]种情况

②：a[i]作为区间中的一个点，即从l[i]到i内选一个左端点，i到r[i]内选一个右端点，共有(i-l[i])*(r[i]-i)种情况

两种情况求和乘上a[i]即可求出以a[i]为最大值的区间的和

最小值的和可以把a[i]=-a[i]即可求出最小值的和，与前面的负号正好抵消

 

 

代码：

//所有变量都开long long

#include
using namespace std;
const int INF=INT_MAX;
const long long LLINF=LONG_MAX;
const int mod=1e6+3;
typedef long long ll;
ll l[100307],r[103007];
ll a[100307];
ll ac(ll n)
{
    memset(l,0,sizeof(l));
    memset(r,0,sizeof(r));
    stack s,t;
    for(ll i=1;i<=n;i++)
    {
        while(s.size()&&a[i]>=a[s.top()])
        {
            s.pop();
        }
        if(!s.size())   l[i]=1;
        else    l[i]=s.top()+1;
        s.push(i);
    }
    for(ll i=n;i;i--)
    {
        while(t.size()&&a[i]>a[t.top()])
        {
            t.pop();
        }
        if(!t.size())   r[i]=n;
        else    r[i]=t.top()-1;
        t.push(i);
    }
    ll ans=0;
    for(ll i=1; i<=n; i++)
    {
        ans+=1LL*a[i]*1LL*((r[i]-l[i])+(i-l[i])*(r[i]-i));
    }
    return ans;
}
int main()
{
    ll t;
    cin>>t;
    while(t--)
    {
        ll n;
            cin>>n;
        for(ll i=1; i<=n; i++)
            cin>>a[i];
        ll ans=ac(n);
        for(ll i=1; i<=n; i++)
            a[i]=-a[i];
        ans+=ac(n);
        cout<