深度优先遍历DFS专题: Leetcode 207 课程表 + Leetcode 802 找到最终的安全状态
深度优先遍历DFS专题: Leetcode 207 课程表 + Leetcode 802 找到最终的安全状态
Leetcode 207 课程表
题目描述
难度中等226收藏分享切换为英文关注反馈现在你总共有 n 门课需要选,记为 0 到 n-1。
在选修某些课程之前需要一些先修课程。 例如,想要学习课程 0 ,你需要先完成课程 1 ,我们用一个匹配来表示他们: [0,1]
给定课程总量以及它们的先决条件,判断是否可能完成所有课程的学习?
示例 1:
输入: 2, [[1,0]]
输出: true
解释: 总共有 2 门课程。学习课程 1 之前,你需要完成课程 0。所以这是可能的。
示例 2:
输入: 2, [[1,0],[0,1]]
输出: false
解释: 总共有 2 门课程。学习课程 1 之前,你需要先完成课程 0;并且学习课程 0 之前,你还应先完成课程 1。这是不可能的。
题解:
这题的问题是:是否能够修完所有的课。
而修完所有课的先决条件是,这门课的后继节点不可能是这门课的前驱节点,也就是说,不存在环。因此这题就很简单,用一个深度优先搜索判断有向图中是否有环,就能判定是否能够修完。
因此思路非常简单,先构建一个图,然后再用图的深度优先搜索就能得到结果:如果一个白节点的后续是灰节点,就说明遇到了环。
代码如下:
def canFinish(numCourses, prerequisites):
def engraph(numCourses, lst):
Adj = dict()
for i in range(0, numCourses):
Adj[i] = set()
for i in lst:
Adj[i[1]].add(i[0])
return Adj
def Whether_Loop_DFS(start, white, Adj):
gray = [start]
black = set()
while white:
white = white - set(gray) - black
vertex = gray[-1]
temp = Adj[vertex] - black
for i in temp:
if i in gray:
return False
if temp:
for i in temp:
gray.append(i)
break
else:
black.add(vertex)
gray.remove(vertex)
if not gray:
temp = white - black
if temp:
gray = [list(temp)[0]]
return True
if not prerequisites:
return True
Adj = engraph(numCourses, prerequisites)
node_set = set(Adj.keys())
Result = Whether_Loop_DFS(prerequisites[0][1], node_set, Adj)
return Result
执行时间:628 ms
使用内存:14 MB
虽然有点慢,但还是能通过测试的
Leetcode 802 找到最终的安全状态
题目描述
在有向图中, 我们从某个节点和每个转向处开始, 沿着图的有向边走。 如果我们到达的节点是终点 (即它没有连出的有向边), 我们停止。
现在, 如果我们最后能走到终点,那么我们的起始节点是最终安全的。 更具体地说, 存在一个自然数 K, 无论选择从哪里开始行走, 我们走了不到 K 步后必能停止在一个终点。
哪些节点最终是安全的? 结果返回一个有序的数组。
该有向图有 N 个节点,标签为 0, 1, …, N-1, 其中 N 是 graph 的节点数. 图以以下的形式给出: graph[i] 是节点 j 的一个列表,满足 (i, j) 是图的一条有向边。
示例:
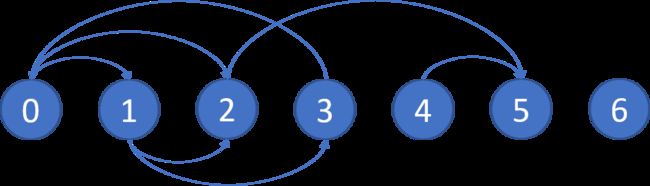
输入:graph = [[1,2],[2,3],[5],[0],[5],[],[]]
输出:[2,4,5,6]
这里是上图的示意图。
题解
这个问题的解题思路如下:如标题,使用深度优先遍历 如果碰到有环,则将前面遇到的所有节点都是不可能的。(这里要注意自环的情况)
碰到环有两种情况:
- 如果碰到一个节点,这个节点的后继属于不可能的,那这个节点也不可能。
- 如果碰到一个节点,这个节点的后继属于灰色,则这个节点不可能。(这就是普通的深度优先遍历碰到环的情况)
那这个问题就很简单了,如同上方课程表的实现一样,找环即可。
有个很坑的事情,就是提交的时候都一定要是升序的,还得对节点进行排序,浪费一个排序 O ( N log N ) O(N \log N) O(NlogN) 的时间。
代码如下:
class Solution(object):
def eventualSafeNodes(self, graph):
# 初始化
n = len(graph)
white = set(range(1, n))
gray = [0]
black = set()
invalid = set()
# DFS
cur = 0
while gray:
cur = gray[-1]
if not graph[cur]:
black.add(gray.pop())
if not white:
while gray:
temp = gray.pop()
if temp in graph[temp]:
invalid.add(temp)
continue
if not (set(graph[temp]) & invalid):
black.add(temp)
break
else:
if not gray:
gray.append(white.pop())
continue
nxt = graph[cur].pop()
if (nxt in gray) | (nxt in invalid) | (nxt == cur):
for i in gray:
invalid.add(i)
if white:
gray = [white.pop()]
continue
else:
break
gray.append(nxt)
if nxt in white:
white.remove(nxt)
else:
gray.pop()
if white:
black = black | white
black = list(black)
black.sort()
return black
执行结果
执行时间:848 ms
内存消耗:18.1 MB