三角形的四心
打比赛遇到一道外心的题(HDU - 6206),不去搜板子,根本不会,所以打算总结一下三角形的四心。
给出三角形的三个点 A(x1,y1),B(x2,y2),C(x3,y3);∠A,∠B,∠C A ( x 1 , y 1 ) , B ( x 2 , y 2 ) , C ( x 3 , y 3 ) ; ∠ A , ∠ B , ∠ C 的对边分别为 a,b,c a , b , c 。
重心:
定义:三条中线的交点。·常用 G G 表示。
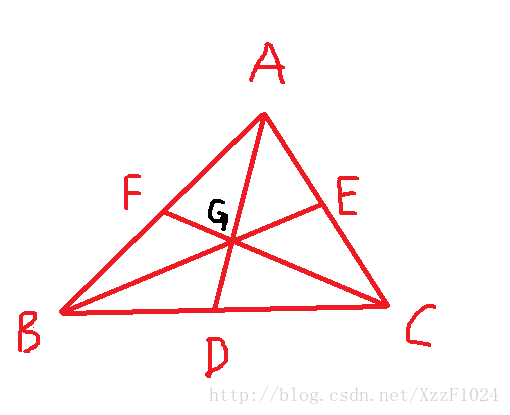
性质:
1. 重心坐标 G(x1+x2+x33,y1+y2+y33) G ( x 1 + x 2 + x 3 3 , y 1 + y 2 + y 3 3 )
point GravityCenter(point A, point B, point C) {
double Gx = (A.x + B.x + C.x) / 3;
double Gy = (A.y + B.y + C.y) / 3;
return point(Gx, Gy);
}
2. AG=2GD,BG=2GE,CG=2FG A G = 2 G D , B G = 2 G E , C G = 2 F G
3. S△AGC=S△AGB=S△BGC S △ A G C = S △ A G B = S △ B G C
4. GA→+GB→+GC→=0⃗ G A → + G B → + G C → = 0 →
性质4证明:
外心:
定义:三条中垂线的交点,常用 O O 来表示。
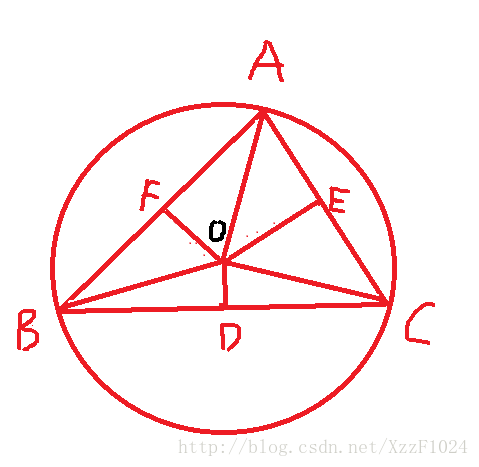
性质:
1. 外心坐标:有点复杂,,,
设外心坐标为 O(x0,y0) O ( x 0 , y 0 ) ,外接圆半径为 r r 。那么外接圆的方程就为 (x−x0)2+(y−y0)2=r2 ( x − x 0 ) 2 + ( y − y 0 ) 2 = r 2 。
由此可得:
(1)−(2),(2)−(3) ( 1 ) − ( 2 ) , ( 2 ) − ( 3 ) ,化简之后可得:
令:
a=(x1−x2)b=(y1−y2) a = ( x 1 − x 2 ) b = ( y 1 − y 2 )
c=(x1−x3)d=(y1−y3) c = ( x 1 − x 3 ) d = ( y 1 − y 3 )
e=(x21−x22)+(y21−y22)2f=(x21−x23)+(y21−y33)2 e = ( x 1 2 − x 2 2 ) + ( y 1 2 − y 2 2 ) 2 f = ( x 1 2 − x 3 2 ) + ( y 1 2 − y 3 3 ) 2
运用简单的线性代数知识(好像是叫克拉默法则),即可求得:
将相应字母代入,可得(公式太长 …… … … ):
还是代码来得实在:
point CircumCenter(point A, point B, point C) {
double d = 2 * ((A.x - B.x) * (A.y - C.y) - (A.x - C.x) * (A.y - B.y)); //分母
double a = (A.y - C.y) * ((A.x * A.x - B.x * B.x) + (A.y * A.y - B.y * B.y)); //Ox的分子
a = a - (A.y - B.y) * ((A.x * A.x - C.x * C.x) + (A.y * A.y - C.y * C.y));
double b = (A.x - B.x) * ((A.x * A.x - C.x * C.x) + (A.y * A.y - C.y * C.y)); //Oy的分子
b = b - (A.x - C.x) * ((A.x * A.x - B.x * B.x) + (A.y * A.y - B.y * B.y));
double Ox = a / d;
double Oy = b / d;
return point(Ox, Oy);
}
我还从一本书上看到另外一种求法,比较简洁,但不太懂:
point CircumCenter(point A, point B, point C) {
double a1 = B.x - A.x, b1 = B.y - A.y, c1 = (a1 * a1 + b1 * b1) / 2;
double a2 = C.x - A.x, b2 = C.y - A.y, c2 = (a2 * a2 + b2 * b2) / 2;
double d = a1 * b2 - a2 * b1;
double Ox = A.x + (b2 * c1 - b1 * c2) / d;
double Oy = A.y + (a1 * c2 - a2 * c1) / d;
return point(Ox, Oy);
}
2. ∠A=12∠BOC,∠B=12∠AOC,∠C=12∠AOB ∠ A = 1 2 ∠ B O C , ∠ B = 1 2 ∠ A O C , ∠ C = 1 2 ∠ A O B
在说垂心之前,先说一个欧拉的定理:三角形外心 O O 、重心 G G 、垂心 H H 三点共线,且 OG:GH=1:2 O G : G H = 1 : 2 (此直线叫做欧拉线)
证明:,,,,,, △OGM∼△HGA △ O G M ∼ △ H G A
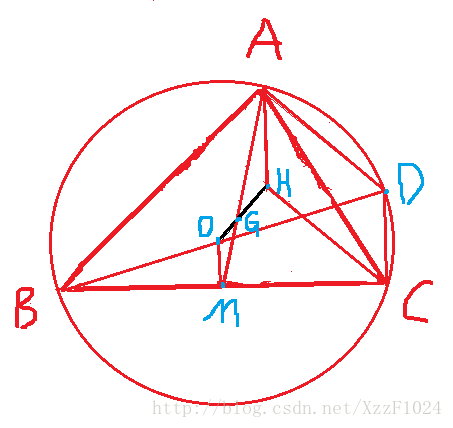
所以,若已知三角形外心 O O 、重心 G G 、垂心 H H 三点中任意两点的坐标,都可求得第三点的坐标。
垂心:
定义:三条垂线的交点,常用 H H 表示。
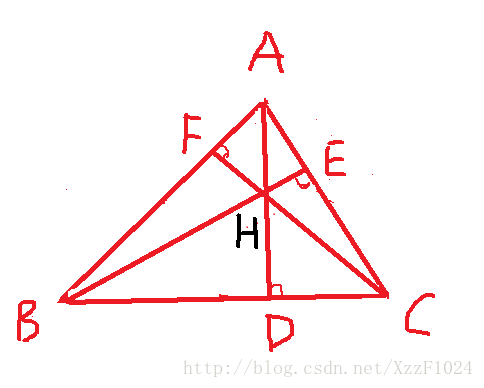
性质:
1. 垂心坐标: H(3Gx−2Ox,3Gy−2Oy) H ( 3 G x − 2 O x , 3 G y − 2 O y )
ps:其实也可以想外心那样推,,,,要是吃饱了没事干,
point VerticalCenter(point A, point B, point C) {
return 3.0 * GravityCenter(A, B, C) - 2.0 * CircumCenter(A, B, C);
}
内心:
定义:三条角平分线的交点,常用 I I 表示。
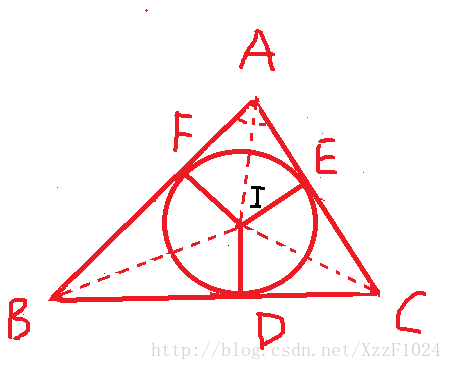
性质:
1.内心坐标: I(ax1+bx2+cx3a+b+c,ay1+by2+cy3a+b+c) I ( a x 1 + b x 2 + c x 3 a + b + c , a y 1 + b y 2 + c y 3 a + b + c )
point InternalCenter(point A, point B, point C) {
double a = dis(B, C);
double b = dis(A, C);
double c = dis(A, B);
double Ix = (a * A.x + b * B.x + c * C.x) / (a + b + c);
double Iy = (a * A.y + b * B.y + c * C.y) / (a + b + c);
return point(Ix, Iy);
}
2. 点 I I 是 △ABC △ A B C 的内心 ⇔ ⇔ aIA→+bIB→+cIC→=0⃗ a I A → + b I B → + c I C → = 0 →
证明:先略,,,
2. P P 为平面任意一点,有 PI→=aPA→+bPB→+cPC→a+b+c P I → = a P A → + b P B → + c P C → a + b + c
证明:先略,,,
再说一个欧拉的定理:
△ABC △ A B C 外心为 O O ,内心为 I I , R和r R 和 r 分别为外接圆和内接圆的半径,则有:
|OI→|2=R2−2Rr | O I → | 2 = R 2 − 2 R r

△IMC∼△DBH △ I M C ∼ △ D B H