树状数组简单梳理(上)
树状数组简单梳理(上)
背景
平时做题时我们经常会碰到一类问题:
有一个数组,多次往这个数组上某个点的值增加k,再多次求数组上某个区间所有数组之和。
有一个数组,多次往这个数组某个区间上的值增加k,再多次求某个点的值。
以第一个问题为例,用正常的思路想就有如下操作
//多次往某个点增加k
while(t1--)
a[x]+=k;
//多次求某个区间所有数字之和
while(t2--)
{
for(int i=l;i<=r;i++)
sum+=a[i];
}虽然直观易懂,但如果多次要求往某个数增加k,并多次求不同的区间和,它的时间复杂度为O(KN),若区间过长且求和次数过多,就无法承受。
那么该怎么办呢,这里就要请出树状数组了,树状数组基本应用就是用来解决这些带有关键词多次、单点、区间、修改、查询(求和) 的问题。
树状数组原理
lowbit运算
先介绍一下树状数组中用到的二进制的按位运算,一个是&运算,称为按位与运算,当对两个数进行&运算,就有有0出0,全1出1这个结果,例如1&1=1,0&1=0,1&0=0,0&0=0 ,若是十进制的数,则先将它转化为二进制,再对对应位进行上述运算;还有一个是~运算,称为按位非运算,具体表现就是0变为1,1变为0,十进制数转换为二进制再进行上述变换。
lowbit运算,用到了这两个操作:lowbit(x)=x&(-x) 。说是用到了这两个操作,为什么只看到了&,没有看到了~呢,因为 ~藏在了-x里。在计算机中把一个整数x取相反数·x,就是把x的二进制最右边的1左边的每一位取反(~运算)。通过它可以很容易推得lowbit(x)=x&(-x)就是取x得二进制最右边得1和它右边所有的0(可以自己操作验证一下),因此它一定是2的幂次,即1、2、4、8等,lowbit(x)也可以理解为能整除x的最大2的幂次。
树状数组的定义
树状数组其实还是一个数组(虽然看起来像多个数组),它是一个用来记录和的数组,类似于sum[i],只不过它存放的并不是前i个整数之和,而是i之前(包含i)lowbit(i)个整数之和。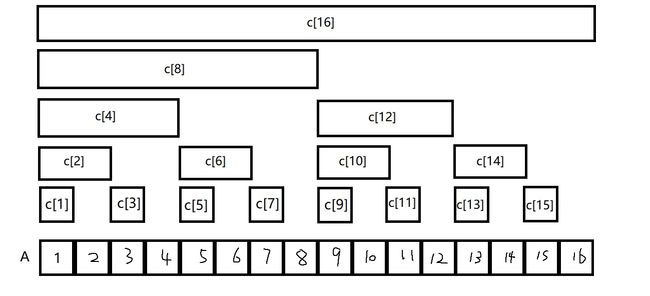
上图最底下的A代表原数组请忽略手写字体XD,,上面的C数组就是树状数组了。
A[1]到A[16]共16个元素,数组C[I]存放数组A中i号位之前lowbit(i)个元素之和 ,显然C[I]的覆盖长度是lowbit[i](也可以理解成管辖范围、势力范围、前lowbit(i)个A数组元素的父亲 )。
C[1]=A[1]
C[2]=A[1]+A[2]
C[3]=A[3]
C[4]=A[1]+A[2]+A[3]+A[4]
C[5]=A[5]
C[6]=A[5]+A[6]
C[7]=A[7]
C[8]=A[1]+A[2]+A[3]+A[4]+A[5]+A[6]+A[7]+A[8]
此处强调:树状数组的下标是从1开始的 ,C[I]覆盖lowbit[i]个原数组
树状数组函数设计
从一开始我们就知道,树状数组的构造需求来源于 更新 和 查找 这两步操作。因此我们需要设计两个函数
sum(x)
返回前x个数之和A[1]+A[2]+...A[x]
记sum(x)=A[1]+A[2]+...A[x],由于C[x]的覆盖长度是lowbit(x),即C[x]=A[ x-lowbit(x)+1 ]+A[ x-lowbit(x)+2 ]+...A[x]
结合两者可以得到:sum(x)=sum( lowbit(x) )+C[x], 所以sum(x)由如下代码实现
int sum(int x)
{
int sum=0;
for(;x>0;x-=x&-x)//x&-x就是lowbit(x)
sum+=c[x];//累加c[i],再把问题缩小为sum( x-lowbit(x) )
return sum;
}对二进制稍作模拟,可以得出sum(x)函数 的时间复杂度为O(logN) ,相比较与传统方法O(N),时间复杂度大大减小。
add(x,k)
将第x个数加上k,即A[X]=A[x]+k
虽然传统做法中,该操作时间复杂度只是O(1),即不用循环操作,但为了实现上面的sum函数,更新操作就要做出牺牲(即使牺牲了,两者加起来的时间复杂度仍然小于传统的O(N),这样整个程序的实现时间就被大大缩短了)。
要让sum函数能够顺利求和,这步对原数组A[x]增加k的操作就应该变为对树状数组C中能覆盖A[x]的那些元素增加k,理解这个变化对理解树状数组相当重要!!!
那么,如何找到覆盖A[x]的树状数组的元素呢?自然还是要用到lowbit运算。读者可以根据sum函数的解释,理解以下代码
void add(int x,int k)
{
for(;x<=n;x+=x&-x)
c[x]+=k;//让c[x]加上k,然后让c[ x+lowbit(x) ]加上k
}树状数组应用
有了对树状数组的理解,我们再回过头解决第一个问题
有一个数组,多次往这个数组上某个点的值增加k,再多次求数组上某个区间所有数组之和。
1.首先读入原数组的初始数据
memset(c,0,sizeof(c));//初始树状数组值为0
for(int i=1;i<=n;i++)//下标从1开始
{
scanf("%d",&a[i]);//读取原数组
add(c[i],a);//对树状数组修改或赋值都用add函数,而不是简单相加
}2.按要求对某个点的值增加k
add(c[i],k);同样的,要用add函数对树状数组修改而不能直接修改
3.求某一区间和,并输出
ans=sum(r)-sum(l-1);
printf("%d\n",ans);这里要注意,sum(x)设计成返回区间[1,x]的值,如果要求区间[l,r]的和,就要用sum(r)-sum(l-1) 。
问题一解决,总时间复杂度O(NlogN),不会超时。
再来看第二个问题
有一个数组,多次往这个数组某个区间上的值增加k,再多次求某个点的值。
按照题意,事先编写的两个函数似乎不能满足需求,但事实上,利用差分的思想,在数据处理时稍作修改,就能在不改变两个核心函数的前提下求出答案。
差分: 差分数组中的某个元素b[i]为原数组对应元素与上一个元素之差a[i]-a[i-1]
设数组a[]=(1,2,4,1,1),那么差分数组b[]=(1,1,2,-3,0)
假设往原数组区间[2,4]加2
a[]=(1,4,6,3,1),差分数组就变成b[]=(1,3,2,-3,-2)
可以发现,差分数组只有b[2] (对应区间左端+k)和b[5] (对应区间右端+1处-k)变化了
进一步发现这时候再对差分数组求前x个和,对应的值就是当前x的值。
所以这时sum(x)不再是前x个数之和,而是原数组a[x]的值,即实现了单点查询
所以该类问题对区间[l,r]增加k,就要变为对c[l]处+k,对c[r+1]处-k,(当然,还是用add函数修改),再直接用sum(x)查询对应单点值,代码如下,问题二迎刃而解。
add(l,k);add(r+1,-k);
ans=sum(x);
printf("%d\n",ans);例题
在了解树状数组的原理、区间查询,单点更新和单点查询,区间更新的应用后,读者应当能够自行解决类似问题,这里先给出一些题
POJ 2299 Ultra-QuickSort (单点更新区间查询)
ZCMU1156 新年彩灯Ⅰ (区间更新单点查询)
HDU1556 Color the ball (区间更新单点查询)
留个坑
以上就是关于状数组的原理以及区间查询单点更新问题和单点查询区间更新问题的简单梳理,
树状数组还有其他高阶应用如多维树状数组、区间查询区间更新等问题,就在另外一篇博客见吧(逃