HDU 6521 Party（线段树 + 思维）

 

 

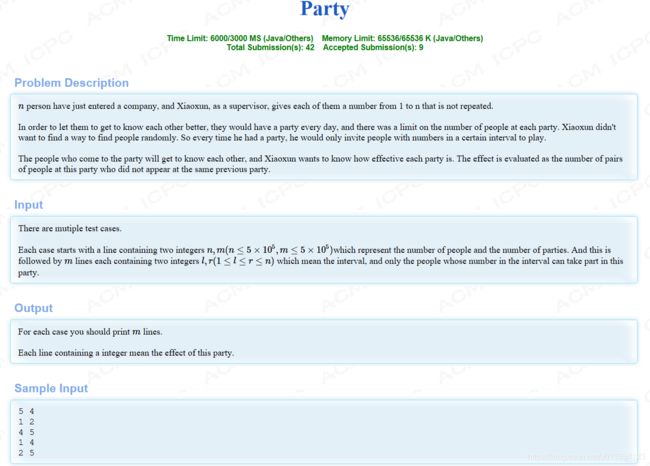
大致题意：有n个人，一开始相互不认识。他们要去参加party，每次参加的人是编号在区间[l,r]内的人。参加完一次party之后，这区间内的人就会相互认识。现在问你，每次参加party的时候，有多少对人会新认识。

首先，在参加这么多次party的过程中，每个人认识的人的编号显然是一个连续的区间。于是，我们就可以用L[i]和R[i]表示第i个人认识的人的区间左右端点。每次在参加party的过程中，我们实际上是要维护每一个人的L[i]和R[i]。

但是，直接维护显然是会超时的。我们考虑寻找一些性质，可以发现对于任意的j>i，一定有L[i]<=L[j]和R[i]<=R[j]。我们可以简单的证明一下：

          如果说L[i]>L[j]，那么说明j认识一个在i左边且i不认识的人x。而j要认识x，必然是在某次party中，x和j都参加了。对于这次party来说，x和j参加，那么必然i也参加，因为参加party是一个连续区间。所以i和x也相互认识，与条件i和x不认识矛盾。因此我们这条性质成立。

同理对于R[i]

根据这个性质，在任意时刻，L[i]和R[i]都是非严格单调递增的。所以对于每次开party的区间[l,r]，我们分成前后两个部分来求。对于前面的部分，我们可以尝试找到一个位置pos1使得在pos1之前的人认识的人的右端点小于r，也即在这一次party中，他们要认识后面的人。如此，这一部分要认识的人的对数就是：

                                                             

同理，对于后面部分，我们同样也可以找到一个pos2，使得在pos2之后的人认识的人的左端点大于l，也即在这次party中，他们要认识前面的人。相应的要认识的人的对数就是：

                                                           

这样我们就完成了计算。下面看如何维护L和R。在一次party之后，如果在此次之前认识的人的右端点已经大于r或者左端点已经小于l，那么对于的L和R就不用修改，我们需要修改的只是那些小于r和大于l的点。可以看到，我们还是可以利用刚刚提到的pos，相当于把[l,pos1]的所有R设置为r，把[pos2,r]的所有L设置为l。

 

总结一下，发现我们需要用一个可以快速求区间和，能够查找大于或者小于某个数的某个位置而且能够进行区间修改的数据结构。线段树是不错的选择。具体见代码：

#include 
#define INF 0x3f3f3f3f
#define LL long long
#define sc(x) scanf("%d",&x)
#define scc(x,y) scanf("%d%d",&x,&y)
#define sccc(x,y,z) scanf("%d%d%d",&x,&y,&z)

using namespace std;

const int N = 5e5 + 50;
const int mod = 1e9 + 7;

struct ST
{
    #define ls i<<1
    #define rs i<<1|1

	struct node
	{
		int max,min,lazy,l,r;
		LL sum;
	} T[N<<2];

	inline void push_up(int i)
	{
		T[i].sum=T[ls].sum+T[rs].sum;
		T[i].max=max(T[ls].max,T[rs].max);
		T[i].min=min(T[ls].min,T[rs].min);
	}

	void build(int i,int l,int r)
	{
		T[i]=node{0,0,0,l,r};
		if (l==r)
		{
			T[i].sum=T[i].max=T[i].min=l;
			return;
		}
		int mid=(l+r)>>1;
		build(ls,l,mid);
		build(rs,mid+1,r);
		push_up(i);
	}

	void push_down(int i)
	{
		T[ls].lazy=T[rs].lazy=T[i].lazy;
		T[ls].max=T[ls].min=T[i].lazy;
		T[rs].max=T[rs].min=T[i].lazy;
		T[ls].sum=(LL)(T[ls].r-T[ls].l+1)*T[i].lazy;
		T[rs].sum=(LL)(T[rs].r-T[rs].l+1)*T[i].lazy;
		T[i].lazy=0;
	}

	void update(int i,int l,int r,int x)
	{
		if ((T[i].l==l)&&(T[i].r==r))
		{
			T[i].sum=(LL)(r-l+1)*x;
			T[i].lazy=T[i].max=T[i].min=x;
			return;
		}
		if (T[i].lazy!=0) push_down(i);
		int mid=(T[i].l+T[i].r)>>1;
		if (mid>=r) update(ls,l,r,x);
		else if (mid>1;
		if (mid>=r) return getsum(ls,l,r);
		else if (midx) return T[i].l-1;
                else return T[i].l;
        }
        if (T[i].lazy!=0) push_down(i);
        if (T[ls].max<=x) query2(i<<1|1,x);
                        else query2(i<<1,x);
	}

	int query1(int i,int x)
	{
        if (T[i].l==T[i].r)
        {
            if (T[i].min=x) query1(i<<1,x);
                    else query1(i<<1|1,x);
	}

} seg1,seg2;


int main()
{
    int n,m;
    while(~scc(n,m))
    {
        seg1.build(1,1,n);
        seg2.build(1,1,n);
        while(m--)
        {
            int l,r;
            scc(l,r);
            LL ans=0;
            int pos=seg1.query1(1,l);
            if (pos<=r)
            {
                ans+=seg1.getsum(1,pos,r)-(LL)(r-pos+1)*l;
                seg1.update(1,pos,r,l);
            }
            pos=seg2.query2(1,r);
            if (pos>=l)
            {
                ans+=(LL)(pos-l+1)*r-seg2.getsum(1,l,pos);
                seg2.update(1,l,pos,r);
            }
            printf("%lld\n",ans/2);
        }
    }

}