机器学习 logistic回归的数学原理及Python简单实现

一、logistic回归的使用场景

在分类问题中，输出为离散值。如垃圾邮件过滤系统中，垃圾邮件预测值只能为是或否。线性回归适用于连续性变量的预测。而当添加一个新的与其他样本差异较大的样本时，回归曲线可能会变化较大。若输出值是离散的，要么0要么1，因此预测值很可能会剧烈变化，产生较大的误差。（连续变量变化不是太大，如从0.1变到0.2，但离散变量可能就从非垃圾邮件突然变垃圾邮件了，产生这个变化的原因仅仅是添加了一个差异较大的样本）因此通常情况分类问题不适合用线性回归拟合曲线。

二、logistic函数

分类问题的预测值不再适合用$h_{\theta }(x)$=${\sum }_{i=1}^{i=m}{\theta }_i{x}_i$。以输出值只有0和1为例，选取预测函数为$h_{\theta }(x)$=$\frac{1}{1+e^{-{\hat{\theta }}^{T}x}}$，此函数称为logistic函数，它的特点是当${\theta }^{T}x$很小时，函数值趋于0，当${\theta }^{T}x$ = 0时函数值为0.5，当${\theta }^{T}x$很大时函数值区域1。${\theta }^{T}x$=0称为拐点，在这一点函数斜率最大。由于预测值是离散的，而logistic函数也是连续的，因此往往使用一个阈值，超过阈值时为1，未超过时为0，比如把阈值设为0.5，logistic函数值大于0.5，输出值预测为1，小于则预测为0。logistic函数对于这类离散输出的分类问题具有较好的拟合性，函数值始终在(0,1)开区间内，可以有效避免一个差异较大的样本对模型造成的干扰

三、logistic回归

logistic函数的损失函数常常用概率的形式进行计算。由于P{Y_i=1}=$h_{\theta }(x_i)$，y_i只能取0或1，因此P{Y_i=0}=1-$h_{\theta }(x_i)$，用更简洁的写法就是P{Y_i=y_i}=$h_{\theta }(x_i{)}^{y_i}(1-h_{\theta }(x_i){)}^{1-y_i}$,y=0或1
则样本集的似然性函数L($\theta$)=${\prod }_{i=1}^{i=m}P${Y_i=y_i}=${\prod }_{i=1}^{i=m}{h}_{\theta }(x_i{)}^{y_i}(1-h_{\theta }(x_i){)}^{1-y_i}$，取对数后,ln(L($\theta$)) = ${\sum }_{i=1}^{i=m}$[$y_i\ast ln(h_{\theta }(x_i))+(1-y_i)ln(1-h_{\theta }(x_i)$]由概率论与数理统计中对样本参数选择的最大似然性法则可知，应选择似然性最大的参数$\hat{\theta }$
接下来，可以选择与梯度下降算法略有不同的梯度上升算法，即${\theta }_{i+1}$=${\theta }_i$+$\alpha ▽ln(L(\theta ))$来计算使得$ln(L(\theta ))$最大的参数$\theta$，然后根据计算出的参数$\theta$来计算检测点的预测值$h_{\theta }(x)$=$\frac{1}{1+e^{-{\hat{\theta }}^{T}x}}$。其中，$▽ln(L(\theta ))$=$[\frac{\partial ln(L(\theta ))}{\partial {\theta }_1}\ast \frac{{\hat{\theta }}_1}{|{\hat{\theta }}_1|},\frac{\partial ln(L(\theta ))}{\partial {\theta }_2}\ast \frac{{\hat{\theta }}_2}{|{\hat{\theta }}_2|},...\frac{\partial ln(L(\theta ))}{\partial {\theta }_n}\ast \frac{{\hat{\theta }}_n}{|{\hat{\theta }}_n|}{]}^T$ ,而$\frac{\partial ln(L(\theta ))}{\partial {\theta }_j}$化简后等于${\sum }_{i=1}^{i=m}(y_i-h_{\theta }(x_i))x_{ij}$ ，由此，logistic回归的预测函数$h_{\theta }(x_i)$=$\frac{1}{1+e^{-{\hat{\theta }}^{T}x}}$与损失函数$J(\theta )$=ln(L($\theta$)) = ${\sum }_{i=1}^{i=m}$[$y_i\ast ln(h_{\theta }(x_i))+(1-y_i)ln(1-h_{\theta }(x_i)$]以及梯度公式均已得到。

四、一个简单的logistic回归预测

选择正态分布的二维特征进行回归预测

import numpy as np
import math
#用logistic计算h_\theta(x)
def sigmoid(inX):
    return 1.0/(1+math.exp(-inX))
#生成数据
y1_x1_mu,y1_x1_sigma = 0,3#分类结果为1的y的x1的均值和方差
y1_x1 = np.random.normal(y1_x1_mu,y1_x1_sigma,20)#正态分布中取20个随机数
y1_x2_mu,y1_x2_sigma = 1,2#分类结果为1的y的x2的均值和方差
y1_x2 = np.random.normal(y1_x2_mu,y1_x2_sigma,20)
y1 = np.ones((20,1))

y0_x1_mu,y0_x1_sigma = 0,2#分类结果为0的y的x1的均值和方差
y0_x1 = np.random.normal(y0_x1_mu,y0_x1_sigma,20)
y0_x2_mu,y0_x2_sigma = 5,3
y0_x2 = np.random.normal(y0_x2_mu,y0_x2_sigma,20)
y0 = np.zeros((20,1))

x1 = list(y1_x1)#将y1_x1转为列表 方便合并
x1.extend(list(y0_x1))#在列表末尾添上另一个列表（合并）
x2 = list(y1_x2)
x2.extend(list(y0_x2))
y = list(y1)
y.extend(list(y0))

#梯度上升进行训练，得到合适的参数
#已有m=40个x1,x2,和y，前20个是y1后20个是y0
def gradAdcent(x1,x2,y):
    if len(x1)!=40 or len(x2)!=40 or len(y)!=40:
        print('parameter number error,it should be 40')
        return 
    loss = 1
    theta = [0,0]#2*1
    step_size = 0.01#步长,alpha
    iter_count = 0
    max_iters = 100
    while iter_count < max_iters:
        loss = 1#似然性
        gradient_0 = 0#第一维的梯度分量
        gradient_1 = 0#第二维的梯度分量
        #计算第一维的梯度分量
        for i in range(0,40):
            h_theta = sigmoid(x1[i]*theta[0]+x2[i]*theta[1])
            gradient_0 += (y[i]-h_theta)*x1[i]
        #计算第二维梯度分量
        for i in range(0,40):
            h_theta = sigmoid(x1[i]*theta[0]+x2[i]*theta[1])
            gradient_1 += (y[i]-h_theta)*x2[i]
        #沿梯度方向上升
        theta[0] += step_size*gradient_0
        theta[1] += step_size*gradient_1
        #计算似然性
        for i in range(0,40):
            h_theta = sigmoid(x1[i]*theta[0]+x2[i]*theta[1])#h_theta(xi)
            if y[i] != 1 and y[i] != 0:
                print('data error of y',(i+1),'it should be 1 or 0')
                return 
            if y[i] ==1 :
                loss *= h_theta
            if y[i] ==0 :
                loss *= (1-h_theta)           
        iter_count += 1
        print('iter_count',iter_count)
        print('theta:',theta)
        print('loss',loss)
    return theta
print('x1:',x1)
print('x2:',x2)
print('y:',y)
#进行训练
final_theta = gradAdcent(x1=x1,x2=x2,y=y)
print('final_theta:',final_theta)
#进行预测
#生成10个预测结果应为1的测试数据，再生成10个预测结果应为0的测试数据.
test_y1_x1 = np.random.normal(y1_x1_mu,y1_x1_sigma,10)
test_y1_x2 = np.random.normal(y1_x2_mu,y1_x2_sigma,10)
test_y0_x1 = np.random.normal(y0_x1_mu,y0_x1_sigma,10)
test_y0_x2 = np.random.normal(y0_x2_mu,y0_x2_sigma,10)
test_x1 = list(test_y1_x1)
test_x1.extend(test_y0_x1)
test_x2 = list(test_y1_x2)
test_x2.extend(test_y0_x2)
right_count = 0
#前十项为预测结果为1的x1,x2，后十项为预测结果为0的x1,x2
#logistic预测值大于0.5预测为1，小于0.5预测为0
for i in range (0,10):
    h_theta = sigmoid(test_x1[i]*final_theta[0]+test_x2[i]*final_theta[1])
    if h_theta >= 0.5:
        right_count += 1
for i in range (0,10):
    h_theta = sigmoid(test_x1[i]*final_theta[0]+test_x2[i]*final_theta[1])
    if h_theta <= 0.5:
        right_count += 1
print('right_count:',right_count)
print('accurate rate:',(right_count/20))
print('end')

运行结果如下

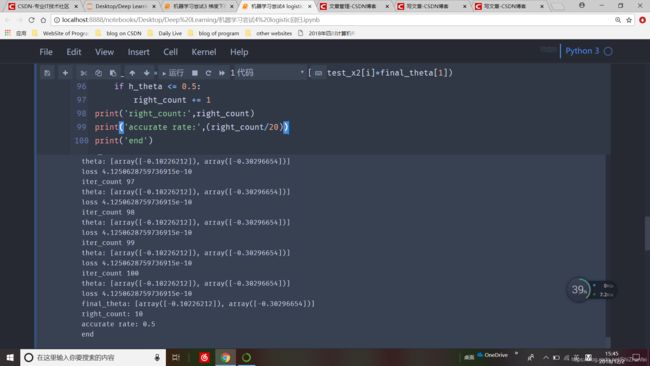
所选参数大致能得到预测准确率稳定在50%左右的训练模型。本文重点在于logistic回归数理过程的梳理和算法实现原理，等知识水平提高，经验丰富后，应该能得到更好的模型。

2018/12/2