R语言入门（1）时间序列分析

时间序列分析

---

使用软件为Rstudio，参考CRAN中时间序列分析分析函数和package，拿手上的数据练习一下时间序列分析。

1、原始数据说明

选择连续9天的数据，共2025条，时间间隔为5分钟。具体情况如下：

2、平稳性检验

所谓平稳，是指因变量围绕着一个常数上下波动。更学术一点，就是是说统计特性（mean，variance，correlation等）不会随着时间窗口的不同而变化。

2.1 时间序列可视化

因为一些高阶函数可能不能准确地产生我想要的图，所以我这里用的是低阶图形命令手动设置label。首先把plot()函数里的默认坐标轴关掉：xaxt='n'，然后通过axis()函数手动添加坐标轴。代码如下：

plot(indata,type = "s",xaxt='n',xlab = "time")
axis(1,c(1,226,451,676,901,1126,1351,1576,1801),c('5:00','5:00','5:00','5:00','5:00','5:00','5:00)

生成图形如下：

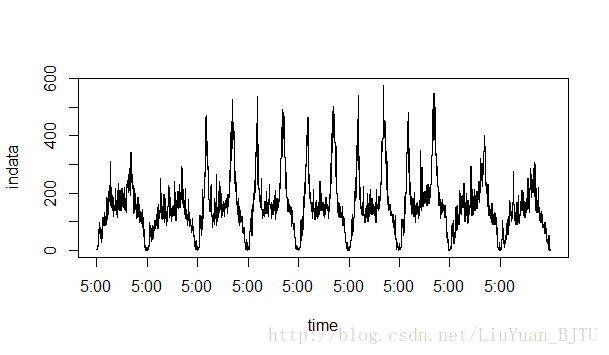
由上图可知：
1. 该时间序列存在很强的周期性
2. 该时间序列是平稳的。
还可以用xts函数把原始数据转换成时间序列，也就是把给每个数据对应上一个时间点，代码如下

data_1<-xts(indata_1,seq(ISOdate(0, 0, 0, 5, 0, 0),ISOdate(0, 0, 0, 23, 40, 0),by="5 mins"))
plot(data_1)

进一步绘制每一天的箱型图，代码如下：

library(ggplot2)
ggplot(data,aes(x=factor(STATDATE),y=INDATA)) + geom_boxplot()

由上图可知：

1. 周末的异常点较少，平日的异常点较多，说明平日存在高峰情况。

2.2 自相关和偏自相关图

此外，还可以通过自相关和偏自相关图来判断时间序列是否平稳。平稳的序列的自相关图和偏相关图不是拖尾就是截尾。截尾是指在某阶之后，系数都为 0；拖尾是指有一个衰减的趋势，但是不都为0。

ACF形状	模型
不衰减到0	不平稳
固定点上有大于0的值（周期性）	周期性
所有点都是0	完全随机（白噪声）
指数衰减到0（拖尾）	AR(p)
正负交替衰减到0（拖尾）	AR(p)
前几个大于0，后面都为0（截尾）	MA(q)

绘制采用R中acf(indata)函数（默认滞后30阶）的自相关图和偏自相关图如下：

由上图可知：

1. 自相关图逐渐衰减到0，存在拖尾性，偏自相关图在5阶后都为0，存在截尾性。说明该时间序列在短期内（30阶）是平稳时间序列。

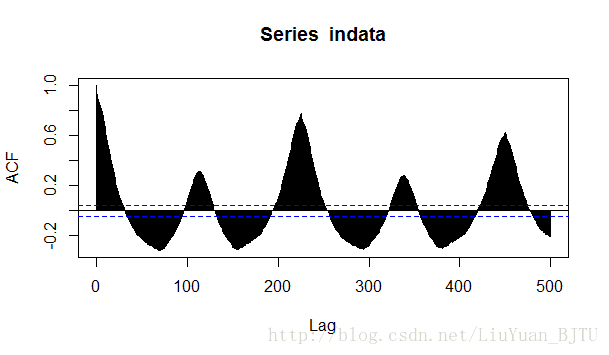
考虑到滞后阶数为30，而该原始数据的周期性可能要到225阶以后才能体现出来。设置自相关图的滞后阶数为500，代码如下：

acf(indata,lag=500)
pacf(indata,lag=500)

2.3 ADF单位根平稳型检验

单位根检验是指检验序列中是否存在单位根，因为存在单位根就是非平稳时间序列了。[百度百科]
此处使用tseries包中的adf.test()函数对9天数据进行单位根平稳性检验，结果如下：

> adf.test(indata)

    Augmented Dickey-Fuller Test

data:  indata
Dickey-Fuller = -7.1486, Lag order = 12, p-value = 0.01
alternative hypothesis: stationary

aternative hypothesis称为备择假设，与原假设相对。这里备择假设是该时间序列平稳。因为p值小于0.05，拒绝原假设，接受备择假设，所以说明该时间序列是平稳的。
有意思的是，我单独拿一天的数据出来做单位根检验，可以发现该时间序列并不平稳。

> adf.test(indata_1)

    Augmented Dickey-Fuller Test

data:  indata_1
Dickey-Fuller = -1.0092, Lag order = 6, p-value = 0.9351
alternative hypothesis: stationary

3、时间序列模型选择

3.1 常用的时间序列模型

下面简单介绍下常用的时间序列模型：

1. 移动平均（MA, moving average）
   MA(1):
   Yt=α0+α1ut−1+ut
   
   MA(q):
   Yt=α0+α1ut−1+...+αqut−q+ut

2. 自回归模型（AR, Auto regresstion）
   AR(1):

   Yt=β0+β1Yt−1+ut
   
   AR(p):
   Yt=β0+β1Yt−1+...+βpYt−p+ut

3. 自回归移动平均（ARMA）
   ARMA(p, q):

   Yt=β0+β1Yt−1+...+βpYt−p+α1ut−1+...+αqut−q+ut

4. 差分自回归移动平均（ARIMA）
   观测时间序列是否为平稳。若为平稳序列，则用ARMA(p,q)模型；若为非平稳时间序列，则要先进行d阶差分运算后化为平稳时间序列，此处的d即为ARIMA(p,d,q)模型中的d。

3.2 时间序列模型选择

自相关和偏自相关检验：
因为平稳的序列的自相关图和偏相关图不是拖尾就是截尾，所以可根据自相关和偏自相关图的截尾和拖尾来选择时间序列模型。

模型	ACF	PACF
AR(p)	衰减趋于零(拖尾)	p阶后截尾
MA(q)	q阶后截尾	衰减趋于零（拖尾）
ARMA(p, q)	q阶后衰减趋于零（拖尾）	p阶后衰减趋于零（拖尾）

若都拖尾，得到ARMA(p，q)模型，自相关图有几个在两倍标准差之外就能确定p，偏自相关图突出两倍标准差的确定q。可用AIC和SBC准则判断得到的p和q参数值的好坏，这两个指标越小越好。
所幸，R语言的forecast包中提供的auto.arima()函数可以自动找到最优的p，q值，代码如下：

> library(forecast)
> auto.arima(indata,trace = T)

 ARIMA(2,0,2) with non-zero mean : 20160.45
 ARIMA(0,0,0) with non-zero mean : 24296.42
 ARIMA(1,0,0) with non-zero mean : 20279.09
 ARIMA(0,0,1) with non-zero mean : 22583.28
 ARIMA(0,0,0) with zero mean     : 26869.16
 ARIMA(1,0,2) with non-zero mean : 20157.5
 ARIMA(1,0,1) with non-zero mean : 20169.87
 ARIMA(1,0,3) with non-zero mean : 20159.35
 ARIMA(2,0,3) with non-zero mean : 20161.85
 ARIMA(1,0,2) with zero mean     : Inf
 ARIMA(0,0,2) with non-zero mean : 21739.44

 Best model: ARIMA(1,0,2) with non-zero mean 

Series: indata 
ARIMA(1,0,2) with non-zero mean 

Coefficients:
         ar1      ma1      ma2      mean
      0.9711  -0.2664  -0.0793  154.5767
s.e.  0.0058   0.0228   0.0208   17.3612

sigma^2 estimated as 1229:  log likelihood=-10075.54
AIC=20161.08   AICc=20161.11   BIC=20189.15

参数	含义
s.e.(SE)	系数的标准差
sigma^2 estimated	估计值方差
log likelihood	对数似然值

还可以用summary()函数对拟合结果进行描述统计，计算一些误差（Training set error measures:）。

> summary(auto.arima(indata))
Series: indata 
ARIMA(1,0,2) with non-zero mean 

Coefficients:
         ar1      ma1      ma2      mean
      0.9711  -0.2664  -0.0793  154.5767
s.e.  0.0058   0.0228   0.0208   17.3612

sigma^2 estimated as 1229:  log likelihood=-10075.54
AIC=20161.08   AICc=20161.11   BIC=20189.15

Training set error measures: ME     RMSE     MAE  MPE MAPE      MASE          ACF1
Training set：0.03822178 35.02654 25.4774 -Inf  Inf 0.9615727 -2.066828e-05

参数	含义
ME	Mean Error
RMSE	Root Mean Squared Error
MAE	Mean Absolute Error
MPE	Mean Percentage Error
MAPE	Mean Absolute Percentage
MASE	Mean Absolute Scaled Error

从上述结果可以看出，用来拟合这九天最优的模型是ARIMA(1,0,2) with non-zero mean。with non-zero mean是指常数项不为0，因此我们可以写出该ARIMA模型的公式，如下：

Yt=154.5767+0.9711×Yt−1−0.2664×ut−1−0.0793×ut−2+ut

其中 ut 、 ut−1 、 ut−2 都服从正态分布。

3.3 用模型来预测

在选择好模型后，我们可以使用该模型来做一些预测，例如预测未来一天（225个时段）的数据，代码如下：

fit<-auto.arima(indata)
forecast <- forecast.Arima(fit,h=225,level=c(99.5))
plot.forecast(forecast)

图1 预测未来225个时段（1天）

图2 预测未来7个时段
由图1和图2可知，ARIMA模型仅能适用于短期的预测（7个时段），不能使用于长期的预测（225个时段）。