R语言-相关
相关系数是可以用来描述定量变量之间的关系。相关系数的符号（
）是表明关系的方向（正相关或负相关），其值（绝对值）大小表示关系的强弱程度（完全不相关时为0，完全相关时为1）。
一。相关的类型
1.Pearson、Spearman和Kendall相关
- Pearson积差相关系数衡量了两个定量变量之间的线性相关程度
- Spearman等级相关系数衡量分级定序变量之间的相关程度，又称为秩相关系数。利用两变量的大小作线性相关分析，对原始变量的分布不做要求，属于非参数统计方法。其适用范围比Pearson相关系数要广得多。
- Kendall等级相关系数是用于反映分类变量相关性的指标，适用于两个变量均为有序分类的情况。
注：
- 定量变量 也就是通常所说的连续量，如长度、重量、产量、人口、速度和温度等，它们是由测量或计数、统计所得到的量，这些变量具有数值特征，称为定量变量。
- 定性变量 这些量并非真有数量上的变化，而只有性质上的差异。这些量还可以分为两种，一种是有序变量，它没有数量关系，只有次序关系，如某种产品分为一等品、二等品、三等品等，矿石的质量分为贫矿和富矿；另一种是名义变量，这种变量既无等级关系，也无数量关系，如天气（阴、晴）、性别（男、女）、职业（工人、农民、教师、干部）和产品的型号等。
- 有序分类变量（ordinal categorical variable）是统计学中，根据取值特征而分类的一种定性变量。所谓有序分类变量，是指其取值的各类别之间存在着程度上的差别，给人以“半定量”的感觉，因此也称为等级变量，如学历（文盲、小学、初中、高中、大学、研究生等）
- 定序变量能决定次序，也即变量的值能把研究对象排列高低或大小，具有>与<的数学特质。它是比定类变量层次更高的变量，因此也具有定类变量的特质，即区分类别（=，≠）。例如文化程度可以分为大学、高中、初中、小学、文盲；工厂规模可以分为大、中、小；年龄可以分为老、中、青。这些变量的值，既可以区分异同，也可以区别研究对象的高低或大小。但是，各个定序变量的值之间没有确切的间隔距离。比如大学究竟比高中高出多少，大学与高中之间的距离和初中与小学之间的距离是否相等，通常是没有确切的尺度来测量的。
- 定量变量也就是通常所说的连续量，如长度、重量、产量、人口、速度和温度等，它们是由测量或计数、统计所得到的量，这些变量具有数值特征，称为定量变量。
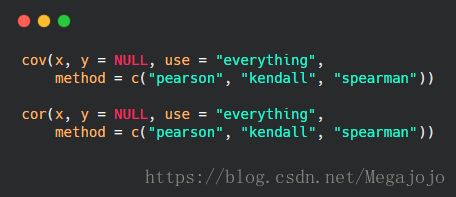
cor()函数可以计算这三种相关系数，cov()函数可以用来计算协方差。
- x,y：矩阵或数据框（对var()函数来说还可以是数字向量）
- use：指定缺失数据的处理方式。可选的方式有all.obs（遇到确实数据时将报错）、everything（遇到缺失数据时，相关系数的计算结果被设为missing，默认）、complete.obs（行删除）以及pairwise.complete.obs（成对删除）
- method：指定相关系数的类型。可选为pearson（默认）、spearman、kendall
2.偏相关
概念：某一个要素对另一个要素的影响或相关程度时，把其他要素的影响视为常数，即暂不考虑其他要素的影响，而单独研究那两个要素之间的 相互关系的密切程度时，称为偏相关。
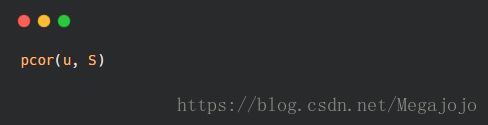
ggm包中的pcor()函数计算偏相关系数：
- u：向量，可以是数值型向量（每个数字代表变量的下标），也可以是字符型向量，包含变量的变量名。前两个数值/变量名是要计算相关系数的下标/要计算相关系数变量的变量名，其余都为条件变量（即要排除影响的变量）下标/变量名
- S：变量的协方差矩阵
> library(ggm)
> pcor(c(1, 5, 2, 3, 6), cov(states)) #计算下标为1和5的偏相关系数
[1] 0.3462724
> colnames(states)
[1] "Population" "Income" "Illiteracy" "Life Exp" "Murder" "HS Grad"
> pcor(c("Population", "Murder", "Income", "Illiteracy", "HS Grad"), cov(states))
[1] 0.3462724二。相关性的显著性验证
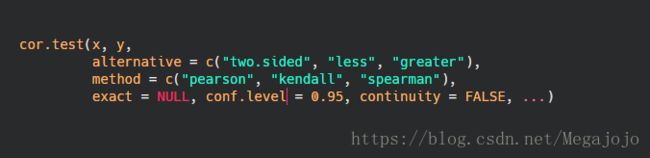
常用的原假设为变量间不相关（即总体的相关系数为0），可以用cor.test()函数对单个Pearson、Spearman和Kendall相关系数进行检验。
- x,y：为要检验相关性的变量
- alternative：用来指定双侧检验或单侧检验（取值为“two.side"、"less"（研究的假设为总体的关系系数小于0）或"greater"（研究的假设为总体的关系系数大于0））
- exact：是否计算精准p值，用于Spearman和Kendall相关系数检验；
- conf.level：置信度，目前只用于Pearson相关系数检验
- continuity：TRUE时，Spearman和Kendall的值不会被精准计算（？）
关于双侧检验与单侧检验
1.双侧检验也叫双尾检验，目的在于判断有无差异，而不考虑谁大谁小。原假设H0：u1=u2，即二者之间无差异
2.单侧检验要考虑大小，greater时，即已知u1不会小于u2，故原假设H0：u1
u2；less时，即已知u1不会大于u2，则原假设H0：u1
u2
应用举例：
1.一般若事先不知道所比较的两个处理谁好谁坏，分析的目的在于推断两个处理效果有无差别，则选用双侧检验（一般情况下，如不作特殊说明均指双侧检验）：两种药物分别处理芽殖酵母，比较芽殖酵母存活寿命；
2.若根据理论知识或实践经验判断甲处理效果不会比乙处理的效果差（好），分析的目的在于推断甲处理比乙处理好（差），则单侧检验：改进新技术后，已知这个技术不会降低生产量，那么与原技术的比较检验，则应采用greater。
> cor.test(states[, 3], states[, 5])
Pearson's product-moment correlation
data: states[, 3] and states[, 5]
t = 6.8479, df = 48, p-value = 1.258e-08
alternative hypothesis: true correlation is not equal to 0
95 percent confidence interval:
0.5279280 0.8207295
sample estimates:
cor
0.7029752psych包中corr.test()函数可以为pearson、spearman、kendall计算相关矩阵和显著性水平。
- x,y：矩阵或数据框，二者具有相同行数
- adject：多态检验的校正方法（"holm", "hochberg", "hommel", "bonferroni", "BH", "BY", "fdr", "none"），相对于bonferroni来说，优先使用holm
- alpha：置信水平
- ci：默认情况下，会找出置信区间
> library(psych)
> corr.test(states, use = "complete")
Call:corr.test(x = states, use = "complete")
Correlation matrix
Population Income Illiteracy Life Exp Murder HS Grad
Population 1.00 0.21 0.11 -0.07 0.34 -0.10
Income 0.21 1.00 -0.44 0.34 -0.23 0.62
Illiteracy 0.11 -0.44 1.00 -0.59 0.70 -0.66
Life Exp -0.07 0.34 -0.59 1.00 -0.78 0.58
Murder 0.34 -0.23 0.70 -0.78 1.00 -0.49
HS Grad -0.10 0.62 -0.66 0.58 -0.49 1.00
Sample Size
[1] 50
Probability values (Entries above the diagonal are adjusted for multiple tests.)
Population Income Illiteracy Life Exp Murder HS Grad
Population 0.00 0.59 1.00 1.0 0.10 1
Income 0.15 0.00 0.01 0.1 0.54 0
Illiteracy 0.46 0.00 0.00 0.0 0.00 0
Life Exp 0.64 0.02 0.00 0.0 0.00 0
Murder 0.01 0.11 0.00 0.0 0.00 0
HS Grad 0.50 0.00 0.00 0.0 0.00 0
To see confidence intervals of the correlations, print with the short=FALSE option关于偏相关的显著性检验（未测试）
ggm包中pcor.test()函数可以用来检验在控制一个或多个额外变量时两个变量之间的条件独立性。
- r：由pcor()函数计算得到的偏相关系数
- q：要控制的变量数（以数值表示位置）
- n：为样本大小
MARK一下r.test，有空再看