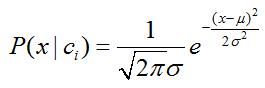机器学习 - 朴素贝叶斯

朴素贝叶斯是基于贝叶斯定理与条件独立假设的分类方法。对于给定的训练数据，首先基于特征条件独立假设学习联合概率分布p(X, ci) = p(X|ci)p(ci)，即朴素贝叶斯核心公式的分子。朴素贝叶斯就两个东西：训练出词概率向量（任意一个类别中，每个单词出现的概率）即条件概率，类别概率即先验。只要我们训练出了这两个东西，那么后面无论给出什么样的样本的词向量，我们都能轻松算出这个词向量属于每个类别的概率。

1. 朴素贝叶斯的核心公式

朴素贝叶斯要解决的问题是将train_x与tran_y进行训练，然后对test_x进行分类。设X是test_x中任意一个样本，xi是X的任意一个特征，xi之间条件独立；ci是分类的label，如二分类的0/1。则有下列公式：

我们要想对X进行分类，则需要计算出所有的p(ci|X)，然后比较哪一个最大，则X属于哪一类。因此就是计算p(X|ci)，p(ci)，p(X)；由于p(X)为全概率，不用进行计算。故需要计算p(X|ci)，p(ci)；p(ci)为先验概率刻画是的类别ci发生的可能性，p(X|ci)为条件概率，即在类别ci中X出现的概率，因为特征条件独立，因此p(X|ci)，为X中各个特征出现的概率的乘积。把p(x1|ci)，p(x2|ci)...p(xn|ci)放入到一个向量中，就是训练生成的词概率向量。p(ci)为每个类别的概率，很容易在训练过程中计算出来；p(X|ci) 可以先通过训练集训练出一个词概率向量，比如[0.1, 0.2, 0.15, 0.15, 0.3，0.1]来代表类别ci中每个特征/单词出现的概率（需要使用拉普拉斯平滑，避免词概率向量中出现0）。然后预测时使用X的词向量如[0, 0, 1, 1, 0，2]，p(X|ci) = (1 * 0.15) * (1 * 0.15) * (2* 0.1) = 0.0045。

2. 代码实现

# -*- coding: utf-8 -*-
""" naive bayes
本程序实现了朴素贝叶斯算法; 整个程序主要分为三部分: 生成可训练数据, 训练模型, 预测

生成可训练数据: 
    1. load_data: 导入train_data, label
    2. setOfWord: 将train_data中所有单词汇集到一个词集, 生成一个词集列表wordSet
    3. create_wordVec: 将一个样本转化为一个词向量, 可以使用词集模型(wordSet)或者词袋模型(wordBag)
    4. 将生成的词向量拼接, 形成可训练数据
    
训练模型
    1. train_NB: 训练naive bayes模型, 目标求出四个变量: 类别0的词概率向量, 类别1的词概率向量, 
    类别0的概率, 类别1的概率。probability_0, probability_1, p_spam(因为是2分类, 故另一个就是1-p_spm);
    在计算概率时要进行拉普拉斯平滑
    
预测
    1. 将被预测样本生成词向量
    2. predict
"""
import numpy as np


def load_data():
    """ 1. 导入train_x, train_y """
    train_data = [["my", "dog", "has", "flea", "problems", "help", "please"],
                  ["maybe", "not", "take", "him", "to", "dog", "park", "stupid"],
                  ["my", "dalmation", "is", "so", "cute", "I", "love", "him"],
                  ["stop", "posting", "stupid", "worthless", "garbage"],
                  ["him", "licks", "ate", "my", "steak", "how", "to", "stop", "him"],
                  ["quit", "buying", "worthless", "dog", "food", "stupid"]]
    label = [0, 1, 0, 1, 0, 1]
    return train_data, label


def setOfWord(train_data):
    """ 2. 所有单词不重复的汇总到一个列表 
    train_data: 文档合集, 一个样本构成一个文档
    wordSet: 所有单词生成的集合的列表
    """
    wordList = []
    
    length = len(train_data)
    for sample in range(length):
        wordList.extend(train_data[sample])
    wordSet = list(set(wordList))
    return wordSet


def create_wordVec(sample, wordSet, mode="wordSet"):
    """ 3. 将一个样本生成一个词向量 """
    length = len(wordSet)
    wordVec = [0] * length

    if mode == "wordSet":
        for i in range(length):
            if wordSet[i] in sample:
                wordVec[i] = 1
    elif mode == "wordBag":
        for i in range(length):
            for j in range(len(sample)):
                if sample[j] == wordSet[i]:
                    wordVec[i] += 1
    else:
        raise(Exception("The mode must be wordSet or wordBag."))
    return wordVec


def train_NB(train_x, train_y):
    """ 5. 训练naive bayes, 必须2分类问题 """
    category = 2
    feaNum = len(train_x[0])
    sampleNum = len(train_y)
    probability_1, probability_0 = np.ones((feaNum,)), np.ones((feaNum,))
    class0_num, class1_num = category, category
    
    p_spam = sum(train_y) / len(train_y)
    
    for sample in range(sampleNum):
        if train_y[sample] == 0:
            probability_0 = probability_0 + train_x[sample]
            class0_num = class0_num + sum(train_x[sample])
        elif train_y[sample] == 1:
            probability_1 = probability_1 + train_x[sample]
            class1_num = class1_num + sum(train_x[sample])
        else:
            raise(Exception("The lables must be 0, 1."))
    
    probability_0 = probability_0 / class0_num
    probability_1 = probability_1 / class1_num
    return probability_0, probability_1, p_spam


def predict(p0, p1, p_spam, test_x):
    """ 6. 预测test_x """
    P0, P1 = 1.0, 1.0
    
    length = len(test_x)
    for i in range(length):
        # 如果词向量太长, 可以取对数, 用加法代替乘法, 同时防止下溢
        if test_x[i] == 1:
            P0 = P0 * (test_x[i] * p0[i])
            P1 = P1 * (test_x[i] * p1[i])
            
    P0 = P0 * (1 - p_spam)
    P1 = P1 * p_spam
    
    if P0 > P1:
        return P0, P1, 0
    else:
        return P0, P1, 1


def main(test_data, mode="wordSet"):
    # 1. load data
    train_x, label = load_data()
    
    # 2. 生成词集
    wordSet = setOfWord(train_x)
    print("训练集生成的词集为: {0}".format(wordSet))
    
    # 3. 生成可训练数据
    sampleCnt = len(train_x)
    train_matrix = []
    for i in range(sampleCnt):
        train_matrix.append(create_wordVec(train_x[i], wordSet, mode))
    print("训练集生成的可训练数据为: {0}".format(train_matrix))
        
    # 4. 训练naive bayes模型
    p0, p1, p_spam = train_NB(train_matrix, label)
    print("类别0的词概率向量为: {0}".format(p0))
    print("类别0的概率为: {0}".format(1-p_spam))
    print("类别1的词概率向量为: {0}".format(p1))
    print("类别1的概率为: {0}".format(p_spam))
    
    # 5. 生成测试数据
    test_x = create_wordVec(test_data, wordSet)
    print("测试数据为: {0}".format(test_data))
    print("测试集生成的可训练数据为: {0}".format(test_x))
    
    # 6. 预测
    P0, P1, prediction = predict(p0, p1, p_spam, test_x)
    print("类别0的概率值为: {0}, 类别1的概率值为: {1}".format(P0, P1))
    
    if prediction == 1:
        print("当前文档为垃圾邮件.")
    else:
        print("当前文档为非垃圾邮件.")
    return test_x
        

if __name__ == "__main__":
    p0 = main(["stupid", "dog"], "wordSet")
    
    
    """
    1. 训练数据 & 每个样本的label：
    [["my", "dog", "has", "flea", "problems", "help", "please"],
     ["maybe", "not", "take", "him", "to", "dog", "park", "stupid"],
     ["my", "dalmation", "is", "so", "cute", "I", "love", "him"],
     ["stop", "posting", "stupid", "worthless", "garbage"],
     ["him", "licks", "ate", "my", "steak", "how", "to", "stop", "him"],
     ["quit", "buying", "worthless", "dog", "food", "stupid"]]
    [0, 1, 0, 1, 0, 1]
    
    2. 训练数据生成的单词集合：
    [help, licks, food, stupid, steak, is, flea, ate, love, dog, not, garbage, 
     maybe, buying, cute, please, posting, to, worthless, has, him, take, quit, 
     I, problems, park, stop, so, how, my, dalmation]
    
    3. 训练数据生成的词向量：
    [[1, 0, 0, 0, 0, 0, 1, 0, 0, 1, 0, 0, 0, 0, 0, 1, 0, 0, 0, 1, 0, 0, 0, 0, 1, 0, 0, 0, 0, 1, 0]
     [0, 0, 0, 1, 0, 0, 0, 0, 0, 1, 1, 0, 1, 0, 0, 0, 0, 1, 0, 0, 1, 1, 0, 0, 0, 1, 0, 0, 0, 0, 0]
     [0, 0, 0, 0, 0, 1, 0, 0, 1, 0, 0, 0, 0, 0, 1, 0, 0, 0, 0, 0, 1, 0, 0, 1, 0, 0, 0, 1, 0, 1, 1]
     [0, 0, 0, 1, 0, 0, 0, 0, 0, 0, 0, 1, 0, 0, 0, 0, 1, 0, 1, 0, 0, 0, 0, 0, 0, 0, 1, 0, 0, 0, 0]
     [0, 1, 0, 0, 1, 0, 0, 1, 0, 0, 0, 0, 0, 0, 0, 0, 0, 1, 0, 0, 1, 0, 0, 0, 0, 0, 1, 0, 1, 1, 0]
     [0, 0, 1, 1, 0, 0, 0, 0, 0, 1, 0, 0, 0, 1, 0, 0, 0, 0, 1, 0, 0, 0, 1, 0, 0, 0, 0, 0, 0, 0, 0]]
    
    4. 类别0的词概率向量, 类别0的概率; 类别1的词概率向量, 类别1的概率：
    [****]: (31个元素, 其中每个元素代表当前单词在该类别中出现的概率)
    0.5
    朴素贝叶斯公式的分子, 也是朴素贝叶斯的核心
    
    5. 测试集数据 & 测试集生成的词向量
    ["stupid", "dog"]
    [0, 0, 0, 1, 0, 0, 0, 0, 0, 1, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0]
    
    6. 预测
    """

3. 朴素贝叶斯处理重复单词

3.1 多项式模型

即词袋模型，出现几次就记为几。

3.2 伯努利模型

即词集模型，只考虑出不出现。

4. 朴素贝叶斯的应用场景

1）文本分类，垃圾邮件过滤，文本主题判断。

2）文本相关多分类实时预测。

3）推荐系统，朴素贝叶斯 + 协同过滤

5. 朴素贝叶斯优缺点

5.1 优点

1）简单，快速。比如反垃圾邮件中，就是将被预测样本的词向量与训练好的概率向量相乘。

2）对于标称型特征，效果非常好；对于数值型特征，我们默认他是服从正态分布的（效果难以保证）。

5.2 缺点

1）朴素贝叶斯有特征独立同分布的假设。

2）拉普拉斯平滑。

3）没有考虑词语之间的顺序，“朴素贝叶斯”与“贝叶斯朴素完全一样”，而rnn等更高级的算法则会考虑到这些性质。

4）输出的概率值无实际意义，仅供比较大小。

6. 数值型数据如何处理？

朴素贝叶斯的核心就是计算先验概率，条件概率；对于标称型数据而言这是比较容易的。但是数值型数据呢，怎么计算条件概率？

1）对数据取对数，或者取倒数，使其更加符合正态分布；

2）将数据当做正态分布，计算每个类别的均值和方差；

3）计算条件概率：

7. 使用注意事项

1）当特征是数值型特征时，要对其进行调整，想办法使这个特征满足正态分布。

2）拉普拉斯平滑。