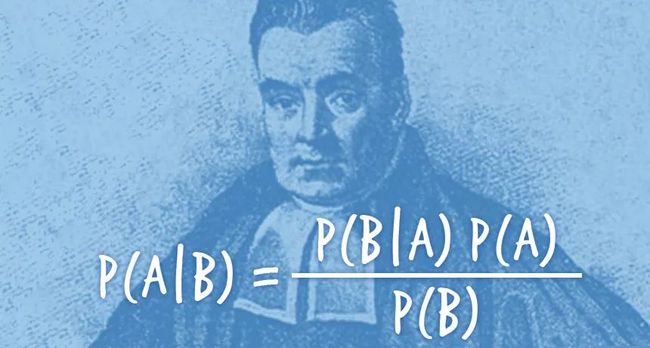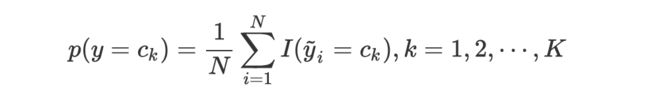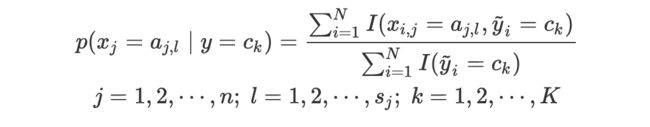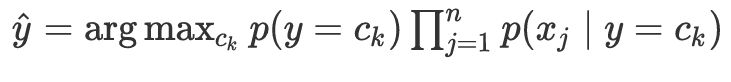【机器学习基础】数学推导+纯Python实现机器学习算法11：朴素贝叶斯

Python机器学习算法实现

Author：louwill

     

     今天要讲的算法是朴素贝叶斯(Naive Bayes)。相较于之前的支持向量机等模型，朴素贝叶斯就要简单多了。朴素贝叶斯是一种基于贝叶斯定理和特征条件独立假设的分类算法。

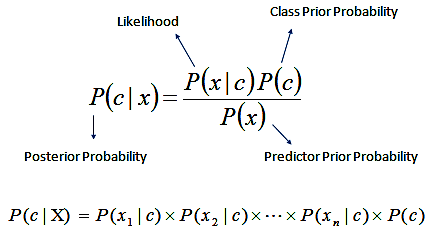
     简单而言，对于给定的训练数据，朴素贝叶斯先基于特征条件独立假设学习输入和输出的联合概率分布，然后基于此分布对于新的实例，利用贝叶斯定理计算出最大的后验概率。朴素贝叶斯不会直接学习输入输出的联合概率分布，而是通过学习类的先验概率和类条件概率来完成。

     所谓朴素贝叶斯中朴素的含义，即特征条件独立假设，条件独立假设就是说用于分类的特征在类确定的条件下都是条件独立的。这一假设使得朴素贝叶斯的学习成为可能。朴素贝叶斯算法具体步骤如下。

首先计算类先验概率：

类先验概率可直接用极大似然估计进行计算。

然后计算类条件概率：

最后给定新的实例，计算其对应的最大后验概率，然后判断其所属的类别：

     以上就是朴素贝叶斯的基本原理。下面基于numpy和pandas来实现朴素贝叶斯算法。

导入package：

import numpy as np
import pandas as pd

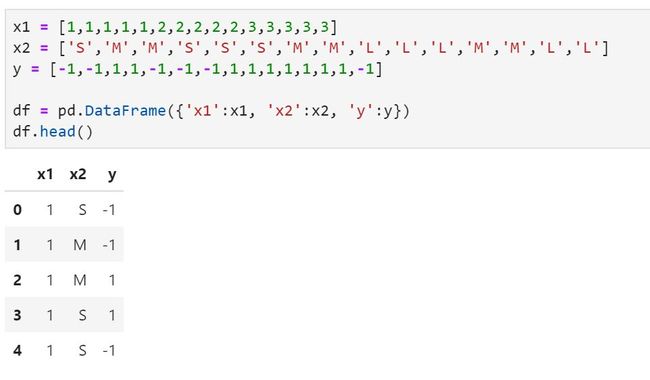
创建示例数据集：

x1 = [1,1,1,1,1,2,2,2,2,2,3,3,3,3,3]
x2 = ['S','M','M','S','S','S','M','M','L','L','L','M','M','L','L']
y = [-1,-1,1,1,-1,-1,-1,1,1,1,1,1,1,1,-1]


df = pd.DataFrame({'x1':x1, 'x2':x2, 'y':y})
df.head()

取出特征和标签：

X = df[['x1', 'x2']]
y = df[['y']]

定义朴素贝叶斯训练过程：

def nb_fit(X, y):
    classes = y[y.columns[0]].unique()
    class_count = y[y.columns[0]].value_counts()
    class_prior = class_count/len(y)
    
    prior = dict()
    for col in X.columns:
        for j in classes:
            p_x_y = X[(y==j).values][col].value_counts()
            for i in p_x_y.index:
                prior[(col, i, j)] = p_x_y[i]/class_count[j]
    return classes, class_prior, prior

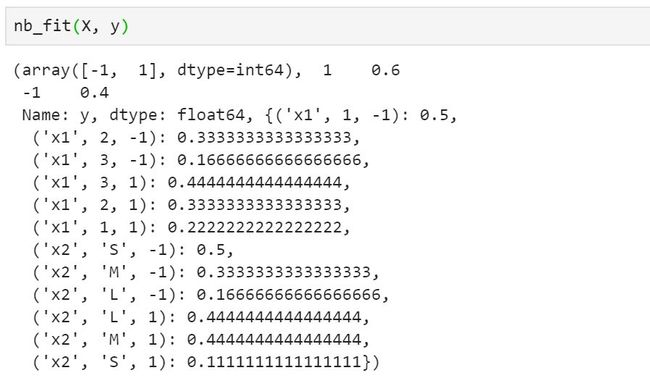
拟合示例如下：

最后定义预测函数：

def predict(X_test):
    res = []
    for c in classes:
        p_y = class_prior[c]
        p_x_y = 1
        for i in X_test.items():
            p_x_y *= prior[tuple(list(i)+[c])]
        res.append(p_y*p_x_y)
    return classes[np.argmax(res)]

给定测试实例并进行预测：

X_test = {'x1': 2, 'x2': 'S'}
classes, class_prior, prior = nb_fit(X, y)
print('测试数据预测类别为：', predict(X_test))

最后也可以定义一个Naive_Bayes的类对上述过程进行封装：

import numpy as  np
import pandas as pd


class Naive_Bayes:
    def __init__(self):
        pass


    # 朴素贝叶斯训练过程
    def nb_fit(self, X, y):
        classes = y[y.columns[0]].unique()
        class_count = y[y.columns[0]].value_counts()
        # 类先验概率
        class_prior = class_count / len(y)
        # 计算类条件概率
        prior = dict()
        for col in X.columns:
            for j in classes:
                p_x_y = X[(y == j).values][col].value_counts()
                for i in p_x_y.index:
                    prior[(col, i, j)] = p_x_y[i] / class_count[j]


        return classes, class_prior, prior


    # 预测新的实例
    def predict(self, X_test):
        res = []
        for c in classes:
            p_y = class_prior[c]
            p_x_y = 1
            for i in X_test.items():
                p_x_y *= prior[tuple(list(i) + [c])]
            res.append(p_y * p_x_y)
        return classes[np.argmax(res)]




if __name__ == "__main__":
    x1 = [1, 1, 1, 1, 1, 2, 2, 2, 2, 2, 3, 3, 3, 3, 3]
    x2 = ['S', 'M', 'M', 'S', 'S', 'S', 'M', 'M', 'L', 'L', 'L', 'M', 'M', 'L', 'L']
    y = [-1, -1, 1, 1, -1, -1, -1, 1, 1, 1, 1, 1, 1, 1, -1]
    df = pd.DataFrame({'x1': x1, 'x2': x2, 'y': y})
    X = df[['x1', 'x2']]
    y = df[['y']]
    X_test = {'x1': 2, 'x2': 'S'}


    nb = Naive_Bayes()
    classes, class_prior, prior = nb.nb_fit(X, y)
    print('测试数据预测类别为：', nb.predict(X_test))

     以上就是本节内容，下一讲我们来看看贝叶斯分类的另一种形态——贝叶斯网络。完整代码文件和数据可参考笔者GitHub地址：

https://github.com/luwill/machine-learning-code-writing

参考资料：

https://github.com/SmirkCao/Lihang

李航 统计学习方法

往期精彩：

数学推导+纯Python实现机器学习算法10：线性不可分支持向量机

数学推导+纯Python实现机器学习算法8-9：线性可分支持向量机和线性支持向量机

数学推导+纯Python实现机器学习算法6：感知机

数学推导+纯Python实现机器学习算法5：决策树之CART算法

数学推导+纯Python实现机器学习算法4：决策树之ID3算法

数学推导+纯Python实现机器学习算法3：k近邻

数学推导+纯Python实现机器学习算法2：逻辑回归

数学推导+纯Python实现机器学习算法1：线性回归

往期精彩回顾




适合初学者入门人工智能的路线及资料下载机器学习及深度学习笔记等资料打印机器学习在线手册深度学习笔记专辑《统计学习方法》的代码复现专辑
AI基础下载机器学习的数学基础专辑获取一折本站知识星球优惠券，复制链接直接打开：https://t.zsxq.com/yFQV7am本站qq群1003271085。加入微信群请扫码进群：