FP-growth算法高效实现

摘要：

  搜索引擎中，输入一个单词或者单词的一部分。搜索引擎就会自动补全查询的单词项。用户甚至实现都不知道搜索引擎推荐的东西是否存在。搜索引擎公司研究元需要查看互联网上的词找出经常出线一起的词对。

它是基于Apriori算法，但是比它快。这里的任务是将数据集存储在一个特定的FP树结构中发现频繁项集或者频繁项对。

过程简化如下：会两次扫描数据集

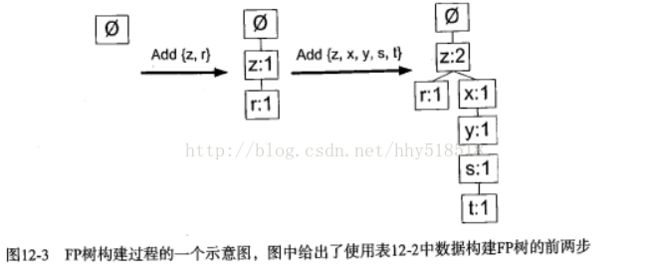
1）构建FP树

2）从FP树中挖掘频繁项集

下面的例子是：基于Twiter文本流中挖掘常用词

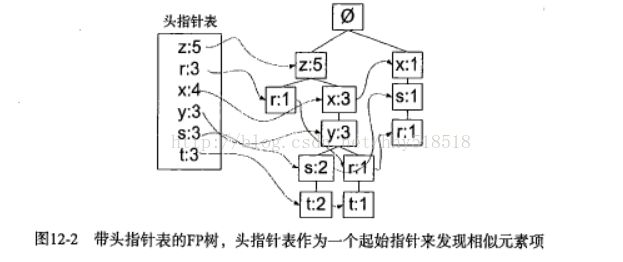
FP-growth算法就是将数据存储在一个称作FP树的紧凑的数据结构中。FP代表的是频繁模式。它通过link来链接相似的元素，被连起来的元素看作一个链表。同搜索树不同的是，一个元素项可以在FP树中出现很多次。FP树会存储项集的出线频率，而每个项集会以路径方式存储在树中。树节点上给出集合中单个元素以及序列的出线次数，路径会给出这个序列的出线次数。

相似项链接就是节点链接，用于快速发现相似项的位置。我们生成上图树的事务数据

FP-growth算法工作流程如下：首先构建FP树，对原始数据集合扫描两次。第一次所有元素出现次数进行计数，如果某个元素不频繁那么超集肯定不频繁。

第二遍只考虑那些频繁元素

FP树的数据结构

class treeNode:
    def __init__(self,nameValue,numOccur,parentNode):
        self.name = nameValue
        self.parent = parentNode
        self.count = numOccur
        self.nodeLink = None
        self.children={}
    def inc(self,numOccur):
        self.count+=numOccur
    #树文本形式打印
    def disp(self,ind=1):
        print ' '*ind,self.name, ' ',self.count
        for child in self.children.values():
            child.disp(ind+1)
    

我们测试一下这个数据结构

import fpGrowth

rootNode = fpGrowth.treeNode('pyramid',9,None)
rootNode.children['eye'] = fpGrowth.treeNode('eye',13,None)

rootNode.disp()

可以看到打印出来的结果如下：

  pyramid   9
   eye   13

构建FP树

这里使用字典数据结构保存头指针列表。除了存放指针以外。头指针还用来保存FP树每类元素的总数。第一次遍历数据集的时候获得每个元素的出现频率。接下来过滤掉不满足最小支持度的元素项目。对于每个事务集去掉不满足支持度的元素，然后按照出现频率进行每个元素排序。排序后基于元素项的绝对出现频率进行。

过滤排序以后就是构建树了。从空集开始想其中不断添加频繁项集。如果树中已经有元素，则增加现有的元素值。如果不存在添加分支

代码实现如下：

#dataset存储的trans的出现频率
def createTree(dataSet,minSup=1):
    headTable = {}
    for trans in dataSet:
        for item in trans:
            headTable[item] = headTable.get(item,0) + dataSet[trans]
    for k in headTable.keys():
        if headTable[k]0:
            orderedItems = [v[0] for v in sorted(localD.items(),key=lambda p:p[1],reversed=True)]#变成元祖数组
            updateTree(orderedItems,retTree,headTable,count)
    return retTree,headTable

def updateTree(items,inTree,headTable,count):
    if items[0] in inTree.children:
        inTree.children[items[0]].inc(count)
    else:
        inTree.children[items[0]] = treeNode(items[0],count,inTree)
        if headTable[items[0]][1] == None:#没有链接节点
            headTable[items[0]][1] = inTree.children[items[0]]#存放头节点
        else:#更新表的头指针
            updateHeader(headTable[items[0]][1],inTree.children[items[0]])
    if len(items)>1:#更新其他孩子节点
        updateTree(items[1::],inTree.children[items[0]],headTable,count)
#在链表末尾添加
def updateHeader(nodeToTest,targetNode):
    while(nodeToTest.nodeLink!=None):
        nodeToTest = nodeToTest.nodeLink
    nodeToTest.nodeLink = targetNode

我们生成我们的随机数据集，然后每个事务用字典形式存储为数据集

def loadSimpDat():
    simpDat=[['r','z','h','j','p'],
             ['z','y','x','w','v','u','t','s'],
             ['z'],
             ['r','x','n','o','s'],
             ['y','r','x','z','q','t','p'],
             ['y','z','x','e','q','s','t','m']]
    return simpDat

#创建成为frozenset
def createInitSet(dataSet):
    retDict={}
    for trans in dataSet:
        retDict[frozenset(trans)] = 1#出现次数
    return retDict

测试如下：

simpDat = fpGrowth.loadSimpDat()
simpDat

initSet = fpGrowth.createInitSet(simpDat)
initSet

mpFPtree,myHeaderTab = fpGrowth.createTree(initSet,3)

mpFPtree.disp()

  Null Set   1
   x   1
    s   1
     r   1
   z   5
    x   3
     y   3
      s   2
       t   2
      r   1
       t   1
    r   1
当我们构建成功这棵树以后就可以进行频繁模式的挖掘了。

频繁模式挖掘

从FP树抽取频繁项集的基本步骤如下：

从FP树获得条件模式基

利用条件模式基，构建一个条件FP树

重复步骤直到只包含一个元素

抽取条件模式基

对于每一个元素项，获得对应的条件模式基。条件模式基是查找元素项位结尾的路径集合。每一条路径其实前缀路径。一条前缀路径是介于查找元素项和根节点之间内容

为了获得前缀路径，可以用树进行穷举搜索。可以利用前面创建的头指针获得更有效的方法。头指针包含链表的起始指针。一旦到达每个元素就可以回溯到根节点。

def ascendTree(leafNode,prefixPath):
    if leafNode.parent!=None:
        prefixPath.append(leafNode.name)
        ascendTree(leafNode.parent,prefixPath)


def findPrefixPath(basePat,treeNode):
    condPats={}
    while treeNode!=None:
        prefixPath={}
        ascendTree(treeNode,prefixPath)
        if len(prefixPath)>1:
            condPats[frozenset(prefixPath[1:])] = treeNode.count
        treeNode = treeNode.nodeLink
    return condPats

访问树中所有包含给定元素项的节点来完成。创建树的时候头指针指向了第一个元素项。该元素项也会链接到后续的元素项。

print fpGrowth.findPrefixPath('x',myHeaderTab['x'][1])

{frozenset(['z']): 3}

print fpGrowth.findPrefixPath('r',myHeaderTab['r'][1])

{frozenset(['x', 's']): 1, frozenset(['z']): 1, frozenset(['y', 'x', 'z']): 1}

创建条件FP树

对于每一个频繁项，我们都要创建一个条件FP树。

根据这个图。比如我们探索的是y那么条件基就是{(z,x),3}那么我们递归处理前缀{z},{z,x},{x}等若他们和{y}组成的项集都是满足最小支持度的那么就是频繁项集

#递归查找频繁项集
def minTree(inTree,headerTable,minSup,preFix,freqItemList):
    #从小到大排序
    bigL = [v[0] for v in sorted(headerTable.items(),
                                 key=lambda p:p[1])]
    #从下往上找
    for basePat in bigL:
        newFreqSet = preFix.copy()
        newFreqSet.add(basePat)
        freqItemList.append(newFreqSet)
        condPattBases = findPrefixPath(basePat,headerTable[basePat][1])
        myCondTree,myHead = createTree(condPattBases,minSup)
        #树中有元素的话
        if myHead!=None:
            minTree(myCondTree,myHead,minSup,newFreqSet,freqItemList)

就是一个从下往上查找的过程。

因为头指针指向的一个元素可能是几个分支上的总数。所以每个分支可能都不是频繁项集。因为若子集是频繁项集。那么超集就有可能是频繁项集这个定理来看

freqItems = []
fpGrowth.minTree(mpFPtree,myHeaderTab,3,set([]),freqItems)

print freqItems

得到如下的结果

[set(['y']), set(['y', 'x']), set(['y', 'z']), set(['y', 'x', 'z']), set(['s']), set(['x', 's']), set(['t']), set(['y', 't']), set(['x', 't']), set(['y', 'x', 't']), set(['z', 't']), set(['y', 'z', 't']), set(['x', 'z', 't']), set(['y', 'x', 'z', 't']), set(['r']), set(['x']), set(['x', 'z']), set(['z'])]