基于python的数据结构和算法（北京大学）第七章（排序和查找）

• 顺序查找Sequential Search：
  无序表顺序查找:

def sequentialSearch(alist,item):
    pos = 0
    found = False
    
    while pos

有序表顺序查找：

def orderedSequentialSearch(alist,item):
    pos = 0
    found = False
    stop = False
    while pos item:
                stop = True
            else:
                pos += 1
    return found

关键在于有序时，加入stop参数来控制循环，当出现第一个比所查找目标大的数时，即不必查找后面的数，可直接进入下一轮循环，这样可以有效降低查找的时间复杂度。

• 二分查找：
  二分查找主要应用于有序表，每次都查找当前部分有序表的中间值进行比较。由于为有序表，比较非相等之后，便可根据比较的大小，进入左侧或右侧的部分有序表进行再次取中间值对比。

非递归实现：

def binarySearch(alist,item):
    first = 0
    last = len(alist)-1
    found = False

    while first<=last and not found:
        midpoint = (first+last)/2
        if alist[midpoint]==item:
            found = True
        else:
            if item

递归实现：

def binarySearch(alist,item):
    if len(alist) == 0:
        return False
    else:
        midpoint = len(alist)/2
        if alist[midpoint] == item:
            return True
        else:
            if item

• 冒泡排序：
  冒泡排序算法的思路在于对无序表进行多趟比较交换。每趟包括了多次两两相邻比较，并将逆序的数据项交换位置，最终能将本趟的最大项就位。经过n-1趟比较，实现整表排序。每趟的过程类似“气泡”在水上不断上浮到水面的过程。

def bubbleSort(alist):
    for passnum in range(len(alist)-1,0,-1):
        for i in range(passnum):
            if alist[i]>alist[i+1]:
                temp = alist[i]
                alist[i] = alist[i+1]
                alist[i+1] = temp  # <=> alist[i],alist[i+1] = alist[i+1],alist[i]

对于冒泡排序，冒泡排序时间效率较差，复杂度为O(n^2)。但无需任何额外的存储空间开销。
算法过程总需要n-1趟，随着趟数的增加，比对的次数逐步从n-1减少到1，并包括可能发生的数据项交换。因此，比对的次数为1 – n-1 的累加，为1/2n^2 - 1/2n。
最好的情况为列表在排序前已经有序，交换次数为0，最差的情况是每次比对都要进行交换，交换次数等于比对次数。平均情况为最差情况的一半。
冒泡排序通常作为时间效率较差的排序算法，来作为其他算法的对比基准。

 - 对冒泡排序算法的改进，可以通过监测每趟比对是否发生过交换，可以提前确定排序是否完成。如果某趟比对没有发生任何交换，说明列表已经排好序，可以提前结束算法。

def shortBubbleSort(alist):
    exchange = True
    passnum = len(alist)-1
    while passnum > 0 and exchange:
        exchange = False
        for i in range(passnum):
            if alist[i]>alist[i+1]:
                exchange = True
                alist[i],alist[i+1] = alist[i+1],alist[i]

        passnum = passnum-1

• 选择排序（Selection Sort）
  选择排序对冒泡排序进行了改进，保留了其基本的多趟比对思路，每趟都使当前最大项就位。但是选择排序对交换进行了削减，相比起冒泡排序进行多次交换，每趟仅进行一次交换，记录最大项所在位置，最后再跟本趟最后一项交换。在时间复杂度上，比冒泡稍优。对比次数不变，O（n^2)。而交换次数则减少为了O（n）。
  重复（元素个数-1）次
  选择排序的过程为：
  把第一个没有排序过的元素设置为最小值
  遍历每个没有排序过的元素
  如果元素 < 现在的最小值
  将此元素设置成为新的最小值
  将最小值和第一个没有排序过的位置交换

def selectionsort(alist):
    for i in range(len(alist)):
        minindex = i
        for j in range(i,(len(alist))):
            if alist[j] < alist[minindex]:
                minindex = j
        temp = alist[i]
        alist[i] = alist[minindex]
        alist[minindex] = temp

    return alist

print(selectionsort([1,5,7,3,7,0,2,8,3,99,44,35]))

标准代码

def selectionSort(alist):
    for fillslot in range(len(alist)-1,0,-1):
        positionOFMAX = 0
        for location in range(1,fillslot+1):
            if alist[location]>alist[positionOFMAX]:
                positionOFMAX = location

        temp = alist[fillslot]
        alist[fillslot] = alist[positionOFMAX]
        alist[positionOFMAX] = temp

• 插入排序（Insertion Sort）
  插入排序时间复杂度仍然是O（n^2)，但思路有所变化。
  插入排序维持一个已排好序的子列表，其位置始终在列表的前部，然后逐步扩大这个子列表直到全表。
  算法过程：
  将第一个元素标记为已排序

遍历每个没有排序过的元素

“提取” 元素 X

i = 最后排序过元素的指数 到 0 的遍历

如果现在排序过的元素 > 提取的元素

  将排序过的元素向右移一格

否则：插入提取的元素

def insertionSort(alist):
    for index in range(1,len(alist)):

        currentvalue = alist[index]
        position = index

        while position>0 and alist[position-1]>currentvalue:
            alist[positon]=alist[position-1]
            position -= 1

        alist[position] = currentvalue

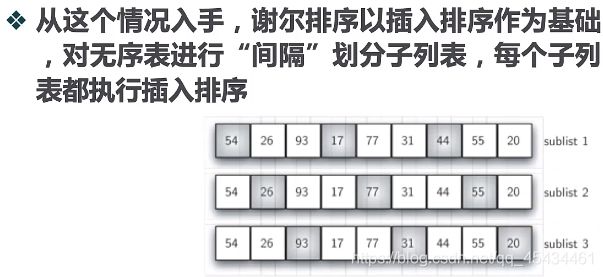
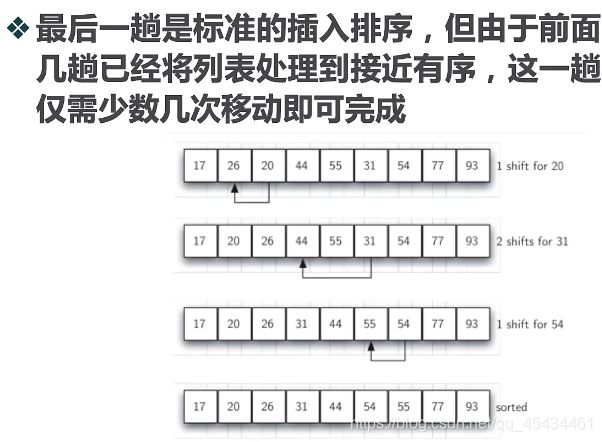
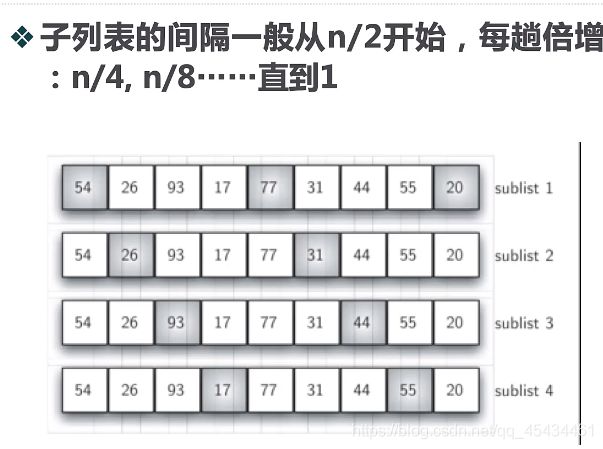
• 谢尔排序（Shell Sort）

我们注意到插入排序的比对次数，在最好的情况下是O（n），这种情况发生在列表已是有序的情况下，实际上。列表越接近有序，插入排序的比对次数就越少。
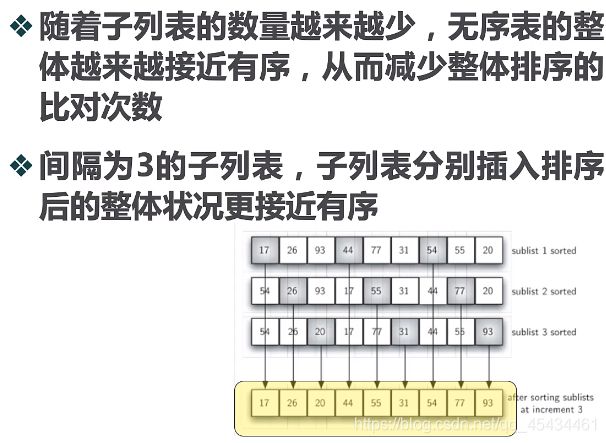
从这个情况入手，谢尔排序，以插入排序作为基础，对无序表进行”间隔“划分子列表，每个子列表都执行插入排序。

def shellSort(alist):
    sublistcount = len(alist)//2  # 返回整数值
    while sublistcount>0:
        for startposition in range(sublistcount):
            gapInsertionSort(alist,startPosition,sublistcount)
        print("after increments of size",sublistcount,
              "the list is ",alist)
        sublistcount = sublistcount//2

def gapInsertionSort(alist,start,gap):
    for i in range(start+gap,len(alist),gap):
        currentvalue = alist[i]
        position = i
        while position>=gap and alist[position-gap]>currentvalue:
            alist[positon] = alist[position-gap]
            position -= gap

        alist[position] = currentvalue

• 归并排序（Merge Sort）
  
  

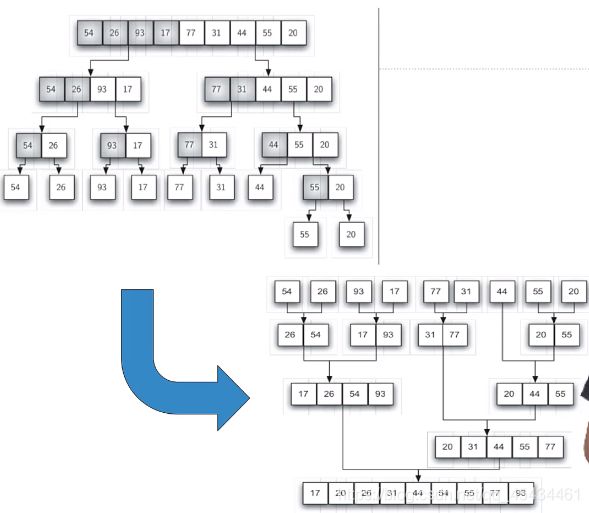
def mergeSort(alist):
    if len(alist)>1:
        mid = len(alist)//2
        lefthalf = alist[:mid]
        righthalf = alist[mid:]

        mergeSort(lefthalf)
        mergeSort(righthalf)

        i = j = k = 0
        while i< len(lefthalf) and j

更具有python风格的代码：

def merge_sort(lst):
    if len(lst)<=1:
        return lst
    
    middle = len(lst)//2
    left = merge_sort(lst[:middle])
    right = merge_sort(lst[middle:])
    
    merged = []
    while left and right:
        if left[0] <= right[0]:
            merged.append(left.pop(0))
        else:
            merged.append(right.pop(0))
    merged.extend(right if right else left)
    return merged

• 快速排序（Quick Sort）
  
  
  
  依据一个中值数据项将数据表分为两半，每部分分别进行快速排序（递归）

def quickSort(alit):
    quickSortHelper(alist,0,len(alist)-1)

def quickSortHelper(alist,first,last):
    if first=pivotvalue and \
            rightmark>=leftmark:
            rightmark -=1
        if rightmark