Arima预测模型(R语言)
ARIMA(p,d,q)
模型全称为
差分自回归移动平均模型(Autoregressive Integrated Moving Average Model,简记ARIMA),
AR是自回归, p为自回归项; MA为移动平均,q为移动平均项数,d为时间序列成为平稳时所做的差分次数。
所谓ARIMA模型,是指将非平稳时间序列转化为平稳时间序列,然后将因变量仅对它的滞后值以及随机误差项的现值和滞后值进行回归所建立的模型。ARIMA模型根据原序列是否平稳以及回归中所含部分的不同,包括移动平均过程(MA)、自回归过程(AR)、自回归移动平均过程(ARMA)以及ARIMA过程。
下面我们选取了一些具有周期性(7天)的测试数据,通过ARIMA模型做一个简单的预测。
source<- c(10930,10318,10595,10972,7706,6756,9092,10551,9722,10913,11151,8186,6422,
6337,11649,11652,10310,12043,7937,6476,9662,9570,9981,9331,9449,6773,6304,9355,10477,
10148,10395,11261,8713,7299,10424,10795,11069,11602,11427,9095,7707,10767,12136,12812,
12006,12528,10329,7818,11719,11683,12603,11495,13670,11337,10232,13261,13230,15535,
16837,19598,14823,11622,19391,18177,19994,14723,15694,13248,9543,12872,13101,15053,
12619,13749,10228,9725,14729,12518,14564,15085,14722,11999,9390,13481,14795,15845,
15271,14686,11054,10395,14775,14618,16029,15231,14246,12095,10473,15323,15381,14947)
测试数据的时间序列图,如下:
data<-xts(data,seq(as.POSIXct("2014-01-01"),len=length(data),by="day"))
plot(data)

通过以下代码:
data_diff1<-diff(data,differences=1)
plot(data_diff1)
data_diff2<-diff(data,differences=2)
plot(data_diff2)
可以看出一次差分后的时间序列在均值和方差上看起来像是平稳的,与二次差分的图形相差不大,随着时间推移,时间序列大致保持不变,因此设置差分项d=1。
接下来需要选择合适的ARIMA模型,即确定ARIMA(p,d,q)中合适的 p、q 值,我们通过R中的“acf()”和“pacf”函数来做判断。
1、查看自相关图
acf <- acf(data_diff1,lag.max=100,plot=FALSE)
plot(acf)

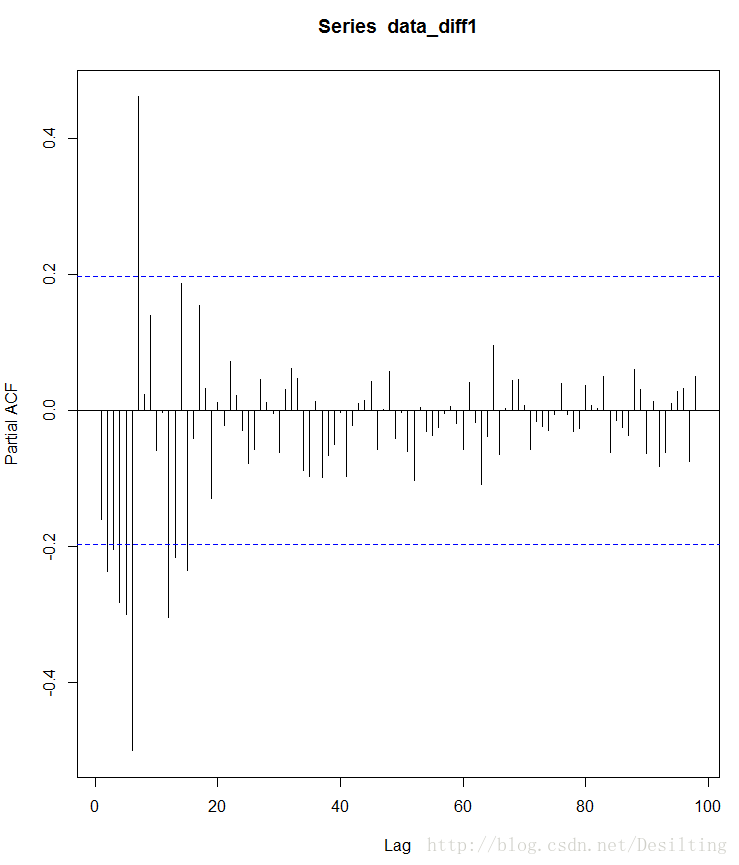
2、查看偏自相关图
pacf <- pacf(data_diff1,lag.max=100,plot=FALSE)
plot(pacf)
| 模型 |
ACF |
PACF |
| AR(p) |
衰减趋于零(几何型或振荡型) |
p阶后截尾 |
| MA(q) |
q阶后截尾 |
衰减趋于零(几何型或振荡型) |
| ARMA(p,q) |
q阶后衰减趋于零(几何型或振荡型) |
p阶后衰减趋于零(几何型或振荡型) |
因此我们的arima模型为arima(7,1,0)
data.fit <- arima(data,order=c(7,1,0), seasonal=list(order=c(1,1,0), period=7))
data.fit
|
Series: data
ARIMA(7,1,0)(1,1,0)[7]
Coefficients:
ar1 ar2 ar3 ar4 ar5 ar6 ar7 sar1
-0.2829 -0.2128 -0.0180 0.0606 0.3164 0.0415 -0.0883 -0.5075
s.e. 0.1040 0.1076 0.1076 0.1048 0.1062 0.1066 0.1520 0.1449
sigma^2 estimated as 1589493: log likelihood=-789.34
AIC=1596.68 AICc=1598.88 BIC=1619.38
|
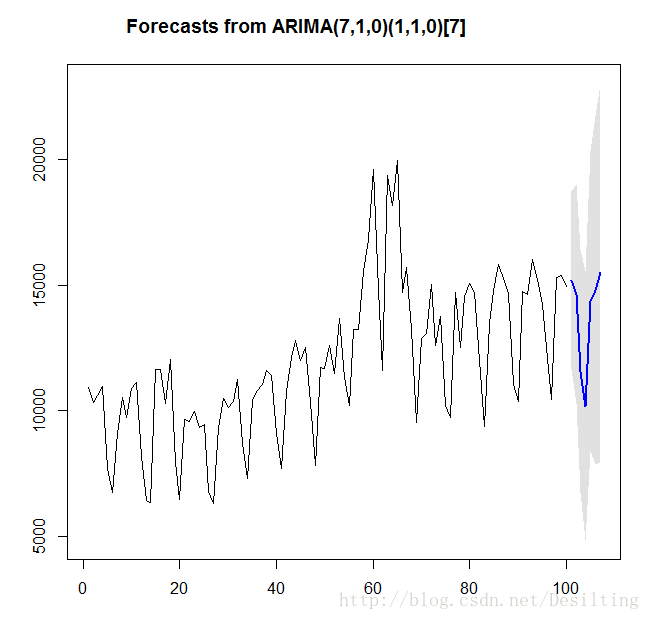
预测后一周的值:
forecast <- forecast.Arima(data.fit,h=7,level=c(99.5))
forecast
plot.forecast(forecast)
|
Forecast Lo 80 Hi 80 Lo 95 Hi 95
101 15206.61 13590.892 16822.33 12735.583 17677.64
102 14654.18 12665.935 16642.42 11613.422 17694.94
103 11589.60 9388.579 13790.62 8223.428 14955.77
104 10190.69 7742.040 12639.34 6445.803 13935.58
105 14362.50 11640.733 17084.26 10199.919 18525.07
106 14785.77 11620.577 17950.96 9945.025 19626.52
107 15501.02 12049.124 18952.91 10221.802 20780.23
|
tsdiag检验——
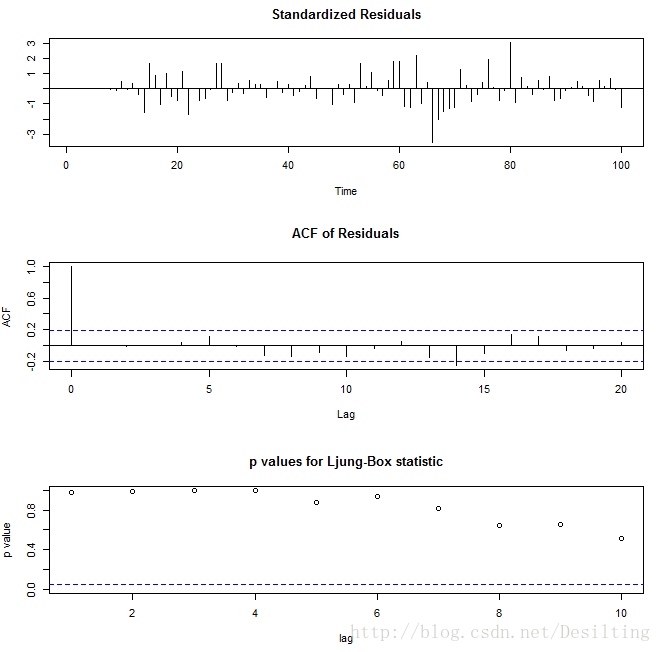
Acf检验说明:
残差没有明显的自相关性
Ljung-Box测试显示:
所有的P-value>0.5, 说明残差为白噪声
*最近正在看这一块的东西,有些地方还没弄太明白,尤其是公式原理,若有不正确的地方,欢迎指正。
如何用R做单变量的时间序列?
---加载时间序列程序包
library(tseries)
--使用该包自带的程序,是指航空乘客的分布
air <- AirPassengers
--作这个时间序列的图,通过图作一个直观判断
ts.plot(air)
--查看自相关图
acf(air)
--查看偏相关图
pacf(air)
--初步判断
--1、有趁势。2、可能有季节性。3、应该使用MA()模型来拟合
--通过decompose 进行分解:随机、趋势、季节
x<-decompose(air)
---作图查看
plot(x)
plot(x$seasonal)
---选择合适的模型拟合
---趋势通过差分来消除
---季节性因素,确定相应的period
air.fit <- arima(air,order=c(0,1,1), seasonal=list(order=c(0,1,1), period=12))
---对结果进行诊断
tsdiag(air.fit)
--加载时间序列包
library(forecast)
--向前预测12期,默认情况下24期
--给出80%,95%置信度下的置信区间
air.forecast <- forecast(air.fit,12)
plot.forecast(air.forecast)
这里只是简单用到R自带的数据做了一个简单的演示过程,找个时间我再完整写一篇关于时间序列建模过程的文章,以及如何判断时间序列的P、Q、I等参数的确定。
|
|