ID3具有一定的局限性,即信息增益倾向于选择取值比较多的特征(特征越多,条件熵(特征划分后的类别变量的熵)越小,信息增量就越大),C4.5通过选择最大的信息增益率 gain ratio 来选择节点可以解决该问题。并且C4.5算法可以处理连续和有缺失值的数据。
C4.5与ID3在实现过程中,不同之处在于将计算信息增益的函数改为计算信息增益率。
譬如,对于上一个例子中的湿度这一项的取值改为:
| Day |
Outlook |
Temperature |
Humidity |
Wind |
PlayTennis |
| 1 |
Sunny |
Hot |
85 |
Weak |
No |
| 2 |
Sunny |
Hot |
90 |
Strong |
No |
| 3 |
Overcast |
Hot |
78 |
Weak |
Yes |
| 4 |
Rain |
Mild |
96 |
Weak |
Yes |
| 5 |
Rain |
Cool |
80 |
Weak |
Yes |
| 6 |
Rain |
Cool |
70 |
Strong |
No |
| 7 |
Overcast |
Cool |
65 |
Strong |
Yes |
| 8 |
Sunny |
Mild |
95 |
Weak |
No |
| 9 |
Sunny |
Cool |
70 |
Weak |
Yes |
| 10 |
Rain |
Mild |
80 |
Weak |
Yes |
| 11 |
Sunny |
Mild |
70 |
Strong |
Yes |
| 12 |
Overcast |
Mild |
90 |
Strong |
Yes |
| 13 |
Overcast |
Hot |
75 |
Weak |
Yes |
| 14 |
Rain |
Mild |
80 |
Strong |
No |
Gain(Wind) = Entropy(S) – (8/14)* Entrogy(weak)-(6/14)* Entrogy(strong) = 0.048
weak = 8;Strong = 6
Feature(Wind) = -8/14*log(8/14)-6/14*log(6/14) = 0.9852
RatioGain(Wind) = Gain(Wind)/Feature (Wind) = 0.0487
同理:RatioGain(Outlook) = 0.247/1.577 = 0.1566
RatioGain(Temperature)= 0.029/1.556 = 0.018
其中,对于连续值的计算:
1. 对特征的取值进行升序排序
2. 两个特征取值之间的中点作为可能的分裂点,将数据集分成两部分,计算每个可能的分裂点的信息增益(InforGain)。优化算法就是只计算分类属性发生改变的那些特征取值。
3. 选择修正后信息增益(InforGain)最大的分裂点作为该特征的最佳分裂点
4. 计算最佳分裂点的信息增益率(Gain Ratio)作为特征的Gain Ratio。注意,此处需对最佳分裂点的信息增益进行修正:减去log2(N-1)/|D|(N是连续特征的取值个数,D是训练数据数目,此修正的原因在于:当离散属性和连续属性并存时,C4.5算法倾向于选择连续特征做最佳树分裂点)
故,划分为:{ 65、70、75、78、80、85、90、95、96 } 这几个特征。
|
|
65 |
70 |
75 |
78 |
80 |
85 |
90 |
95 |
96 |
|||||||||
|
|
≤ |
> |
≤ |
> |
≤ |
> |
≤ |
> |
≤ |
> |
≤ |
> |
≤ |
> |
≤ |
> |
≤ |
> |
| Yes |
1 |
8 |
3 |
6 |
4 |
5 |
5 |
4 |
7 |
2 |
7 |
2 |
8 |
1 |
8 |
1 |
9 |
0 |
| No |
0 |
5 |
1 |
4 |
1 |
4 |
1 |
4 |
2 |
3 |
3 |
2 |
4 |
1 |
5 |
0 |
5 |
0 |
| Entropy |
0 |
0.961 |
0.811 |
0.971 |
0.722 |
0.991 |
0.65 |
1 |
0.764 |
0.971 |
0.881 |
1 |
0.918 |
1 |
0.961 |
0 |
0.94 |
0 |
| Gain |
0.048 |
0.015 |
0.045 |
0.090 |
0.102 |
0.025 |
0.011 |
0.048 |
0 |
|||||||||
此时,可以看到当特征小于等于80时,信息增益最大,选取该取值区间作为湿度属性的信息增益。
即Gain(Humidity) = 0.102
Feature(Humidity) = -9/14*log(9/14) - 5/14*log(5/14) = 0.940(两个分支,大于80的和小于等于80的)
RatioGain(Humidity) = 0.102/0.940 = 1.085
//------------------------------------------------
对于ID3算法局限性的理解:
X = [['sunny', 'hot', 'h_85', 'weak'],
['sunny', 'hot', 'h_90', 'strong'],
['overcast', 'hot', 'h_78', 'weak'],
['rain', 'mild', 'h_96', 'weak'],
['rain', 'cool', 'h_80', 'weak'],
['rain', 'cool', 'h_70', 'strong'],
['overcast', 'cool', 'h_65', 'strong'],
['sunny', 'mild', 'h_95', 'weak'],
['sunny', 'cool', 'h_70', 'weak'],
['rain', 'mild', 'h_80', 'weak'],
['sunny', 'mild', 'h_70', 'strong'],
['overcast', 'mild', 'h_90', 'strong'],
['overcast', 'hot', 'h_75', 'weak'],
['rain', 'mild', 'h_80', 'strong'],
]
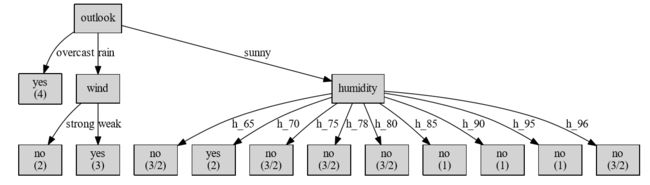
对于ID3算法的输入改为,可以看到生成的决策树为:
可以看到,此时就会出现过拟合的现象。
而采用信息增益率作为判决条件的话:
estimator = Id3Estimator(gain_ratio=1)
获得的决策树为:
因此,对于使用信息增益作为分类准则和使用信息增益率的区别如上所示。
//-----------------------------------
对于处理数值的理解:
解读python的第三方库,ID3模块(decision-tree-id3)
在其中id3.py模块中:
Id3Estimator类的fit函数中
for i in range(self.n_features):
if check_input and check_numerical_array(X_[:, i]):
self.is_numerical[i] = True
X_tmp[:, i] = X_[:, i]
else:
X_tmp[:, i] = self.X_encoders[i].fit_transform(X_[:, i])
这里会判断一下传递的特征是名字还是数字,判断的方法在checks.py中:
def check_numerical_array(array):
""" Check if all values in a 1d array are numerical. Raises error if array
is more than 1d.
Parameters
----------
array : nparray
containing the class names
Returns
-------
result : bool
True if all values in array are numerical, otherwise false
"""
try:
if array.ndim > 1:
raise ArithmeticError("Found array with dim {}. Expected = 1."
.format(array.ndim))
array.astype(np.float64)
return True
except ValueError:
return False
此处会做一个类型转换,如果输入的是数字、字符串形式的数字都会被转为float类型。
(此次我觉得不太妥当,字符串形式的数字不应该转化为数字,说不定人家就是想这样输入作为feature呢,譬如我上面的输入数字的开头还要加一个 ‘h_’)
当特征为数字的时候计算方法在splitter.py文件中:
def _info_numerical(self, x, y):
""" Info for numerical feature feature_values
sort values then find the best split value
Parameters
----------
x : np.array of shape [n remaining examples]
containing feature values
y : np.array of shape [n remaining examples]
containing relevent class
Returns
-------
: float
information for remaining examples given feature
: float
pivot used set1 < pivot <= set2
"""
n = x.size
sorted_idx = np.argsort(x, kind='quicksort')
sorted_y = np.take(y, sorted_idx, axis=0)
sorted_x = np.take(x, sorted_idx, axis=0)
min_info = float('inf')
min_info_pivot = 0
min_attribute_counts = np.empty(2)
for i in range(1, n):
if sorted_x[i - 1] != sorted_x[i]:
tmp_info = i * self._entropy(sorted_y[0: i]) + \
(n - i) * self._entropy(sorted_y[i:])
if tmp_info < min_info:
min_attribute_counts[SplitRecord.LESS] = i
min_attribute_counts[SplitRecord.GREATER] = n - i
min_info = tmp_info
min_info_pivot = (sorted_x[i - 1] + sorted_x[i]) / 2.0
return CalcRecord(CalcRecord.NUM,
min_info * np.true_divide(1, n),
pivot=min_info_pivot,
attribute_counts=min_attribute_counts)
可以看到,其计算过程和上述对于数值的计算过程一样,其min_info为选取的最小的分类后的信息熵,为了得到最大的信息增益。
而对于是否使用信息增益率的判断在splitter.py文件中:
def _is_better(self, calc_record1, calc_record2):
"""Compares CalcRecords using gain ratio if present otherwise
using the information.
Parameters
----------
calc_record1 : CalcRecord
calc_record2 : CalcRecord
Returns
-------
: bool
if calc_record1 < calc_record2
"""
if calc_record1 is None:
return True
if calc_record2 is None:
return False
if self.gain_ratio:
if calc_record1.gain_ratio is None:
calc_record1.gain_ratio = self._gain_ratio(calc_record1)
if calc_record2.gain_ratio is None:
calc_record2.gain_ratio = self._gain_ratio(calc_record2)
if self._is_close(calc_record1.gain_ratio,
calc_record2.gain_ratio):
return calc_record1.info > calc_record2.info
else:
return calc_record1.gain_ratio < calc_record2.gain_ratio
else:
return calc_record1.info > calc_record2.info
故,对于C4.5算法,同样可以使用ID3模块,只不过设置参数:gain_ratio=True即可。
得到的决策树为:
下面我们验证在sunny情况下,humidity的划分便准是否正确:
| Day |
Outlook |
Temperature |
Humidity |
Wind |
PlayTennis |
| 1 |
Sunny |
Hot |
85 |
Weak |
No |
| 2 |
Sunny |
Hot |
90 |
Strong |
No |
| 8 |
Sunny |
Mild |
95 |
Weak |
No |
| 9 |
Sunny |
Cool |
70 |
Weak |
Yes |
| 11 |
Sunny |
Mild |
70 |
Strong |
Yes |
首先计算humidity:
|
|
70 |
85 |
90 |
95 |
||||
|
|
≤ |
> |
≤ |
> |
≤ |
> |
≤ |
> |
| Yes |
2 |
0 |
2 |
0 |
2 |
0 |
2 |
0 |
| No |
0 |
3 |
1 |
2 |
2 |
1 |
3 |
0 |
| Entropy |
0 |
0 |
0.756 |
0 |
0.846 |
0 |
0.971 |
0 |
| Gain |
0.971 |
0.517 |
0.294 |
0 |
||||
Gain(humidity) = 0.971
Feature(humidity) = -2/5*log(-2/5) - 3/5*log(3/5) = 0.971(分两组,小于等于70的有2个数据,大于70的有3个数据)
RatioGain(humidity) = 1
Gain(Temperature) = 0.971 - (-log(0.5) * 2/5) = 0.571
Feature(Temperature) = -2/5*log(-2/5)*2 - 1/5*log(1/5) = 1.522(分三组,分别有2、2、1个数据)
RatioGain(Temperature) = 0.375
Gain(Wind) = 0.971 - (3/5*(-1/3*log(1/3)-2/3*log(2/3)) + 2/5( -1/2*log(1/2)-1/2*log(1/2)))= 0.02
Feature(Wind) = 0.971
RatioGain(Wind) = 0.02
因此,程序得到的结果是对的。