机器学习--方差（Variance）与偏差（Bias）的平衡及正则化岭回归

 

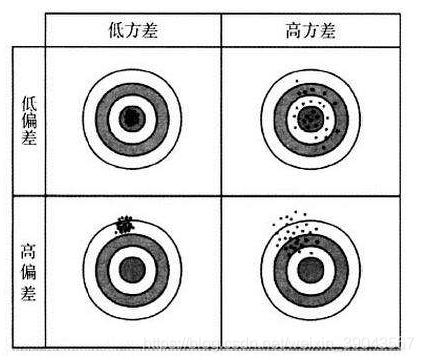
首先理解一下什么是方差和偏差：类比到打靶，低方差就是每次打靶的点都比较集中在某部分，低偏差就是每次打靶都离目标较远。方差就是描述的离散程度，偏差描述的命中程度。

模型的误差：偏差+方差+不可避免的误差（数据本身的噪音）

偏差+方差和算法模型关系密切。导致偏差：如非线性数据使用线性回归，即欠拟合。导致方差：数据的扰动对模型影响很大，即模型学习过多的噪音数据。

kNN 天生高方差，非参数学习通常都是高方差的算法，因为不对数据假设。

线性回归高偏差算法，参数学习通常都是高偏差算法，对数据具有极强的假设。

大多数ML都是有相应的参数，调整相应的方差 和偏差。

kNN中的k，线性回归使用多项式回归（阶数）。

偏差和方差是矛盾的，互相制约的，降低其中一个另一个提高，所以要达到一个平衡，以找到较好的模型。

算法上主要来自方差，解决高方差手段：

1、降低模型复杂度

2、减少数据维度，降噪

3、增加样本数

4、使用验证集

5、模型正则化

模型正则化（Regularization）

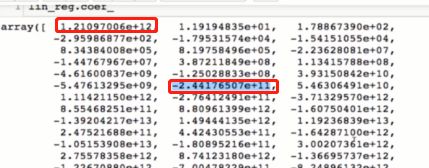
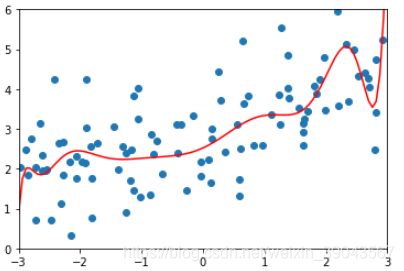
以上是多项式过拟合的情况，途中曲线非常陡峭，造成这种情况的原因是参数（θ）太大，我们可以看一下系数：

模型正则化：限制参数的大小。来解决方差问题  ，怎么来限制呢？？

目标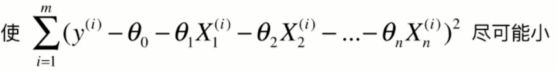：，，如果过拟合的话θ系数会过大。  解决是改变损失函数--》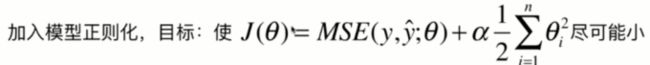

要想使J小，不仅要MSE小，后面的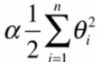也得尽量小。（注意θ0没有加进去，1/2使惯例 加不加都行，方便计算而已，），α是新的超参数，代表在模型正则化下新的损失函数中每一个θ都尽可能小，小的程度占优化整个损失函数的多少，等于0的话相当于没有正则化。

以上的方式就叫做：岭回归(Ridge Regression)

动手实践一下，更清楚明朗：

import numpy as np
import matplotlib.pyplot as plt

#生成实验数据
np.random.seed(42)
x=np.random.uniform(-3.0,3.0,size=100)
X=x.reshape(-1,1)
y=0.5*x+3+np.random.normal(0,1,size=100)

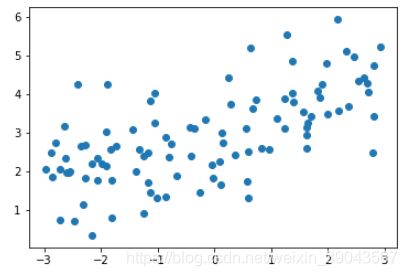
#画个图瞅一瞅
plt.scatter(X,y)

#使用pipeline 进行多项式回归  
from sklearn.pipeline import Pipeline
from sklearn.preprocessing import PolynomialFeatures
from sklearn.linear_model import LinearRegression
from sklearn.preprocessing import StandardScaler

def PolynomialRegression(degree):
    return Pipeline([
        ("poly",PolynomialFeatures(degree=degree)),
        ("std_scaler",StandardScaler()),
        ("lin_reg",LinearRegression())
    ])

#构建训练集、测试集
from sklearn.model_selection import train_test_split
np.random.seed(666)
X_train,X_test,y_train,y_test=train_test_split(X,y)

#进行预测  查看均方差
from sklearn.metrics import mean_squared_error
poly_reg=PolynomialRegression(degree=20)
poly_reg.fit(X_train,y_train)
y_polt_predict=poly_reg.predict(X_test)
mean_squared_error(y_test,y_polt_predict)

167.94010867772357

这个均方差显然是很大的，画个图看看这个模型的预测曲线：

x_plot=np.linspace(-3,3,100).reshape(100,1)
y_plot=poly_reg.predict(x_plot)

plt.scatter(x,y)
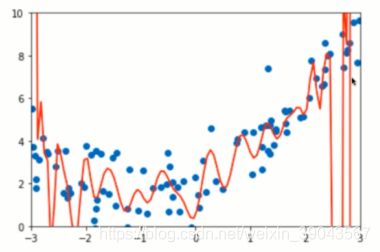
plt.plot(x_plot[:,0],y_plot,color='r')
plt.axis([-3,3,0,6])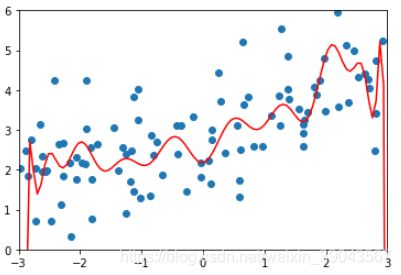

显然出现了过拟合的情况，下面我们就加入使用岭回归的正则化方式进行调整。

首先将绘图构成函数，方便不同模型传入直接画图

def plot_model(model):
    x_plot=np.linspace(-3,3,100).reshape(100,1)
    y_plot=model.predict(x_plot)

    plt.scatter(x,y)
    plt.plot(x_plot[:,0],y_plot,color='r')
    plt.axis([-3,3,0,6])

构建Pipeline，将线性回归变成RidgeRegression

from sklearn.linear_model import Ridge
def RidgeRegression(degree,alpha):
    return Pipeline([
        ("poly",PolynomialFeatures(degree=degree)),
        ("std_scaler",StandardScaler()),
        ("ridge",Ridge(alpha=alpha))
    ])
    

首先α等于很小的情况：

ridge1_reg=RidgeRegression(20,0.0001)
ridge1_reg.fit(X_train,y_train)
y1_pre=ridge1_reg.predict(X_test)
mean_squared_error(y_test,y1_pre)

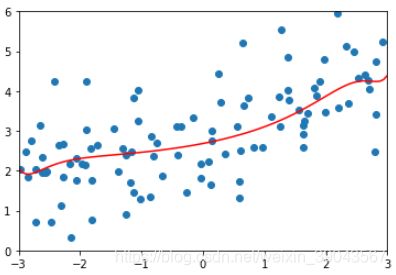
plot_model(ridge1_reg)

结果显示：均方差变得很小，曲线趋于平滑

1.3233492754136291

α等于10的情况：

ridge2_reg=RidgeRegression(20,10)
ridge2_reg.fit(X_train,y_train)
y2_pre=ridge2_reg.predict(X_test)
mean_squared_error(y_test,y2_pre)

plot_model(ridge2_reg)

结果：均方误差变得更小，曲线更趋于平滑

1.1451272194878865

α等于很大的情况：

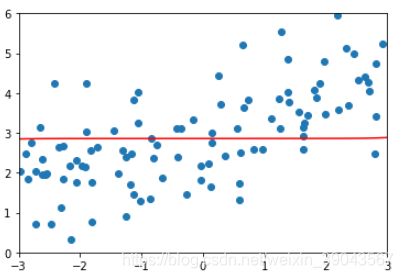
#让alpga等于非常大的情况， 曲线近乎一条曲线
#mse更大了，   正则过头了，损失函数中，尽可能让θi小，α很大的话 θi近乎0，就会出现一下情况
ridge4_reg=RidgeRegression(20,100000)
ridge4_reg.fit(X_train,y_train)
y4_pre=ridge4_reg.predict(X_test)
mean_squared_error(y_test,y4_pre)

plot_model(ridge4_reg)

1.8360988778885547

LASSO:

和岭回归一样也是正则化的一种方式，基本原理和岭回归一样，只不过正则项变成了：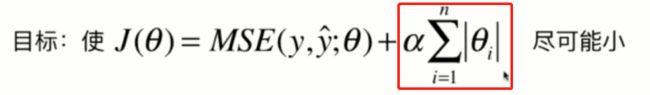

LASSO趋向于使得一部分theta变成0，可以作为特征选择用，因为某个特征的系数θ如果为0的话他在整个函数中就不起作用了。也可能让有用的特征不起作用。岭回归是让θ尽可能的小。