集成学习（机器学习）

集成学习

• Bagging

  实例：

  
  

1. 采样方式

   随机采样（bootsrap）就是从我们的训练集中采集固定个数的样本，但是每采样一个样本后，都将样本放回。也就是说，之前采集到的样本放回后有可能继续被采集到。

2. 集成方式

   Bagging的集合策略也比较简单，对于分类问题，通常使用简单投票法，得到最多票数的类别或者类别之一为最终的模型输出。对于回归问题，通常采用简单平均，对弱学习器得到的回归结果进行算数平均得到最终的模型输出

3. 优缺点

   其主要目的为通过平均降低方差。$Z_1,Z_2,\cdots ,Z_n$的方差为${\delta }^2/n$。采用Bagging策略明显减小模型方差（variance）。

   此方法降低了方差，但由于将多棵决策树的结果进行了平均，这损失了模型的可解释性。同时对于训练集的拟合程度会差一些，也就是模型的偏倚会大一些。

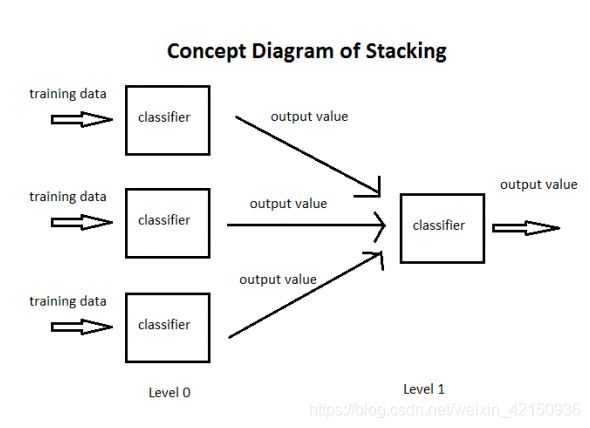
• Stacking

  Stacking就是当用初始训练数据学习出若干个基学习器后，将几个学习期的预测结果作为新的训练集，来学习一个新的学习器

  实例：

  
  

1. 采样方式

   直接使用测试集进行预测

2. 集成方式

   a. 使用交叉验证方式对训练集样本进行训练得到第一层classifier，之后使用classifier对训练集样本进行预测从而得到结果（nm的矩阵,n表示训练集的行数，m代表分类器的个数）
   b. 将第一层的测试结果（nm矩阵）作为输入，对训练集进行训练得到第二层的classifier，则得到第二层classfier

3. 优缺点

   它的平滑性和突出每个基本模型在其中执行的最好的能力，并且抹黑其执行不佳的每个基本模型，所以由于单个模型。当基本模型显著不同时，堆叠是最有效的。

• Boost算法

1. 简介

   Boost(提升)，是指每次我都产生一个弱模型，然后加权累加到总模型中，然后每一步弱预测模型生成的依据都是损失函数的负梯度方向，这样若干步后就可以达到逼近损失函数局部最小值的目的

2. 加法模型

   $$f(x)=\sum _{m=1}^M{\beta }_{m}b(x;{\theta }_m)$$

   其中$b$是基函数，$\beta$是基函数的系数，这就是最终分类器。现在我们的目标是使损失函数的期望取最小值，也就是：
   $$\underset{{\beta }_m,{\theta }_m}{\min }\sum _{i=1}^{N}L(y_i,\sum _{m=1}^M{\beta }_{m}b(x_i;{\theta }_m))$$

   一次性对M个分类器同时进行优化，显然不现实。因此提出了以下的想法：
   $$\underset{{\beta }_m,{\theta }_m}{\min }\sum _{i=1}^{N}L(y_i,f_{m-1}+{\beta }_{m}b(x_i;{\theta }_m))$$

   要使损失函数最小，那就使得新加的一项刚好等于损失函数的负梯度，这样不就使得损失函数的下最快下降了吗，因此就有：

   $${\beta }_{m}b(x;{\theta }_m)=-\lambda \frac{dL(y,f_{m-1})}{df}$$

   此方法只是对提升法的解释，使用时还需要根据具体情况分析

• 处理方法之GDBT

1. 采用平方误差作为损失函数

$$L(y,f_{m-1}(x)+{\beta }_{m}b(x;{\theta }_m))$$
$$(y-f_{m-1}(x)-{\beta }_{m}b(x;{\theta }_m){)}^2$$

2. 数据处理

   上式可以等价于：
   $$({\gamma }_{m-1}-{\beta }_{m}b(x;{\theta }_m){)}^2$$

3. 理解

   以${\gamma }_{m-1}$作为输出，使用X去拟合一个回归树进而形成新的区域划分$R_m$。划分后，将会生成新的区域如$R_{m1},R_{m2},\cdots R_{mj}$,对应的取值为$c_{m1},c_{m2},\cdots c_{mj}$
   $$f_m=f_{m-1}+\sum _{j=1}^m{c}_{mj}I(x\in R_{mj})$$

• Adaboost的原理

3. 简介

   AdaBoost,是英文“Adaptive Bootsing”的缩写。它的自适应在于：前一个基本分类器分错的样本会得到加强，加权后的全体样本再次被用来训练下一个基本分类器。同时，在每一轮转中加入一个新的弱分类器，直到达到某个预定的足够小的错误率或达到预指定的最大迭代次数。

   具体来说，整个Adaboost迭代算法就3步：
   a. 初始化训练数据的权值分布。如果有N个样本，则每个训练样本最开始时都被赋予相同的权值：1/N
   b. 训练弱分类器。具体训练过程中，如果某个样本点已经被准去地分类，那么在构造下一个训练集中，它的权值就被降低；相反，如果某个样本点没有被准确地分类，那么它的权值就得到提高。然后，权值更新过的样本集被用于训练下一个分类器，整个训练过程如此迭代地进行下去。
   c. 将各个训练得到的弱分类器组合成强分类器。各个弱分类器的训练过程结束后，加大分类误差率小的分类器的权重，使其在最终的分类函数中起着较大的决定作用，而降低分类误差较大的弱分类器的权重，使其在最终的分类函数中起着较小的决定作用。换言之，误差率低的弱分类器在最终分类器中的权重较大，否则较小

4. 计算流程

   给定一个训练数据集$T=\{(x_1,y_1),(x_2,y_2),\cdots ,(x_N,y_N)\}$，其中实例$x\in R^n$, $y_i\in Y=\{-1,+1\}$。Adaboost的目的就是从训练集中学习到一系列弱分类器或基本分类器，最后将这些弱分类器组合成为一个强分类器。

   步骤1. 初始化训练数据的权值分布。每个样本最初时都被赋予相同的权值：$1/N$
   $$D_1=(w_{11},w_{12},\cdots ,w_{1N}),w_{1i}=\frac{1}{N},i=1,2,\cdots ,N$$

   步骤2. 进行多轮迭代，用m=1,2,…M代表迭代的轮数

   a. 使用权值分布$D_m$的训练数据集学习，得到基本分类器

   $$G_m:X\to \{-1,1\}$$

   b. 计算$G_m(x)$在训练集上的分类误差率：
   $$e_m=P(G_m(x_i)̸=y_i)=\sum _{i=1}^n{w}_{mi}I(G_m(x_i)̸=y_i)$$
   注：$I(G_m(x_i)̸=y_i)$:不等函数$I$的值为1，相等函数$I$的值为0

   c. 计算G_m(x)的系数
   $$a_m=\frac{1}{2}\log \frac{1-e_m}{e_m}$$
   这里的对数是自然对数。显然$a_m$是$e_m$的单调函数，这里就解释了为什么对于没有正确分类的数据要加大权值

   d. 更新训练集的权值
   $$D_{m+1}=(w_{m+1,1},w_{w+1,2},\cdots ,w_{m+1,N})$$
   $$w_{m+1,i}=\frac{w_{mi}}{Z_m}exp(-{\alpha }_m{y}_i{G}_m(x_i))$$
   这里，$Z_m$是泛化因子
   $$Z_m=\sum _{i=1}^N{w}_{mi}exp(-{\alpha }_m{y}_i{G}_m(x_i))$$
   它使得$D_{m+1}$成为一个概率分布

步骤3. 构建基本分类器的线性组合

$$f(x)=\sum _{m=1}^M{a}_m{G}_m(x)$$
得到最终分类器：
$$G(x)=sign(f(x))=sign(\sum _{m=1}^M{a}_m{G}_m(x))$$

3. 特点

标准的Adaboot算法只适用于二分类，要想让其处理多分类或回归任务还需要对其进行修改

• Adaboost公式推导

1. 损失函数

$$L(y,f(x)=exp[-yf(x)]$$

2. 目标

$$(a_m,G_m(x))=argmi{n}_{a,G}\sum _{i=1}^{N}exp[-y_i(f_{m-1}(x_i)+aG(x_i))]$$

其中$f_{m-1}(x_i)$代表$x_i$在m-1棵树的得分

3. 推导

$$(a_m,G_m(x))=argmi{n}_{a,G}\sum _{i=1}^N{\hat{w}}_{mi}exp[-y_{i}aG(x_i)]$$

其中${\hat{w}}_{mi}=exp[-y_i{f}_{m-1}(x_i)]$。${\hat{w}}_{mi}$既不依赖于$a$也不依赖于$G$，与最小值无关

4. 化简上式的右式可得：

$$e^{-a}\sum _{y_i=G(x_i)}{\hat{w}}_{mi}+e^a\sum _{y_i̸=G(x_i)}{\hat{w}}_{mi}$$

加上两个基础项有:

$$e^{-a}\sum _{y_i=G_m(x)}{\hat{w}}_{mi}+e^a\sum _{y_i̸=G(x_i)}{\hat{w}}_{mi}+e^{-a}\sum _{y_i̸=G(x_i)}{\hat{w}}_{mi}-e^{-a}\sum _{y_i̸=G(x_i)}{\hat{w}}_{mi}$$

等价于
$$(e^a-e^{-a})\sum _{y_i̸=G(x_i)}{\hat{w}}_{mi}+e^{-a}\sum _{i=1}^n{w}^{mi}$$

等价于

$$(e^a-e^{-a})\sum _{i=1}^n{\hat{w}}_{mi}I(y_i̸=G(x_i))+e^{-a}\sum _{i=1}^n{\hat{w}}_{mi}$$

上式中${\hat{w}}_{mi}$是由上次迭代计算得到，当a已知时需要使下面的之最小
$$G_m=arg\underset{G}{\min }\sum _{i=1}^n{\hat{w}}_{mi}I(y_i̸=G(x_i))$$

进一步求$a$使损失函数最小，则有：
$$\frac{\partial L}{\partial a}=(e^a+e^{-a})\sum _{i=1}^n{\hat{w}}_{mi}I(y_i̸=G(x_i))-e^{-a}\sum _{i=1}^n{\hat{w}}_{mi}=0$$

化简可得：

$$e^{2a}\sum _{i=1}^n{\hat{w}}_{mi}I(y_i̸=G(x_i))=\sum _{i=1}^n{\hat{w}}_{mi}-\sum _{i=1}^n{\hat{w}}_{mi}I(y_i̸=G(x_i))$$

进而可得最小参数$a_m$：

$$a_m=\frac{1}{2}log\frac{{\sum }_{i=1}^n{\hat{w}}_{mi}-{\sum }_{i=1}^n{\hat{w}}_{mi}I(y_i̸=G(x_i))}{{\sum }_{i=1}^n{\hat{w}}_{mi}I(y_i̸=G(x_i))}$$

因为错误率为：

$$e_m=\frac{{\sum }_{i=1}^n{\hat{w}}_{mi}I(y_i̸=G(x_i))}{{\sum }_{i=1}^n{\hat{w}}_{mi}}$$

进而计算$a_m$

$$a_m=\frac{1}{2}log\frac{1-e_m}{e_m}$$

根据$w_{mi}=exp(-y_i{f}_{m-1}(x_i))$,更新$w$公式可得：

$$w_{(m+1)i}=exp(-y_i{f}_m(x_i))$$
$$=exp(-y_i(f_{m-1}(x_i)+a_m{G}_m(x_i)))$$
$$=w_{mi}exp(-a_m{y}_i{G}_m(x_i))$$

• Xgboost公式推导

1. 定义损失函数

$$L(y_i,{\hat{y}}_i^t)=\sum _{i=1}^n+L(y_i,{\hat{y}}_i^{t-1}+f_t(x_i))+\Omega (f_t)$$

2. 对定义进行泰勒展开

$$L(y_i,{\hat{y}}_i^t)=\sum _{i=1}^n[L(y_i,{\hat{y}}_i^{t-1})+g_i{f}_t(x)+\frac{1}{2}{h}_i(f_t(x){)}^2]+\Omega (f_t)$$

$$L(y_i,{\hat{y}}_i^t)=\sum _{i=1}^{n}L(y_i,{\hat{y}}_i^{t-1})+\sum _{i=1}^n[g_i{f}_t(x)+\frac{1}{2}{h}_i(f_t(x){)}^2]+\gamma T+\frac{1}{2}\lambda ||w|{|}_2$$

3. 优化损失函数转化为优化以下式子

$$\sum _{i=1}^n{g}_i{f}_t(x)+\frac{1}{2}\sum _{i=1}^n[h_i{w}_i^2+\lambda w_i^2]$$

4. 使用叶子结点表示如下：

$$\sum _{j=1}^T\left[\right(\sum _{i\in I_j}{g}_i)w_j+\frac{1}{2}(\sum _{i\in I_j}{h}_i+\lambda \left)w_i^2\right]+\gamma T$$

5. 优化方法转换为

$$w_j^{\ast }=-\frac{G_j}{H_j+\lambda }$$

其中：$G_j={\sum }_{i\in I_j}{g}_i,H_j={\sum }_{i\in I_j}{h}_i$

损失函数的取值如下：

$$-\frac{1}{2}\sum _{j=1}^T\frac{G_j^2}{H_j+\lambda }+\lambda T$$

6. 贪心算法

$$Gain=\frac{1}{2}[\frac{G_L^2}{H_L+\lambda }+\frac{G_R^2}{H_R+\lambda }-\frac{(G_L+G_R{)}^2}{H_L+H_R+\lambda }]-\lambda T$$