Logistic回归原理分析和实践
Logistic回归原理分析和实践
参考资料:
- 机器学习 周志华
- 统计学习方法 李航
- 一些博客:logistic回归详解,详解最大似然估计(MLE)、最大后验概率估计(MAP),以及贝叶斯公式的理解,逻辑回归(Logistic Regression)-牛顿法求解参数
原理分析
线性回归
这里介绍Logisitic回归首先从线性回归讲起(logistic回归其实就是一种广义的线性回归)。
线性模型(linear model)试图学得一个通过属性的线性组合来进行的预测的函数(假设给定d个属性, x = [ x 1 , x 2 , . . . , x d ] \pmb{x}=[x_1,x_2,...,x_d] xxx=[x1,x2,...,xd]),即:
f ( x ) = w 1 x 1 + w 2 x 2 + . . . + w d x d + b f(x)=w_1x_1+w_2x_2+...+w_dx_d+b f(x)=w1x1+w2x2+...+wdxd+b
写成矩阵形式( w = [ w 1 , w 2 , . . . , w d ] \pmb{w}=[w_1,w_2,...,w_d] www=[w1,w2,...,wd]):
f ( x ) = w T x + b f(x)=\pmb{w^Tx}+b f(x)=wTxwTxwTx+b
“线性回归”(linear regression)试图学得一个线性模型以尽可能准确的预测实值输出。(其求解参数方法在此不做过多介绍)
线性模型虽然简单,但是却有着丰富的变化,假如我们所需要求解的输出可能在指数尺度上变化,那么我们可能需要以下的线性模型:
l n y = w T x + b lny=\pmb{w^Tx}+b lny=wTxwTxwTx+b
这就是“对数线性回归”(log-linear-regression),它实际上是在试图让 e w T x + b e^{\pmb{w^Tx}+b} ewTxwTxwTx+b去逼近 y y y,但是写成上述形式仍是线性回归,实际上已经是在求一种非线性关系。
更一般的,考虑单调可微函数 g ( . ) g(.) g(.),令:
y = g − 1 ( w T x + b ) y=g^{-1}(\pmb{w^Tx}+b) y=g−1(wTxwTxwTx+b)
这样得到模型称为“广义线性模型”(generalized linear model),其中 g ( . ) g(.) g(.)称为“联系函数”(link function),上述对数线性函数就是广义线性函数当 g ( . ) = l n ( . ) g(.)=ln(.) g(.)=ln(.)的一种特例。
逻辑回归
线性回归表现为输入与输出的一种线性关系,而逻辑回归直观上表现了0,1分类的形式(比如预测未来经济增长可能个线性回归问题,但是预测一张图片是猫咪还是狗狗就是一个逻辑回归问题)
但是我们可以使用上述提到的广义线性模型来实现。
考虑二分类任务,其输出标记 y ∈ { 0 , 1 } y\in\left\{ 0,1 \right\} y∈{0,1},而线性回归模型产生的预测值 z = w T x + b z=\pmb{w^Tx}+b z=wTxwTxwTx+b是实值,于是我们只需要将实值z转化为0/1值,可以使用以下的“单位跃迁函数”(unit-step function)
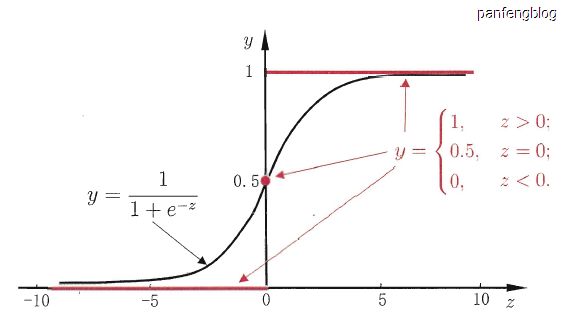
f ( x ) = { 0 , z < 0 0 / 1 , z = 0 1 , z > 0 f(x)=\left\{ \begin{aligned} 0,\,\,\,z<0 \\ 0/1,\,\,\,z=0 \\ 1,\,\,\,z>0 \end{aligned} \right. f(x)=⎩⎪⎨⎪⎧0,z<00/1,z=01,z>0
即若预测值大于0就判正例,小于0则判反例,等于0可任意判别。
但是单位跃迁函数不连续,因此不能直接用作广义线性模型的 g ( . ) g(.) g(.),因此我们希望找到一定程度上近似单位跃迁函数的函数,并且希望它满足单调可微,对数几率函数(Logistic function)正好就满足(如下)。
y = 1 1 + e − z y=\cfrac{1}{1+e^{-z}} y=1+e−z1
可以从上图中看出,对数几率函数是一种“Sigmoid函数”(即形如S的函数,对率函数就是其中最重要的代表),将对数几率函数带入广义线性模型可以得到下式:
y = 1 1 + e w T x + b y=\cfrac{1}{1+e^{\pmb{w^Tx}+b}} y=1+ewTxwTxwTx+b1
将上式进行一些变形:
l n y 1 − y = w T x + b ln\cfrac{y}{1-y}=\pmb{w^Tx}+b ln1−yy=wTxwTxwTx+b
若将 y y y视为样本 x \pmb{x} xxx作为正例的可能性,则 1 − y 1-y 1−y是其反例可能性,二者的比值 y 1 − y \cfrac{y}{1-y} 1−yy称为几率(odds),反应了样本 x \pmb{x} xxx作为正例的相对可能性,对几率取对数得到“对数几率”(log odds,亦称logit) l n y 1 − y ln\cfrac{y}{1-y} ln1−yy
由此可以看出逻辑回归实际上就是在用线性回归模型的预测结果去逼近真实标记的对数几率,因此其对应的模型称为“对数几率回归”(logistic regression),逻辑回归就是其音译的结果,中文“逻辑”和“logistic”的含义相差甚远。值得注意的是,虽然它的名字里面是“回归”,但它实际上是一种分类学习方法。
逻辑回归参数的求解
一些符号的说明: a i = 1 1 + e w T x i + b a_i=\cfrac{1}{1+e^{\pmb{w^Tx_i}+b}} ai=1+ewTxiwTxiwTxi+b1, z i = w T x i + b z_i=\pmb{w^Tx_i}+b zi=wTxiwTxiwTxi+b,学习率: α \alpha α
1.损失函数
我们通过“极大似然法”来估计参数 w \pmb{w} www和 b b b,
我们首先定义最大似然函数(认为各个样本之间是相对独立的),
l ( w , b ) = ∏ i = 1 m p ( y i ∣ x i ; w , b ) = ∏ i = 1 m a i y i ( 1 − a i ) 1 − y i l(\pmb{w},b)=\prod_{i=1}^{m}p(y_i|\pmb{x_i};\pmb{w},b)=\prod_{i=1}^{m}a^{y_i}_i(1-a_i)^{1-y_i} l(www,b)=i=1∏mp(yi∣xixixi;www,b)=i=1∏maiyi(1−ai)1−yi
如果使用一般最大似然会出现概率连乘的表达式,容易造成数值溢出,因此在采用对数似然(并且更容易进行求导),将连乘结果转化为累加:
l n l ( w , b ) = ∑ i = 1 m l n p ( y ∣ x ; w , b ) = ∑ i = 1 m y i l n a i + ( 1 − y i ) l n ( 1 − a i ) ln \, l(\pmb{w},b)=\sum_{i=1}^{m}ln\,p(y|\pmb{x};\pmb{w},b)=\sum_{i=1}^{m}y_i lna_i+(1-y_i)ln(1-a_i) lnl(www,b)=i=1∑mlnp(y∣xxx;www,b)=i=1∑myilnai+(1−yi)ln(1−ai)
我们定义以下的损失函数:
J ( w , b ) = − l n l ( w , b ) = − ( ∑ i = 1 m y i l n a i + ( 1 − y i ) l n ( 1 − a i ) ) J(\pmb{w},b)=-ln \, l(\pmb{w},b)=-(\sum_{i=1}^{m}y_i lna_i+(1-y_i)ln(1-a_i)) J(www,b)=−lnl(www,b)=−(i=1∑myilnai+(1−yi)ln(1−ai))
之前的似然函数是取最大值的,我们定义的损失函数等于对数似然的相反数,所以损失函数是需要取最小值的(所以对应的是梯度下降法,你可能也听说过梯度上升法,其实是一回事,只是损失函数的定义不同罢了)。
2.1梯度下降法
对于一个样本,使用链式规则,依次求导:
∂ J ∂ a i = − y i a i + 1 − y i 1 − a i \cfrac{\partial J}{\partial a_i}=-\cfrac{y_i}{a_i}+\cfrac{1-y_i}{1-a_i} ∂ai∂J=−aiyi+1−ai1−yi
∂ J ∂ z i = ∂ J ∂ a i ∂ a i ∂ z i = a i − y i \cfrac{\partial J}{\partial z_i}=\cfrac{\partial J}{\partial a_i}\cfrac{\partial a_i}{\partial z_i}=a_i-y_i ∂zi∂J=∂ai∂J∂zi∂ai=ai−yi
∂ J ∂ w = ∂ J ∂ z i ∂ z i ∂ w = x i ( a i − y i ) \cfrac{\partial J}{\partial \pmb{w}}=\cfrac{\partial J}{\partial z_i}\cfrac{\partial z_i}{\partial \pmb{w}}=\pmb{x_i}(a_i-y_i) ∂www∂J=∂zi∂J∂www∂zi=xixixi(ai−yi)(注:这里求出的导数是一个 1xd 的向量)
∂ J ∂ b = ∂ J ∂ z i ∂ z i ∂ b = a i − y i \cfrac{\partial J}{\partial b}=\cfrac{\partial J}{\partial z_i}\cfrac{\partial z_i}{\partial b}=a_i-y_i ∂b∂J=∂zi∂J∂b∂zi=ai−yi
对于m个样本,只需要求平均即可:
∂ J ∂ w = 1 m ∑ i = 1 m x i ( a i − y i ) \cfrac{\partial J}{\partial \pmb{w}}=\cfrac{1}{m}\sum_{i=1}^{m}\pmb{x_i}(a_i-y_i) ∂www∂J=m1i=1∑mxixixi(ai−yi)
∂ J ∂ b = 1 m ( a i − y i ) \cfrac{\partial J}{\partial b}=\cfrac{1}{m}(a_i-y_i) ∂b∂J=m1(ai−yi)
然后更新 w \pmb{w} www和 b b b
w : = w − α ∂ J ∂ w = w − α 1 m ∑ i = 1 m x i ( a i − y i ) \pmb{w}:=\pmb{w}-\alpha \cfrac{\partial J}{\partial \pmb{w}}=\pmb{w}-\alpha \cfrac{1}{m}\sum_{i=1}^{m}\pmb{x_i}(a_i-y_i) www:=www−α∂www∂J=www−αm1i=1∑mxixixi(ai−yi)
b : = b − α ∂ J ∂ b = b − α 1 m ∑ i = 1 m ( a i − y i ) b:=b-\alpha \cfrac{\partial J}{\partial b}=b-\alpha \cfrac{1}{m}\sum_{i=1}^{m}(a_i-y_i) b:=b−α∂b∂J=b−αm1i=1∑m(ai−yi)
2.2 牛顿法
和梯度下降法类似,都是通过迭代算法来实现的。
首先我们来看这么一个问题, f ( x ) = 0 f(x)=0 f(x)=0有近似根 x k x_k xk,那么 f ( x ) f(x) f(x)在点 x k x_k xk处的泰勒展开式表示为: f ( x ) ≈ f ( x k ) + f ′ ( x k ) ( x − x k ) f(x)\approx f(x_k) + f'(x_k)(x-x_k) f(x)≈f(xk)+f′(xk)(x−xk)
令 f ( x ) = 0 f(x)=0 f(x)=0,那么就有 f ( x k ) + f ′ ( x − x k ) = 0 f(x_k)+f'(x-x_k)=0 f(xk)+f′(x−xk)=0,由此就可求解 x = x k − f ( x k ) f ′ ( x k ) x=x_k-\cfrac{f(x_k)}{f'(x_k)} x=xk−f′(xk)f(xk)
对于凸函数而言,这样的一次迭代过程就会进一步的接近极小值,直观理解可以查看下图:
由于我们的损失函数是一个高阶可导的连续凸函数(令 β = [ w ∣ b ] \pmb{\beta}=[\pmb{w}|b] βββ=[www∣b]),所以我们令上述的 f ( x ) = J ′ ( β ) f(x)=J'(\pmb{\beta}) f(x)=J′(βββ),当 J ′ ( β ) = 0 J'(\pmb{\beta})=0 J′(βββ)=0时即为最优解,所以我们就能够这样来更新参数: β = β − ∂ J ∂ β ( ∂ 2 J ∂ β ∂ β T ) − 1 \pmb{\beta} = \pmb{\beta}-\cfrac{\partial J}{\partial \pmb{\beta}} (\cfrac{\partial^2 J}{\partial \pmb{\beta}\partial \pmb{\beta^T}})^{-1} βββ=βββ−∂βββ∂J(∂βββ∂βTβTβT∂2J)−1
这就是牛顿法,其中 H = ( ∂ 2 J ∂ β ∂ β T ) − 1 H=(\cfrac{\partial^2 J}{\partial \pmb{\beta}\partial \pmb{\beta^T}})^{-1} H=(∂βββ∂βTβTβT∂2J)−1被称为黑塞矩阵(Hessian Matrix),由于其不一定可逆(并且求逆的计算量比较大),所以一般使用的时拟牛顿法,拟牛顿法在这就不过多介绍了。(实践中牛顿法和拟牛顿法都没有使用)
Logistic回归实践
逻辑回归实践使用是Pima印第安人数据集,该数据集最初来自国家糖尿病/消化/肾脏疾病研究所。数据集的目标是基于数据集中包含的某些诊断测量来诊断性的预测 患者是否患有糖尿病。整个实践过程没有使用任何的机器学习库,需要完整代码可以点击这里,点击这里。
python3开发环境说明:
numpy:1.15.4matplotlib:2.2.3
1. 加载数据
数据集(Pima.csv)共有9个特征,分别如下:
- Pregnancies:怀孕次数
- Glucose:葡萄糖
- BloodPressure:血压
- SkinThickness:皮层厚度
- Insulin:胰岛素 2小时血清胰岛素
- BMI:体重指数 (体重/身高)^2
- DiabetesPedigreeFunction:糖尿病谱系功能
- Age:年龄 (岁)
- Outcome:类标变量 (0或1)
将数据加载到矩阵中(将特征和最终的结果分开保存)
import numpy as np
import matplotlib.pyplot as plt
pimaForm = np.loadtxt('Pima.csv', dtype=np.float64, delimiter=',') # 加载整个表格
data = pimaForm[:,:8].T # 数据部分
label = pimaForm[:,8:].astype(np.int16) # 标签部分
print(data.shape, label.shape)
输出结果:
(8, 768) (768, 1)
2. 数据预处理
2.1 缺失值处理
我们简单的直接使用均值填充了缺失值
dataMean = data.mean(axis=1) # 计算均值,用于缺失值填充
dataStd = data.std(axis=1) # 计算标准差,用于后续数据处理
for i in range(data.shape[0]):
for j in range(data.shape[1]):
if data[i][j] == 0: # 出现缺失值就用均值填充
data[i][j] = dataMean[i]
2.2 输出归一化
认为输入数据为正态分布,然后进行归一化处理
data = ((data.T - dataMean)/dataStd).T # 使用z-score标准化方法
2.3 数据集划分
训练集和测试集按照 5:1 的比例划分
testData = data[:,:128]
testLabel = label[:128]
trainData = data[:,128:]
trainLabel = label[128:]
print(testData.shape, testLabel.shape, trainData.shape, trainLabel.shape)
输出结果:
(8, 128) (128, 1) (8, 640) (640, 1)
3. 初始化参数
对参数进行随机初始化:
def initParameter(feature_num):
w = np.random.rand(1, feature_num) # w:1xfeature_num, 用0-1随机数初始化
b = 0 # b初始化为0
return w,b
test_w, test_b = initParameter(8) # 测试一下
print(test_w.shape, test_b)
输出结果:
(1, 8) 0
4. 向前传播
先计算线性模型,然后再带入sigmoid函数。
def forward(data, w, b):
z = np.dot(w, data) # 计算线性部分
a = 1/(1+np.exp(-z)) # 计算预测结果
return a.T
a = forward(trainData, test_w, test_b)
print(a.shape)
输出结果:
(640, 1)
5. 梯度下降
反向求导过程
def gradDescent(w, b, x , y, a, learning_rate):
w = w - learning_rate * np.dot(x, a-y).T / a.shape[0] # 更新参数w
b = b - learning_rate * (a-y).sum(axis=0)[0] # 更新参数b
return w,b
test_w2, test_b2 = gradDescent(test_w, test_b, trainData, trainLabel, a, 0.01)
print(test_w2.shape, test_b2)
输出结果:
(1, 8) -1.3182942043705952
6. 开始训练
就是不断循环向前传播和梯度下降的一个过程:
w, b = initParameter(8) # 测试一下
cost = []
for i in range(200):
a = forward(trainData, w, b)
w, b = gradDescent(w, b, trainData, trainLabel, a, 0.4)
cost.append((-(trainLabel*np.log(a)+(1-trainLabel)*np.log(1-a))).sum(axis = 0)[0]/a.shape[0])
plt.plot(cost)
输出结果:
然后进行预测
testPred = (forward(testData, w, b)>0.5).astype(np.int16)
print("测试集正确率:"+str((testPred==testLabel).astype(np.int16).reshape(-1).sum()/testPred.shape[0]))
输出结果:
测试集正确率:0.734375