基于LSTM的Chatbot实例(4) — 基于SGD的模型参数训练及优化

一、SGD基本知识

　　前几篇文章中已经介绍了我们的seq2seq模型使用均方误差作为损失函数，使用SGD算法（随机梯度下降）算法来训练模型参数，实例中代码如下：

net = tflearn.regression(real_output_sequence, optimizer='sgd', learning_rate=0.1, loss='mean_square')

　　大多数机器学习任务最后都涉及到优化算法（调整模型参数以最小化损失函数），仅使用梯度的优化算法称为一阶优化算法，如梯度下降（GD）算法。使用Hessian矩阵（二阶偏导矩阵）的优化算法称为二阶优化算法。总的来说一阶收敛算法只考虑了局部的最优，每次只从你当前所处位置选一个坡度最大的方向走一步，牛顿法在选择方向时，不仅会考虑坡度是否够大，还会考虑你走了一步之后，坡度是否会变得更大。从几何上说，牛顿法就是用一个二次曲面去拟合你当前所处位置的局部曲面，而梯度下降法是用一个平面去拟合当前的局部曲面，通常情况下，二次曲面的拟合会比平面更好，所以牛顿法选择的下降路径会更符合真实的最优下降路径，如下图所示。虽然牛顿法更快收敛到全局或局部最优解，但是迭代的每一步都需要求解目标函数的Hessian矩阵（元素数量是参数数量的平方）的逆矩阵，计算比较复杂（ O(k3) O ( k 3 ) ）。

因此，在机器学习中经常使用的是梯度下降优化方法，其常有以下三种迭代思路：

• 批量梯度下降（Batch gradient descent）：是一种对参数的update进行累积，然后批量更新的一种方式。这种算法很慢，并且对于大的数据集并不适用；并且使用这种算法，我们无法在线更新参数。
• 随机梯度下降（Stochastic gradient descent）：是一种对参数随着样本训练，一个一个的及时update的方式。这种方法迅速并且能够在线使用；但是它频繁的更新参数会使得目标函数波动很大。
• 小批量梯度下降（Mini-batch gradient descent）：吸取了BGD和SGD的优点，每次选择一小部分样本进行训练

这里选用的SGD优化方法，其最基本的迭代更新算法如下（参考文献【2】）：

Fig1-1 SGD 迭代算法

二、tensorflow中优化的SGD

tensorflow中使用SGD训练regression模型的关键代码如下：

# @File    : tflean.layers.estimator.py

def regression(incoming, placeholder='default', optimizer='adam',
               loss='categorical_crossentropy', metric='default',
               learning_rate=0.001, dtype=tf.float32, batch_size=64,
               shuffle_batches=True, to_one_hot=False, n_classes=None,
               trainable_vars=None, restore=True, op_name=None, 
               validation_monitors=None, validation_batch_size=None, name=None):
    """ Regression.

    The regression layer is used in TFLearn to apply a regression (linear or
    logistic) to the provided input. It requires to specify a TensorFlow
    gradient descent optimizer 'optimizer' that will minimize the provided
    loss function 'loss' (which calculate the errors). A metric can also be
    provided, to evaluate the model performance."""

    tr_op = TrainOp(loss=loss,
                    optimizer=optimizer,
                    metric=metric,
                    trainable_vars=tr_vars,
                    batch_size=batch_size,
                    shuffle=shuffle_batches,
                    step_tensor=step_tensor,
                    validation_monitors=validation_monitors,
                    validation_batch_size=validation_batch_size,
                    name=op_name)

    tf.add_to_collection(tf.GraphKeys.TRAIN_OPS, tr_op)

# @File    : tflean.helpers.trainer.py

class TrainOp(object):
    def initialize_training_ops(self, i, session, tensorboard_verbose,
                                clip_gradients):
        """ initialize_training_ops.

        Initialize all ops used for training. Because a network can have
        multiple optimizers, an id 'i' is allocated to differentiate them.
        This is meant to be used by `Trainer` when initializing all train ops."""
        ... 
        ...
        # Creating the accuracy moving average, for better visualization.
        if self.metric is not None:
            self.acc_averages = \
                tf.train.ExponentialMovingAverage(0.9, self.training_steps,
                                                  name='moving_avg')
            acc_avg_op = self.acc_averages.apply([self.metric])
        else:
            acc_avg_op = tf.no_op()

        # Compute total loss, which is the loss of all optimizers plus the
        # loss of all regularizers. Then, we summarize those losses for
        # visualization in Tensorboard.
        with tf.name_scope(self.name):
            lss = [self.loss] + tf.get_collection(tf.GraphKeys.REGULARIZATION_LOSSES)
            total_loss = tf.add_n(lss, name="Total_Loss")
            loss_avg_op = summaries.add_loss_summaries(
                total_loss,
                self.loss,
                regul_losses_collection_key=tf.GraphKeys.REGULARIZATION_LOSSES,
                name_prefix=self.scope_name,
                summaries_collection_key=self.name + "_training_summaries",
                exp_moving_avg=0.9,
                ema_num_updates=self.training_steps)

            # Compute gradients operations
            with tf.control_dependencies([loss_avg_op, acc_avg_op]):
                self.grad = tf.gradients(total_loss, self.train_vars)
                if clip_gradients > 0.0:
                    self.grad, self.grad_norm = \
                        tf.clip_by_global_norm(self.grad, clip_gradients)

            self.grad = list(zip(self.grad, self.train_vars))
            self.apply_grad = self.optimizer.apply_gradients(
                    grads_and_vars=self.grad,
                    global_step=self.training_steps,
                    name="apply_grad_op_" + str(i))

            # Create other useful summary (weights, grads, activations...)
            # according to 'tensorboard_verbose' level.
            self.create_summaries(tensorboard_verbose)

            # Track the moving averages of trainable variables
            if self.ema > 0.:
                var_averages = tf.train.ExponentialMovingAverage(
                        self.ema, self.training_steps)
                var_averages_op = var_averages.apply(self.train_vars)

                with tf.control_dependencies([var_averages_op]):
                    with tf.control_dependencies([self.apply_grad]):
                        self.train = tf.no_op(name="train_op_" + str(i))
            else:
                with tf.control_dependencies([self.apply_grad]):
                    self.train = tf.no_op(name="train_op_" + str(i))

用tensorboard可视化出tensorflow中SGD模块的计算图如下：

Fig2-1 SGD in tensorflow
　　其中 绿色框1是梯度计算图。 绿色框2使用了 滑动平均来控制模型更新的速率，使模型较为平滑的更新。 绿色框3中使用 梯度剪裁来避免梯度膨胀 绿色框4是更新权重参数，同时 指数衰减调整学习率。下面将分别介绍:

＃2.1 梯度计算图

梯度计算图基本上是之前使用seq2seq模型计算图的逆序（自行联想复合函数的求导过程），下面仅给出BasicLSTMCell的梯度计算图，可以和上一篇中的BasicLSTMCell计算图形成对比如下：

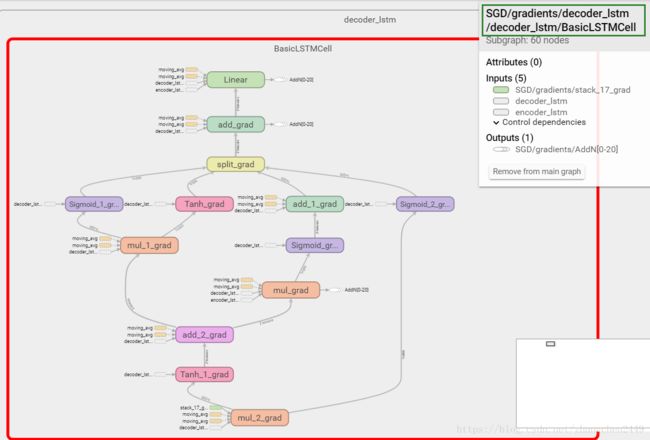
Fig 2-2 BasicLSTMCell gradient 计算图
Fig 2-3 BasicLSTMCell计算图
代码可参考截取如下：

# @File    : tflean.helpers.trainer.py

class TrainOp(object):
    def initialize_training_ops(self, i, session, tensorboard_verbose,
                                clip_gradients):
            ...
            ...  
            with tf.control_dependencies([loss_avg_op, acc_avg_op]):
                self.grad = tf.gradients(total_loss, self.train_vars)

＃2.2 滑动平均

　　在训练神经网络时，不断保持和更新每个参数的滑动平均值，在验证和测试时，参数的值使用其滑动平均值，能有效提高神经网络的准确率。图Fig 2-1中绿色框2中对应的tensorflow源码为：

self.acc_averages = tf.train.ExponentialMovingAverage(0.9, self.training_steps, name='moving_avg')
acc_avg_op = self.acc_averages.apply([self.metric])

　　其中ExponentialMovingAverage对每一个变量都会维护一个影子变量( shadow_variable s h a d o w _ v a r i a b l e )，它的初始值为对应变量的值，每次运行变量更新时，影子变量的值很更新为

shadow_variable−=(1−decay)∗(shadow_variable−variable) s h a d o w _ v a r i a b l e − = ( 1 − d e c a y ) ∗ ( s h a d o w _ v a r i a b l e − v a r i a b l e )
　　其中衰减变量 decay d e c a y 随迭代步数 num_updates n u m _ u p d a t e s 更新为：
min(decay,(1+num_updates)/(10+num_updates)) m i n ( d e c a y , ( 1 + n u m _ u p d a t e s ) / ( 10 + n u m _ u p d a t e s ) )
　　在tensorboard中计算图如下：

Fig2-4 滑动平均

＃2.3 梯度剪裁

　　Gradient Clipping的引入是为了处理梯度爆炸（gradient explosion）和梯度消失（exploding gradient）的问题【参考On the difficulty of training Recurrent Neural Networks】。当在一次迭代中权重的更新过于迅猛的话，很容易导致loss divergence。Gradient Clipping的直观作用就是让权重的更新限制在一个合适的范围。图Fig 2-1中绿色框３中对应的tensorflow源码为：

if clip_gradients > 0.0:
      self.grad, self.grad_norm = tf.clip_by_global_norm(self.grad, clip_gradients)

　　其clipping策略为对待更新的每个变量 t_list[i] t _ l i s t [ i ] 按如下形式更新：

t_list[i]=t_list[i]∗clip_norm/max(global_norm,clip_norm) t _ l i s t [ i ] = t _ l i s t [ i ] ∗ c l i p _ n o r m / m a x ( g l o b a l _ n o r m , c l i p _ n o r m )
　　其中 global_norm g l o b a l _ n o r m 计算如下：
global_norm=∑i∈t_listl2_norm(t)2−−−−−−−−−−−−−−−−√ g l o b a l _ n o r m = ∑ i ∈ t _ l i s t l 2 _ n o r m ( t ) 2
　　算法源码如下：

def clip_by_global_norm(t_list, clip_norm, use_norm=None, name=None):
  """Clips values of multiple tensors by the ratio of the sum of their norms."""
  if (not isinstance(t_list, collections.Sequence)
      or isinstance(t_list, six.string_types)):
    raise TypeError("t_list should be a sequence")
  t_list = list(t_list)
  if use_norm is None:
    use_norm = global_norm(t_list, name)

  with ops.name_scope(name, "clip_by_global_norm",
                      t_list + [clip_norm]) as name:
    # Calculate L2-norm, clip elements by ratio of clip_norm to L2-norm
    scale = clip_norm * math_ops.minimum(
        1.0 / use_norm,
        constant_op.constant(1.0, dtype=use_norm.dtype) / clip_norm)

    values = [
        ops.convert_to_tensor(
            t.values if isinstance(t, ops.IndexedSlices) else t,
            name="t_%d" % i)
        if t is not None else t
        for i, t in enumerate(t_list)]

    values_clipped = []
    for i, v in enumerate(values):
      if v is None:
        values_clipped.append(None)
      else:
        with ops.colocate_with(v):
          values_clipped.append(
              array_ops.identity(v * scale, name="%s_%d" % (name, i)))

def global_norm(t_list, name=None):
  """Computes the global norm of multiple tensors.  """
  if (not isinstance(t_list, collections.Sequence)
      or isinstance(t_list, six.string_types)):
    raise TypeError("t_list should be a sequence")
  t_list = list(t_list)
  with ops.name_scope(name, "global_norm", t_list) as name:
    values = [
        ops.convert_to_tensor(
            t.values if isinstance(t, ops.IndexedSlices) else t,
            name="t_%d" % i)
        if t is not None else t
        for i, t in enumerate(t_list)]
    half_squared_norms = []
    for v in values:
      if v is not None:
        with ops.colocate_with(v):
          half_squared_norms.append(gen_nn_ops.l2_loss(v))

    half_squared_norm = math_ops.reduce_sum(array_ops.stack(half_squared_norms))

    norm = math_ops.sqrt(
        half_squared_norm *
        constant_op.constant(2.0, dtype=half_squared_norm.dtype),
        name="global_norm")

  return norm

在tensorboard中的计算图如下：

＃2.4 更新权重

　　在计算了梯度（2.1节）　，并对其进行滑动平均（2.2节）和梯度剪裁（2.3节）后。接下来就可以运用图Fig 1-1中的迭代公式对模型参数进行迭代。如下图所示分别对encoder_lstm和decoder_lstm中的权重（Matrix）和偏置（Bias）进行迭代更新：


代码不再赘述，这里提一下，在tflearn的SGD源码中，学习率learning_rate是指数衰减的，对应源码如下：

class SGD(Optimizer):
    """ Stochastic Gradient Descent.

    SGD Optimizer accepts learning rate decay. When training a model,
    it is often recommended to lower the learning rate as the training
    progresses. The function returns the decayed learning rate.  It is
    computed as:

    ```python
    decayed_learning_rate = learning_rate *
                          decay_rate ^ (global_step / decay_steps)
    ```
    """

    def build(self, step_tensor=None):
        self.built = True
        if self.has_decay:
            if not step_tensor:
                raise Exception("Learning rate decay but no step_tensor "
                                "provided.")
            self.learning_rate = tf.train.exponential_decay(
                self.learning_rate, step_tensor,
                self.decay_step, self.lr_decay,
                staircase=self.staircase)
            tf.add_to_collection(tf.GraphKeys.LR_VARIABLES, self.learning_rate)
        self.tensor = tf.train.GradientDescentOptimizer(
            learning_rate=self.learning_rate,
            use_locking=self.use_locking,
            name=self.name)

　　至此，基于LSTM的Chatbot实例的模型创建，训练及优化部分都介绍完毕。写一篇将模型训练过程中参数迭代情况，以及损失函数Loss变化等指标展示出来。此外还将展示已训练好的模型在测试集合上的拟合效果。

3.参考文献：

【1】Stochastic Gradient Descent Tricks
【2】Deep Learning Book
【3】Machine Learning优化算法
【4】On the difficulty of training Recurrent Neural Networks
【5】Adam: A Method for Stochastic Optimization