R语言学习：泰坦尼克号生存预测

将一部分泰坦尼克号上的乘客数据（包括是否生还）作为训练集，对测试集中的的乘客生还情况进行预测。

导入所用的包

library(randomForest)
library(dplyr)
library(ggplot2)
library(mice)

导入数据

从csv中分别导入训练集和测试集数据

train = read.csv("train.csv",header = T,stringsAsFactors = F） 
test = read.csv("test.csv",header = T,stringsAsFactors = F)

data = bind_rows(train,test)
str(data)

 

'data.frame': 1309 obs. of  12 variables:
 $ PassengerId: int  1 2 3 4 5 6 7 8 9 10 ...
 $ Survived   : int  0 1 1 1 0 0 0 0 1 1 ...
 $ Pclass     : int  3 1 3 1 3 3 1 3 3 2 ...
 $ Name       : chr  "Braund, Mr. Owen Harris" "Cumings, Mrs. John Bradley (Florence Briggs Thayer)" "Heikkinen, Miss. Laina" "Futrelle, Mrs. Jacques Heath (Lily May Peel)" ...
 $ Sex        : chr  "male" "female" "female" "female" ...
 $ Age        : num  22 38 26 35 35 NA 54 2 27 14 ...
 $ SibSp      : int  1 1 0 1 0 0 0 3 0 1 ...
 $ Parch      : int  0 0 0 0 0 0 0 1 2 0 ...
 $ Ticket     : chr  "A/5 21171" "PC 17599" "STON/O2. 3101282" "113803" ...
 $ Fare       : num  7.25 71.28 7.92 53.1 8.05 ...
 $ Cabin      : chr  "" "C85" "" "C123" ...

 

 $ Embarked   : chr  "S" "C" "S" "S" ...

将部分变量转化为因子类型

data[,c(1,2,3,5,12)] = lapply(data[,c(1,2,3,5,12)], FUN = as.factor)

 

总结变量有： 

PassengerId: 乘客的唯一编号

Survived   : 生还情况，生还为1，死亡为0

Pclass     : 舱位，1是最高等，3是最低等

 

Name :  姓名
Sex     : 性别
Age    : 年龄
SibSp     : 同船的兄弟姐妹或配偶
Parch     : 同船的父母或子女
Ticket     : 船票信息
Fare       :  乘客票价
Cabin     : 客舱编号

 

Embarked   : 登船地点，C,S,Q分别代表三个不同地点

缺失值处理

summary(data)

查看数据总体情况，发现Survived（生存情况）存在418个缺失值，是由于测试集中缺少这一预测变量；Age（年龄）存在263个缺失值，缺失值较多；Fare存在两个缺失值；Embarked存在2个缺失值。

data[which(is.na(data$Fare)),1]

发现是第1044位乘客缺少Fare值

data[1044,3]

查看该乘客的舱位等级，发现是3，最低等，故可以考虑用3等舱的票价中位数对该值进行插补。

data1 = data[-1044,]
data_Pclass3_Fare = data1[which(data1$Pclass == 3),10]
median(data_Pclass3_Fare)
data[1044,"Fare"] = median(data_Pclass3_Fare)

发现Embarked缺失值为“”，故将缺失值改为NA，并找出缺失Embarked值的乘客

data$Embarked[data$Embarked == ""] = NA
data[which(is.na(data$Embarked)),1]

发现是第62位，830位乘客缺少Embarked值

data[c(62,830),c(1,3,10)]

观察他们的舱位及票价情况：

    PassengerId Pclass Fare
62           62      1   80

830         830      1   80

两名乘客都是1等舱且票价都为80，找出1等舱的乘客的登船地点以及票价的中位数

data2 = data[which(data$Pclass == 1),]
summarise(group_by(data2,Embarked),mfare = median(Fare),n())

  Embarked   mfare `n()`
     
1        C 76.7292   141
2        Q 90.0000     3
3        S 52.0000   177

4     80.0000     2

可以看到在C处登船的1等舱的乘客的票价中位数为76.7292，与缺失值的票价80最相似，故选择C插补Embarked的两个缺失值

data[c(62,830),"Embarked"] = "C"

针对缺失Age的观测值，由于Age不是因子变量且缺失值较多，考虑用回归法进行插补。首先提取行号，分别将Age存在以及缺失的观测值放到两个数据集中

sub = which(is.na(data$Age) == T)
data_Age = data[-sub,]
data_No_Age = data[sub,]

建立Age与其他变量的回归模型进行插补

lm = lm(Age~Pclass+Sex+SibSp+Parch+Fare+Embarked,data = data_Age)
Age_predict = predict(lm,newdata = data_No_Age)
data[sub,"Age"] = round(Age_predict,0）

探索性分析

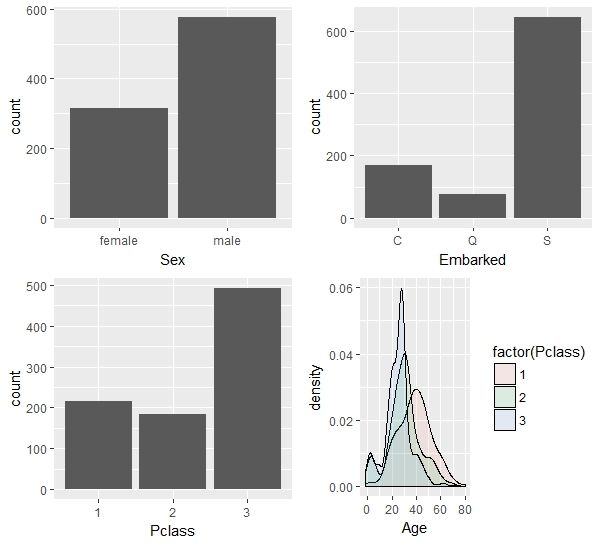
根据图像观察数据总体分布情况

可以得知乘客中男性人数要多于女性，三个地点中S地的乘客最多。在不同等级的仓位分布方面，3等舱是最多的，也符合穷人较多的社会现实，头等舱和二等舱人数相差不大。根据年龄与舱位等级的分布密度图，随着舱位等级增大，年龄分布变老，说明有钱人年龄要比穷人年龄大，也符合常识。

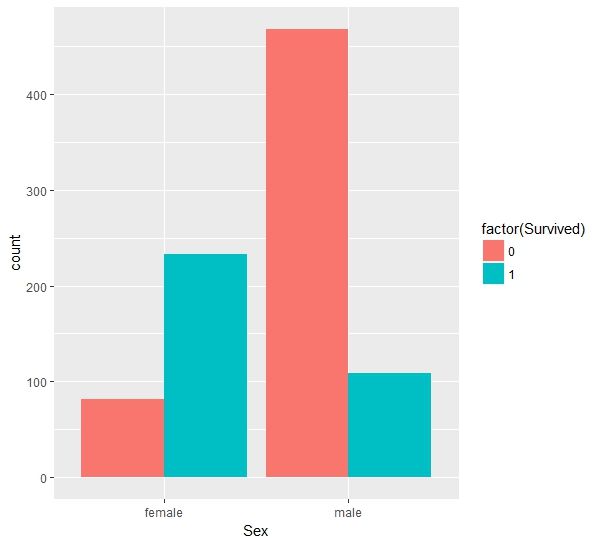
根据性别与生存情况的直方图，可以看出女性获救的比例要明显高于男性，电影中遇到灾难时也是让女人先登船。

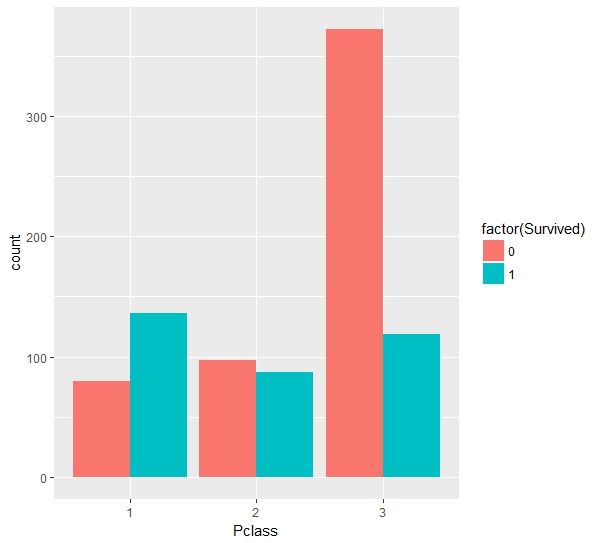
同时也看到，等级越高的舱位获救的比例越高，说明遇到灾难的时候符合让有钱人先走的定律。

建立模型

使用随机森林建立模型，从实际出发，考虑到姓名、船票与客舱编号对实际是否存活影响不大，在建立模型时不考虑这三个因素。

首先将训练集和测试集分开

train = data[1:891,]
test = data[892:1309,]

根据训练集建立随机森林模型并绘出模型误差与决策树数量的关系图

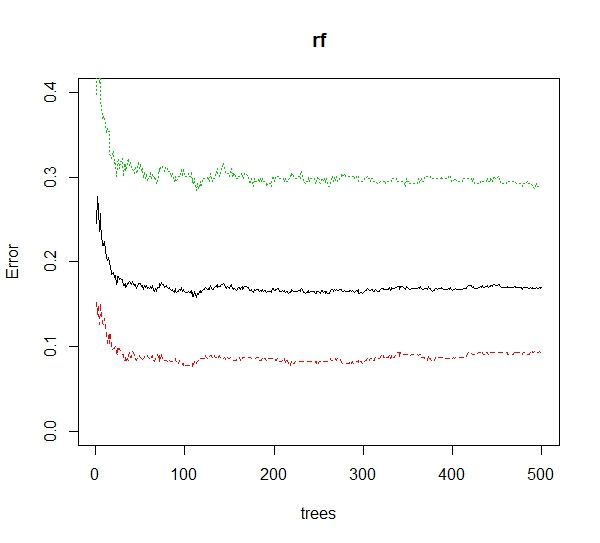
rf = randomForest(Survived~Sex+Age+Pclass+SibSp+Parch+Fare+Embarked,data = train)
plot(rf,ylim = c(0,0.4))

根据图中可以看到，当决策树数目达到100左右时误差趋于稳定，故选择决策树数量为100.

 rf = randomForest(Survived~Sex+Age+Pclass+SibSp+Parch+Fare+Embarked,data = train,ntree = 100)

提取自变量重要程度

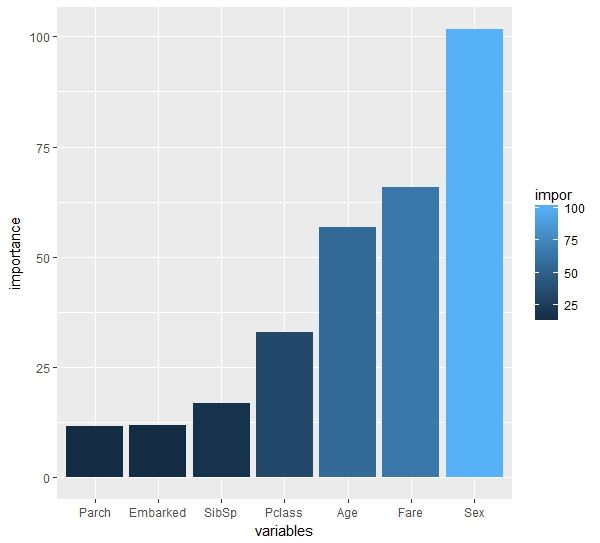
importance = importance(rf)

 

可以看到性别最重要，其次是票价，重要度最低的是父母子女数。

 

对测试集进行预测并写入结果

prediction = predict(object = rf,newdata = test)
result = data.frame(test$PassengerId,prediction)
write.csv(result,file = "rf_result",row.names = F)

个人总结

看了kaggle上的一些大神的分析，发现names可以提取出称号进行分析，考虑到在实际工作过程中此等技巧并不适用，主要通过此次分析过程练习数据分析过程及基本方法等。