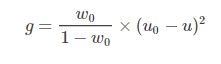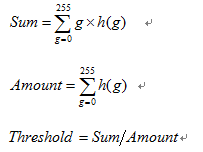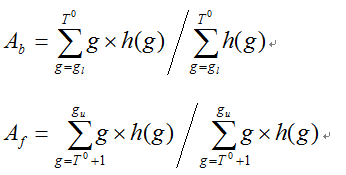图像处理二之----摄像头二值化算法汇总+代码
上一节中我们讲解了什么是二值化,并且讲到了二值化的一般方法,那么每种算法究竟是怎么样对图像经行二值化处理的呢?,算法的原理是什么呢,怎么样用代码实现,这节我们分享下。
1.otsu(最大类间方差法、大津法)
最大类间方差法是由日本学者大津于1979年提出的,是一种自适应的阈值确定的方法,又叫大津法,简称OTSU。它是按图像的灰度特性,将图像分成背景和目标2部分。背景和目标之间的类间方差越大,说明构成图像的2部分的差别越大,当部分目标错分为背景或部分背景错分为目标都会导致2部分差别变小。因此,使类间方差最大的分割意味着错分概率最小。
阈值将原图象分成前景,背景两个图象。
当取最佳阈值时,背景应该与前景差别最大,关键在于如何选择衡量差别的标准
而在otsu算法中这个衡量差别的标准就是最大类间方差(英文简称otsu,这也就是这个算法名字的来源)
对于图像I(x,y),前景(即目标)和背景的分割阈值记作T,前景图像占整幅图像的比例记为ω0,其平均灰度μ0;背景图像占整幅图像的比例为ω1,其平均灰度为μ1。图像的总平均灰度记为μ,类间方差记为g。M×N = 像素总数,图像中像素的灰度值小于阈值T的像素个数记作N0,像素灰度大于阈值T的像素个数记作N1
,则有:
前景图像占比 ω0=N0/ M×N (1)
背景图像占比 ω1=N1/ M×N (2)
前景像素+背景像素 N0+N1=M×N (3)
背景图像+前景图像占比 ω0+ω1=1 (4)
0~M灰度区间的灰度累计值 ![]() (5)
(5)
类间方差值 ![]() (6)
(6)
将式(5)代入式(6),得到等价公式:
![]() (7)
(7)
或
采用遍历的方法得到使类间方差最大的阈值T,即为所求。
代码实现:
c代码
w0为背景像素点占整幅图像的比例
u0为w0平均灰度
w1为前景像素点占整幅图像的比例
u1为w1平均灰度
u为整幅图像的平均灰度
类间方差公式 g = w1 * w2 * (u1 - u2) ^ 2
int otsuThreshold(int *image, int col, int row)
{
#define GrayScale 256
int width = col;
int height = row;
int pixelCount[GrayScale] = {0}; //每个灰度值所占像素个数
float pixelPro[GrayScale] = {0};//每个灰度值所占总像素比例
int i, j, pixelSum = width * height; //总像素
int threshold = 0;
int* data = image; //指向像素数据的指针
//统计灰度级中每个像素在整幅图像中的个数
for (i = 0; i < height; i++)
{
for (j = 0; j < width; j++)
{
pixelCount[(int)data[i * width + j]]++; //将像素值作为计数数组的下标
}
}
//遍历灰度级[0,255]
float w0, w1, u0tmp, u1tmp, u0, u1, u, deltaTmp, deltaMax = 0;
for (i = 0; i < GrayScale; i++) // i作为阈值
{
w0 = w1 = u0tmp = u1tmp = u0 = u1 = u = deltaTmp = 0;
for (j = 0; j < GrayScale; j++)
{
if (j <= i) //背景部分
{
pixelPro[i] = (float)pixelCount[i] / pixelSum; //计算每个像素在整幅图像中的比例
w0 += pixelPro[j];//背景像素点占整个图像的比例
u0tmp += j * pixelPro[j];
}
else //前景部分
{
pixelPro[i] = (float)pixelCount[i] / pixelSum; //计算每个像素在整幅图像中的比例
w1 += pixelPro[j];//前景像素点占整个图像的比例
u1tmp += j * pixelPro[j];
}
}
u0 = u0tmp / w0;//背景平均灰度μ0
u1 = u1tmp / w1;//前景平均灰度μ1
deltaTmp = (float)(w0 *w1* pow((u0 - u1), 2)); //类间方差公式 g = w1 * w2 * (u1 - u2) ^ 2
if (deltaTmp > deltaMax)
{
deltaMax = deltaTmp;
threshold = i;
}
}
return threshold;
}MATALB代码:
close all;
clear all;
clc;
input = imread('R.png');%读图
input = rgb2gray(input);%灰度转换
L = 256;%给定灰度级
[ni, li] = imhist(input,L); %ni-各灰度等级出现的次数;li-对应的各灰度等级
% figure,plot(xi,ni);%显示绝对直方图统计
% title('绝对直方图统计')
[M,N] = size(input);%获取图像大小
MN = M*N;%像素点总数
%%Step1 计算归一化直方图
pi = ni/MN; %pi-统计各灰度级出现的概率
figure,plot(li,pi);%显示相对直方图统计
title('相对直方图统计')
%%Step2 计算像素被分到C1中的概率P1(k)
sum = 0;%用来存储各灰度级概率和
P1 = zeros(L,1);%用来存储累积概率和
for k = 1:L
sum = sum +pi(k,1);
P1(k,1) = sum;%累加概率
end
%%Step3 计算像素至K级的累积均值m(k)
sum1 = 0;%用来存储灰度均值
m = zeros(L,1);%用来存储累计均值
for k = 1:L
sum1 = sum1+k*pi(k,1);
m(k,1) = sum1;%累积均值
end
%%Step4 计算全局灰度均值mg
mg = sum1;
%%Step5 计算类间方差sigmaB2
sigmaB2 = zeros(L,1);
for k = 1:L
if(P1(k,1) == 0)
sigmaB2(k,1) = 0; %为了防止出现NaN
else
sigmaB2(k,1) = ((mg*P1(k,1)-m(k,1))^2)/(P1(k,1)*(1-P1(k,1)));
end
end
%%Step6 得到最大类间方差以及阈值
[MsigmaB2,T] = max(sigmaB2);%获取最大类间方差MsigmaB2,以及所在位置(即阈值)
output = zeros(M,N);%定义二值化输出图像
for i = 1:M
for j = 1:N
if input(i,j)>T
output(i,j) = 1;
else
output(i,j)=0;
end
end
end
figure,imshow(output);%显示结果
%%Step7 可分性度量eta
sigmaG2 = 0;%全局方差
for k = 1:L
sigmaG2 = sigmaG2+(k-mg)^2*pi(k,1);
end
eta = MsigmaB2/sigmaG2;
或者直接调用MATALB函数
I=imread('D:\Images\pic_loc\1870405130305041503.jpg');
a=rgb2gray(I);
level = graythresh(a);
a=im2bw(a,level);
imshow(a,[]);缺陷:OSTU算法在处理光照不均匀的图像的时候,效果会明显不好,因为利用的是全局像素信息。
2.灰度平局值法:
1、描述:即使用整幅图像的灰度平均值作为二值化的阈值,一般该方法可作为其他方法的初始猜想值。
原理:
代码实现:
public static int GetMeanThreshold(int* HistGram)
{
int Sum = 0, Amount = 0;
for (int Y = 0; Y < 256; Y++)
{
Amount += HistGram[Y];
Sum += Y * HistGram[Y];
}
return Sum / Amount;
}缺点:同样受光线影响较大,但是方法简单,处理快
3.双峰法
介绍:如果图像灰度直方图呈明显的双峰状,则选取双峰间的最低谷出作为图像分割的阈值所在。,如下图,以T为阈值进行二值化分,可以将目标和背景分割开。
在一些简单的图像中,物体的灰度分布比较有规律,背景与各个目标在图像的直方图各自形成一个波峰,即区域与波峰一一对应,每两个波峰之间形成一个波谷。那么,选择双峰之间的波谷所代表的灰度值T作为阈值,即可实现两个区域的分割。如下图所示。
代码实现:
int GetIntermodesThreshold(int* HistGram)
{
int Y, Iter = 0, Index;
double* HistGramC = new double[256]; // 基于精度问题,一定要用浮点数来处理,否则得不到正确的结果
double* HistGramCC = new double[256]; // 求均值的过程会破坏前面的数据,因此需要两份数据
for (Y = 0; Y < 256; Y++)
{
HistGramC[Y] = HistGram[Y];
HistGramCC[Y] = HistGram[Y];
}
// 通过三点求均值来平滑直方图
while (IsDimodal(HistGramCC) == false) // 判断是否已经是双峰的图像了
{
HistGramCC[0] = (HistGramC[0] + HistGramC[0] + HistGramC[1]) / 3; // 第一点
for (Y = 1; Y < 255; Y++)
HistGramCC[Y] = (HistGramC[Y - 1] + HistGramC[Y] + HistGramC[Y + 1]) / 3; // 中间的点
HistGramCC[255] = (HistGramC[254] + HistGramC[255] + HistGramC[255]) / 3; // 最后一点
memcpy(HistGramCC, HistGramC, 256 * sizeof(double)); // 备份数据,为下一次迭代做准备
Iter++;
if (Iter >= 10000) return -1; // 似乎直方图无法平滑为双峰的,返回错误代码
}
// 阈值为两峰值的平均值
int* Peak = new int[2];
for (Y = 1, Index = 0; Y < 255; Y++)
if (HistGramCC[Y - 1] < HistGramCC[Y] && HistGramCC[Y + 1] < HistGramCC[Y]) Peak[Index++] = Y - 1;
return ((Peak[0] + Peak[1]) / 2);
}
bool IsDimodal(double* HistGram) // 检测直方图是否为双峰的
{
// 对直方图的峰进行计数,只有峰数位2才为双峰
int Count = 0;
for (int Y = 1; Y < 255; Y++)
{
if (HistGram[Y - 1] < HistGram[Y] && HistGram[Y + 1] < HistGram[Y])
{
Count++;
if (Count > 2) return false;
}
}
if (Count == 2)
return true;
else
return false;
}Python代码:
#coding:utf-8
import cv2
import numpy as np
from matplotlib import pyplot as plt
image = cv2.imread("E:/python/cv/2ModeMethod/test.jpg")
gray = cv2.cvtColor(image, cv2.COLOR_BGR2GRAY)
plt.subplot(131), plt.imshow(image, "gray")
plt.title("source image"), plt.xticks([]), plt.yticks([])
plt.subplot(132), plt.hist(image.ravel(), 256)
plt.title("Histogram"), plt.xticks([]), plt.yticks([])
ret1, th1 = cv2.threshold(gray, 127, 255, cv2.THRESH_BINARY)
plt.subplot(133), plt.imshow(th1, "gray")
plt.title("2-Mode Method"), plt.xticks([]), plt.yticks([])
plt.show()
缺点:当不同区域(即目标)之间的灰度分布有一定的重叠时,双峰法的效果就很差,也就是说,图像为双峰时才能用双峰法
上述代码已经给出判断双峰图的代码
4最佳迭代法
迭代法图像二值化的算法思想是:首先,初始化一个阈值Th,然后按照某种策略通过迭代不断更新这一阈值,直到满足给定的约束条件为止。
迭代法是基于逼近的思想,迭代阈值的获取步骤可以归纳如下:
(1)求出图象的最大灰度值和最小灰度值,分别记为gl和gu,令初始阈值为:
(2) 根据阈值T0将图象分割为前景和背景,分别求出两者的平均灰度值Ab和Af:
(3) 令
如果Tk=Tk+1,则取Tk为所求得的阈值,否则,转2继续迭代
MATALB代码实现:
>> clear all
%读入图像
I=imread('D:\Administrator\My Pictures\Lenagray.bmp');
%计算灰度的最小值和最大值
tmin=min(I(:));
tmax=max(I(:));
%设定初始阈值
th=(tmin+tmax)/2;
%定义开关变量,用于控制循环次数
ok=true;
%迭代法计算阈值
while ok
g1=I>=th;
g2=I<=th;
u1=mean(I(g1));
u2=mean(I(g2));
thnew=(u1+u2)/2;
%设定两次阈值的比较,当满足小于1时,停止循环
ok=abs(th-thnew)>=1;
th=thnew;
end
th=abs(floor(th));
%阈值分割
J=im2bw(I,th/255);
%结果显示
figure(1);
imshow(I);title('原始图像');
figure(2);
str=['迭代分割:阈值Th=',num2str(th)];
imshow(J);
title(str);
代码实现:
public static int GetIterativeBestThreshold(int[] HistGram)
{
int X, Iter = 0;
int MeanValueOne, MeanValueTwo, SumOne, SumTwo, SumIntegralOne, SumIntegralTwo;
int MinValue, MaxValue;
int Threshold, NewThreshold;
for (MinValue = 0; MinValue < 256 && HistGram[MinValue] == 0; MinValue++) ;
for (MaxValue = 255; MaxValue > MinValue && HistGram[MinValue] == 0; MaxValue--) ;
if (MaxValue == MinValue) return MaxValue; // 图像中只有一个颜色
if (MinValue + 1 == MaxValue) return MinValue; // 图像中只有二个颜色
Threshold = MinValue;
NewThreshold = (MaxValue + MinValue) >> 1;
while (Threshold != NewThreshold) // 当前后两次迭代的获得阈值相同时,结束迭代
{
SumOne = 0; SumIntegralOne = 0;
SumTwo = 0; SumIntegralTwo = 0;
Threshold = NewThreshold;
for (X = MinValue; X <= Threshold; X++) //根据阈值将图像分割成目标和背景两部分,求出两部分的平均灰度值
{
SumIntegralOne += HistGram[X] * X;
SumOne += HistGram[X];
}
MeanValueOne = SumIntegralOne / SumOne;
for (X = Threshold + 1; X <= MaxValue; X++)
{
SumIntegralTwo += HistGram[X] * X;
SumTwo += HistGram[X];
}
MeanValueTwo = SumIntegralTwo / SumTwo;
NewThreshold = (MeanValueOne + MeanValueTwo) >> 1; //求出新的阈值
Iter++;
if (Iter >= 1000) return -1;
}
return Threshold;
}5百分比阈值(P-Tile法)
p-tile算法是一种基于灰度直方图统计的的自动阈值选择算法,该算法需要基于一定的先验条件—背景与目标所占的面积比P%。
该算法选择阈值的原则是,依次累积灰度直方图,直到该累积值大于或等于前景图像(目标)所占面积,此时的灰度级即为所求的阈值
代码实现:
//HistGram灰度图像的直方图
//Tile背景在图像中所占的面积百分比
int GetPTileThreshold(int* HistGram, int Tile)
{
int Y, Amount = 0, Sum = 0;
for (Y = 0; Y < 256; Y++) Amount += HistGram[Y]; // 像素总数
for (Y = 0; Y < 256; Y++)
{
Sum = Sum + HistGram[Y];
if (Sum >= Amount * Tile / 100) return Y;
}
return -1;
}
缺点:该方法简单高效,但是对于先验概率难于估计的图像却无能为力。。条件很苛刻,大部分情况下都用不上
6.Niblack二值化算法
Niblack二值化算法是比较简单的局部阈值方法,阈值的计算公式是T = m + k*v,其中m为以该像素点为中心的区域的平均灰度值,v是该区域的标准差,k是一个修正系数
它根据以像素点为中心的邻域内的点的情况为此像素计算阈值。下面是每个像素阈值的计算公式,m是均值,s是标准差
MATALB代码:
function g=segNiBlack(f,w2,k)
% segmentation method using Niblack thresholding method
% input: w2 is the half width of the window
w = 2*w2 + 1;
window = ones(w, w);
% compute sum of pixels in WxW window
sp = conv2(f, window, 'same');
% convert to mean
n = w^2; % number of pixels in window
m = sp / n;
% compute the std
if k ~= 0
% compute sum of pixels squared in WxW window
sp2 = conv2(f.^2, window, 'same');
% convert to std
var = (n*sp2 - sp.^2) / n / (n-1);
s = sqrt(var);
% compute Niblack threshold
t = m + k * s;
else
t = m;
end
g=fC代码:
void NiBlack(BYTE *image_in, BYTE *image_out, int xsize, int ysize)
{
/*
// 作者:杨魁
//参数列表:
//image_in 输入图像的指针
//image_out 输出图像的指针
//xsize 图像的宽
//ysize 图像的高
*/
int sum = 0;
int i, j, h, k;;//用于循环
int Average = 0;//平均值
int num = 0;//用于自加
int w_size = 7;//窗口大小为2*w_size+1
int Area = (2 * w_size + 1)*(2 * w_size + 1);
int *d = (int *)malloc(sizeof(int)*Area);//数组空间
int T = 0;//阈值
int S = 0;//标准差
for (j = w_size; j < ysize - w_size; j++)
{
for (i = w_size; i < xsize - w_size; i++)
{
sum = 0;
num = 0;
for (h = 0; h < 2 * w_size + 1; h++)
{
for (k = 0; k < 2 * w_size + 1; k++)
{
d[num++] = GetGray(image_in, xsize, i + w_size - k, j + w_size - h); //求area领域内的像素值
}
}
for (h = 0; h T ? 255 : 0;
}
}
free(d);
C#
///
/// 快速的二维数组元素局部窗口求和程序
///
/// 输入二维数组
/// 窗口半径
/// 输出结果
///
public static int[,] LocalSum_Fast(byte[,] array, int winR)
{
int width = array.GetLength(0);
int height = array.GetLength(1);
int[,] temp = new int[width, height];//保存中间结果的数组
int[,] sum = new int[width, height];
//不考虑边界情况,
//水平方向:winR行至width-winR行,
//垂直方向:winR列至width-winR列
//对起始行winR在垂直方向求线性和
for (int x = winR; x < width - winR; x++)
{
for (int k = -winR; k <= winR ; k++)
{
temp[x, winR] += array[x, winR + k];
}
}
//从winR+1行至末尾行height-winR,依次基于前一行的求和结果进行计算。
for (int y = winR + 1; y < height - winR; y++)
{
for (int x = winR; x < width - winR; x++)
{
temp[x, y] = temp[x, y - 1] + array[x, y + winR]
- array[x, y - 1 - winR];
}
}
//基于保存的垂直方向求和结果,进行水平方向求和
//对起始列winR在水平方向求线性和
for (int y = winR; y < height - winR; y++)
{
for (int k = -winR; k <= winR ; k++)
{
sum[winR, y] += temp[winR + k, y];
}
}
//从winR+1列至末尾列height-winR,依次基于前一列的求和结果进行计算。
for (int x = winR + 1; x < width - winR; x++)
{
for (int y = winR; y < height - winR; y++)
{
sum[x, y] = sum[x - 1, y] + temp[x + winR, y]
- temp[x - winR - 1, y];
}
}
//运算完成,输出求和结果。
return sum;
}
7.bernsen二值化
bernsen算法的中心思想:
先人为设定两个值S与TT(Bemsen最初设S为15,TT设为128),计算以图像中任意像素尸为中心的大小为k×k窗口内的所有像素的最大值M与最小值N,两者的均值T,如果朋M-N大于S,则当前P的阈值为T;若小于S,则表示该窗口所在区域灰度级灰度级差别较小,那么窗口在目标区或在背景区,再判断T与TT的关系,若T>TT则当前点灰度值为255,否则当前点灰度值为0。
改进的bernsen算法:
1.消除个别灰度特异点,设采用的阈值为T1。
A为图像的总像素个数
代码实现:
int getThreshBernsen(IplImage *src)
{
uchar num[256];
int w = src->width;
int h = src->height;
int s = src->widthStep;
int T1 = 0;
int pix = 0;
int a = w * h;
memset(num, 0, 256);
//统计灰度值的个数
for(int i=0; i<=255; i++)
{
for(int j=1; j<= h; j++)
{
for(int m=1; m<= w; m++)
{
if(((uchar*)src->imageData + j*s)[m] == i)
{
num[i] = num[i] + 1;
}
}
}
}
for(int i=255; i>=0; i--)
{
pix = pix + num[i];
if(pix >= (0.1*a))
{
T1 = i;
break;
}
}
cout << T1 << endl;
return T1;
}
二值化的方法有很多,基于每个人来说都会有着适合自己的方法,这里我们只介绍上述几种主流方法,正常使用已经足以,方法不在于多,而在于精,可能你用一种方法就很完美,也可能要不断修改,找到最适合的,图像处理好才是王道。
参考:
ttps://www.cnblogs.com/Imageshop/p/3307308.html
https://blog.csdn.net/liuzhuomei0911/article/details/51440305
https://blog.csdn.net/jinzhichaoshuiping/article/details/51480520
https://www.cnblogs.com/naniJser/archive/2012/12/12/2814324.html
https://blog.csdn.net/wu_lian_nan/article/details/69371720
https://blog.csdn.net/zyzhangyue/article/details/45841121
还有一些参考较少的文献,这里就不罗列了,写这个用到参考文献实在太多,抱歉抱歉
整理实属不易,点个赞再走呗!