快乐地打牢基础（4）——树状数组

在解题的过程中，我们想维护一个数组的前缀和s[i] = A[1] + A[2] +…+A[i]。我们改变任意一个A[i],那么S[i]之后都会发生变化，朴素写法调整前缀和S最坏的情况需要O(n)的时间。所以引入树状数组，它的修改和求和都是O(logn)的，效率非常高。

一、基本思想

---

根据任意正整数关于2的不重复次幂的唯一分解性质，若一个正整数x的二进制表示为10101，其中等于1 的位置是0，2，4，那么正整数x可以被“二进制分解”成2 ^ 4 + 2 ^ 2 + 2^0。区间[1,x]可以被分成O(logx)个小区间。
长度为2 ^ 4的小区间[1,2 ^ 4]。
长度为2 ^ 2的小区间[2 ^ 4+1,2 ^ 4+2 ^ 2]。
长度为2 ^ 0的小区间[2 ^ 4+2 ^ 2 + 2,2 ^ 4+2 ^ 2 + 2 ^ 0]。

对于给定序列A，我们建立一个数组从，其中c[x]保存序列A的区间[x-lowbit(x)+1,x]中所有的和。
形成下图的树形结构：

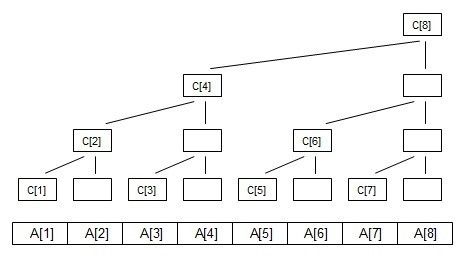
从图中可以得到C[]和A[]关系：C[i]=A[i-2^ k+1]+A[i-2^k+2]+…A[i]; （k为i的二进制中末尾0的数量）
该结构满足一下的性质：

• 1.每个内部结点C[x]保存以它为根的子树中所有叶结点的和。
• 2.每个内部结点C[x]的子节点个数等于lowbit(x)的位数。
• 3.除树根外，每个内部节点C[x]的父结点是C[x + lowbit(x)].
• 4.树的深度为O（logN）。

二、算法操作

---

由于之前已经整理过树状数组原理的博客：https://blog.csdn.net/sinat_40872274/article/details/97895705
所以直接给出重要操作。
例如i=8时，k=3;

1.求lowbit（x）

lowbit（x）表示取出x的最低位1 换言之 lowbit(x)=2^k （ k为k为x的二进制中末尾0的数量）。
lowbit(x) = x&(-x)是怎么来的呢？具体分析一下

设x > 0,x的第k位上是最低位的1，后边还有若干个0。
先把x取反，此时第k位变成0，第0~到k-1位都是1。
再令x = x +1,此时因为进位，第k位变成1，第0~k-1位都是0.在上面的取反加1的 操作后，x的第k+1位到最高位因为取反，所以是与原来相反的，这样一来x&（ ~ x+1）运算过后就只有第k位上是1了。而补码 ~x = -x-1 ,因此lowbit（x） = x&（-x）。
代码：

int lowbit(int x){
	return x&-x;
}

2.对某个元素进行加法操作

树状数组支持单点增加，意思是给序列中的某个数A[x]加上y，同时正确维护序列的前缀和，根据上面给出的树形结构和它的性质，只有结点C[x]及其所有祖先你结点保存的“区间和”包含结点A[x]，而任意一个结点的祖先至多只有logN个，所以逐一对包含A[x]的C[]值进行更新就可以了,这样可以在O(logN)时间内执行单点增加操作。
那么我们的现在就是要解决如和找到A[x]的祖先结点。这就要回顾这个树形结构的第三点性质了。

• 3.除树根外，每个内部节点C[x]的父结点是C[x + lowbit(x)]。

代码：

void update(int x,int y){
	for(;x<= N; x += lowbit(x)) c[x] += y;
	return ans;
}

3.查询前缀和

树状数组支持查询前缀和，即序列A第1~x个数的和。按照我们刚才提出的方法，应该求出x的二进制表示中每个等于1的位，把[1,x]分成O（logN）个小区间，而每个小区间的和都已经存在数组C[]中了，所以直接求代表每个小区间的C[]的和就行了。

int sum(int x){
	int ans = 0;
	for(; x; x -= lowbit(x)) ans += c[x];
	return ans;
	//可以发现求前缀和与加法操作 是两个逆序的过程
}

4.统计A[x]…A[y]的值

前缀和思想：sum(y) - sum(x-1)

5.多维树状数组

将一维的树状数组变成m维的，那么时间复杂度就是O((logN)^m)，在m不大的时候，还是可以接受的。扩充的方法就是将原来的修改和查询函数中的一个循环，改成m个循环m维数组c中的操作。下面以n*m的二维数组a，树状数组c为例，给出单点增加和求和操作的代码。

//单点增加
void update(int x,int y ,int z){//将（x,y）的值加上z
	int i = x;
	while(i <= n){
		int j = y;
		while(j <= m){
			c[i][j] += z;
			j += lowbit(j);
		}
		i += lowbit(i);
	}
}
//求前缀和
int sum(int x,int y){
	int ans = 0,i = x;
	while(i > 0){
		int j = y;
		while(j > 0){
			ans += c[i][j];
			j -= lowbit(j);
		}
		i -= lowbit(i);
	}
	return ans;
}

6.注意事项

树状数组可以处理的是下标从1开始的数组，不能出现下标为0的情况，因为lowbit(0) = 0，会导致死循环。

【例题1】 一本通 OJ 1535：数列操作
题意
给定一个有n个数的数列,规定有两种操作，一是修改某个元素，二是求子数列[a,b]的连续和。数列元素个数最多10万个，询问操作最多10万次。
思路
定义模板题，由于查询次数大，所以树状数组相较于线段树更好一些。

#include 

using namespace std;
const int Max = 1e6 + 10;
int n,m;
int a[Max] = {0},c[Max] = {0}; 
int lowbit(int x){
	return x&(-x);
}
void update(int x,int y){
	for(; x <= n; x += lowbit(x)) c[x] += y; 
}
int sum(int x){
	int ans  = 0;
	for(; x; x -= lowbit(x)) ans += c[x];
	return ans;
}
int main(){
	scanf("%d %d",&n,&m);
	for(int i = 1; i<= n; i++) {
		scanf("%d",&a[i]);
		update(i,a[i]);
	}
	int k,x,y;
	while(m--){
		scanf("%d %d %d",&k,&x,&y);
		if(k == 0){
			printf("%d\n",sum(y) - sum(x-1));
		}else{
			update(x,y);
		}
	}
	return 0;
} 

【例题2】 一本通OJ 1536：数星星 Stars （Ural 1028 ）
题意
给出n个点的坐标，找出这n个点的左边，下边和左下共有几个点。
思路
看到二维坐标，感觉像是二维的树状数组，但由于点是按y从小到大给出的，所以我们只考虑点的x坐标就可以，只要在第i点前给出的点的x 小于等于i点的x，那么这个点就是合法的。

设a[i]为横坐标x为i-1的点的个数，要是找第k个点的合法点有多少，那么就是a[1]…a[k+1]的和，因为我们使用树状数组下标是不可以从0开始的，但是点的x坐标是从0开始的，所以采用这种x+1的方法。

#include 
using namespace std;

const int Max = 33000;
int a[Max],c[Max],cnt_star[Max],xi[Max],yi[Max];
int n;
int lowbit(int x){
	return x&-x;
}
void update(int x,int y){
	for(; x <= Max; x += lowbit(x)) c[x] += y;
}
int sum(int x){
	int ans = 0;
	for(; x; x -= lowbit(x)) ans += c[x] ;
	return ans; 
}
int main(){
	scanf("%d",&n);
	for(int i = 1; i <= n; i++){
		scanf("%d %d",&xi[i],&yi[i]);
	}
	for(int i = 1; i <= n; i++){
		int res = sum(xi[i]+1);
		update(xi[i]+1,1);
		cnt_star[res]++;
	}
	for(int i = 0; i < n; i++)
		printf("%d\n",cnt_star[i]);
	
}

【例题3】1537 校门外的树（Vijos P1448）
题意
学校在某个时刻在某一段种上一种树，每次种的树种类不同，给出一个区间[l,r]问这个区间里有多少种树。
思路
这个问题的重点应该在找到每次种树时的起点和终点。
一本通书上给了一个有趣的比喻，对于插入的线段[li,ri]把数轴上li处看成一个‘（’表示开始种，ri处看成一个‘）’表示种结束了。
对于询问区间[lq,rq]：
rq左边’（'的个数就表示从开头到rq中树的种类数。
lq左边‘）’的个数就表示有多少种树没有种在询问区间[lq,rq]中，我们因此要减去这些种类。
可以发现，rq左边的‘（’的个数 减去 lq左边‘）’的个数 就是我们需要的答案。仔细想想，就是要求‘（’和‘）’的前缀和，然后相减。

拿样例举个例子：

前缀和 ，区间，对点修改 ，多次查询区间 ，所以想到树状数组。

• 1.建立两个树状数组T1和T2分别维护‘（’和‘）’。
• 2.若k = 1，读入li，ri，updateT1（li，1），updateT2（ri，1）。
• 3.若k = 2，读入lq,rq sumT1（rq） - sumT2（lq-1）。

#include
using namespace std;

const int Max = 5e4 + 10;
int T1[Max],T2[Max];
int n,m;
int lowbit(int x){
	return x & -x;
}
void update(int x,int y,int T[]){
	for(; x <= n; x += lowbit(x)) T[x] += y; 
}
int sum(int x,int T[]){
	int res = 0;
	for(; x; x -= lowbit(x)) res += T[x];
	return res;
}
int main(){
	scanf("%d %d",&n,&m);
	int k,l,r;
	for(int i = 1; i <= m; i++){
		scanf("%d %d %d",&k,&l,&r);
		if(k == 1){
			update(l,1,T1);
			update(r,1,T2); 
		}else{
			int ans = sum(r,T1) - sum(l-1,T2);
			printf("%d\n",ans); 
		}
	}
	
	return 0;
}

练习题：一本通OJ

1538 清点人数
1539 简单题
1540 打鼹鼠_二维树状数组

本文完全照抄 参考黄新军 董永建《信息学奥赛一本通·提高》