动态规划之图形的压缩

目录

1. 图形的压缩简介
2. 详细说明
3. 最优子结构性质
4. 举例
5. 代码块
6. 测试结果

---

图形的压缩简介

在计算机中常用像素点灰度值序列{p1,p2,….,pn}表示图像。其中，整数pi(1<=i<=n)表示像素点i的灰度值。
灰度值的范围是0~255。因此需要用8位表示一个像素。

压缩的原理就是吧序列{p1,p2,……pn}进行设断点，将其分割成一段一段的。分段的过程就是要找出断点，让一段里面的像素的最大灰度值比较小，那么这一段像素(本来需要8位)就可以用较少的位(比如7位)来表示，从而减少存储空间。

---

举例及其详细说明

设置三个数组 b[],l[],s[],b代表bits,l代表length,s代表sum。b[]代表每段一个像素点所需要的最小存储空间。
l[]代表每段有几个像素点。s[]代表从0压缩到i的所有像素点占的最小空间。

如果限制l[i]<=255,则需要8位来表示[i]。而b[i]<=8,需要3位表示b[i],所以每段所需的存储空间位l[i]*b[i]+11位。假设将原图分成m段，那么需要
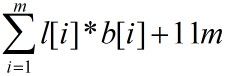位的存储空间

图像压缩问题就是要确定像素序列{p1,p1,……pn}的最优分段，使得依此分段所需的存储空间最小。

---

最优子结构性质

设l[i],b[i],1<=i<=m是{p1,p2…..,pn}的最优分段。显而易见，l[1],b[1]是{p1,….,pl[1]}的最优分段，且l[i],b[i],2<=i<=m是{pl[i]+1,…pn}的最优分段。即图像压缩问题满足最优子结构性质.又因为断点可以在最有分段之间随意选择最后来选择最小的一个压缩空间，所以要求最优分段的min。即：
设s[i],1<=i<=n是像素序列{p1,p1,……pi}的最优分段所需的存储位数，则s[i]为前i-k个的存储位数加上后k个的存储空间。由最优子结构性质可得：

---

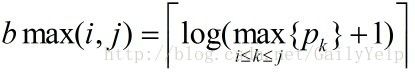
举例

下面展示了像素序列从p1~pn递增过程中，其断开点的i寻找，以及最小的最优压缩空间的寻找。

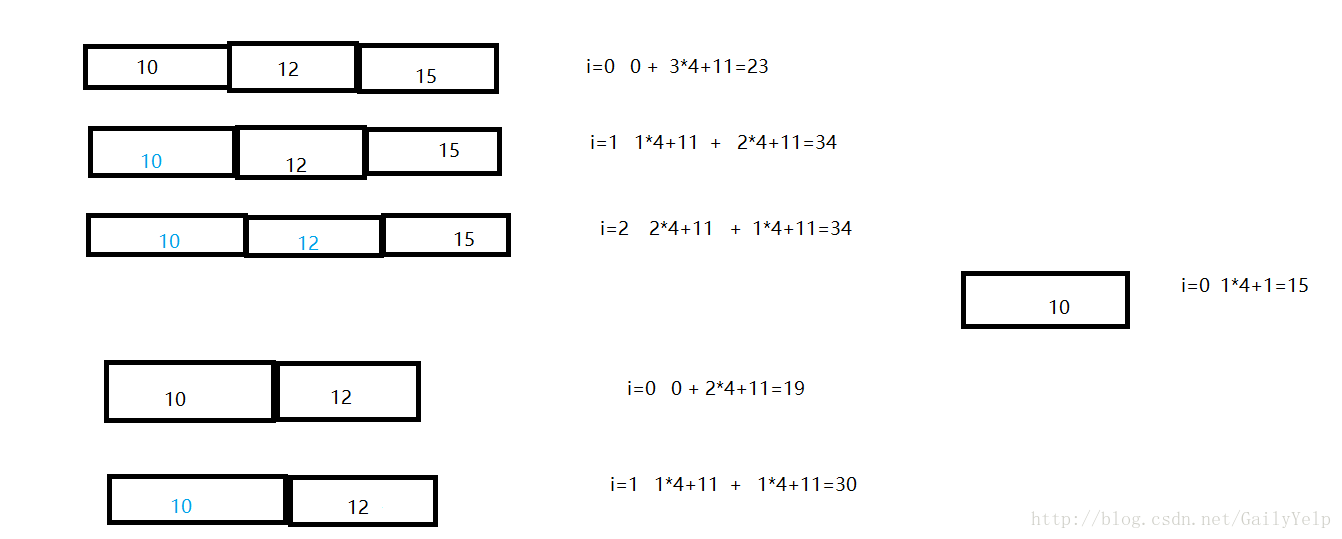
p1时 最小压缩空间为15 b[1]=4 l[1]=1
p2时 最小压缩空间为 19 b[2]=4 l[2]=2
p3时 最小压缩空间为 23 b[3]=4 l[3]=3

p4时 最小压缩空间为 42 b[4]=8 l[4]=1

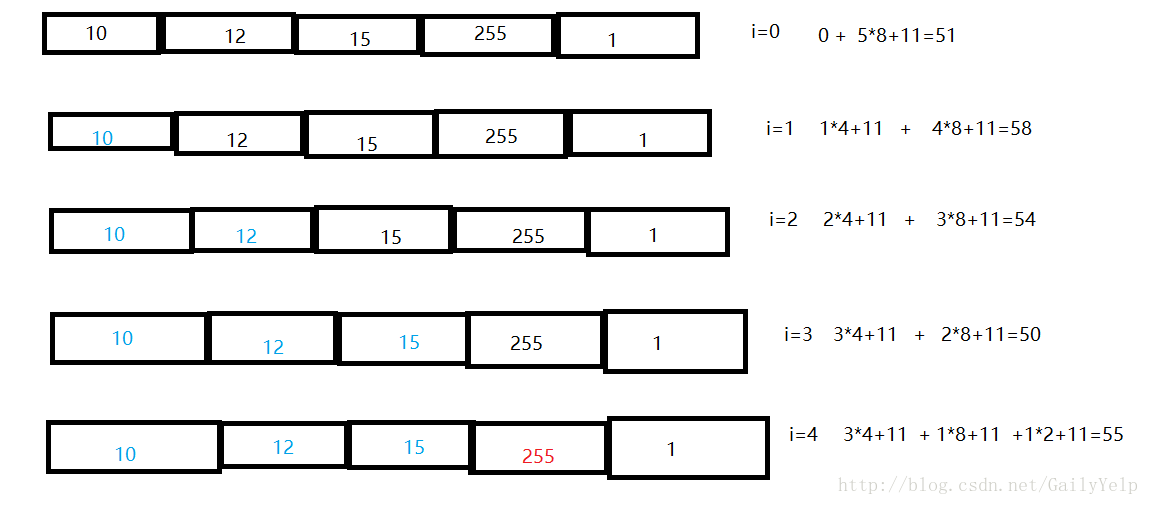
p5时 最小压缩空间为 50 b[5]=8 l[5]=2

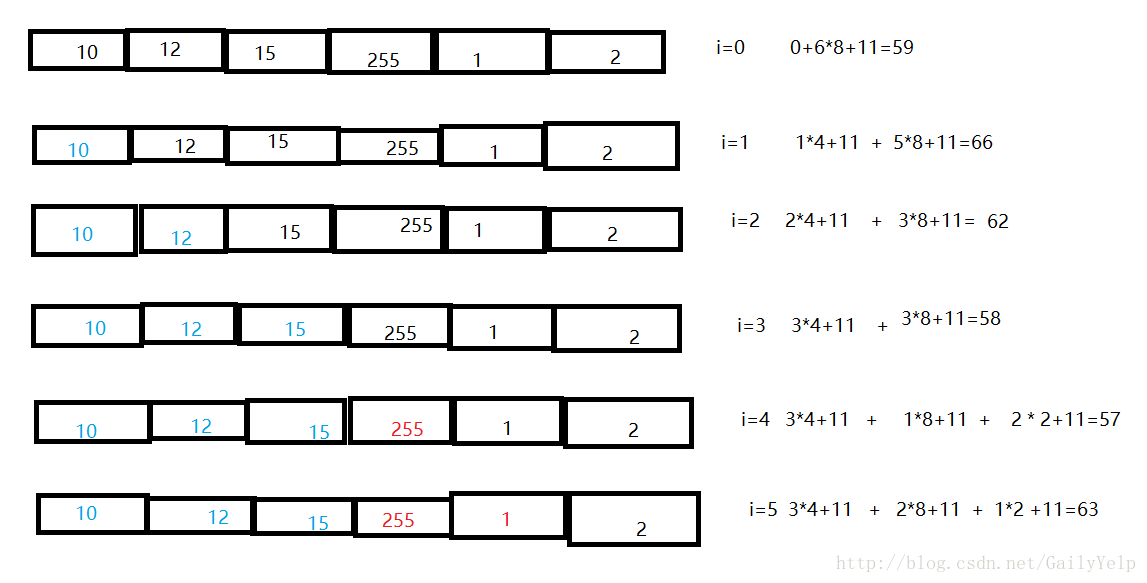
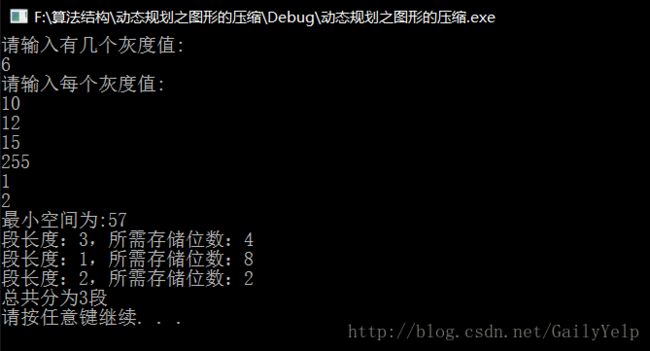
p6时 最小压缩空间为 57 b[6]=2 l[6]=2

因为 2^3<10<2^4 (每个像素点的最少占4位)
2^3<12<2^4 (每个像素点的最少占4位)
2^3<15<2^4 (每个像素点的最少占4位)
2^7<255<2^8 (每个像素点的最少占5位)

---

代码块

#include
#include
#define MAX 20
int seg;

void backtack(int s[], int b[], int l[], int n)
{
    if (n == 0){
        return;
    }
    else {
        seg += 1;
        backtack(s, b, l, n - l[n]);
        printf("段长度：%d，所需存储位数：%d\n",
            l[n], b[n]);
    }
}

int maxbit(int p[], int start, int end)
{
    int bitmax, maxvalue;
    maxvalue = 0;
    int i;
    for (i = start; i < end; i++)
    {
        maxvalue = maxvalue>p[i] ? maxvalue : p[i];
    }
    bitmax = 1;
    i = maxvalue / 2;
    while (i > 0)
    {
        bitmax++;
        i /= 2;
    }
    return  bitmax;
}

void compress(int p[], int b[], int l[], int s[], int n)
{
    int i, k, tmp;
    int bitmax;
    s[0] = 0;//s[0]作为一个中间变量
    s[1] = maxbit(p, 0, 1)+11;//是指前一个分段中每个像素最小存储空间
    l[1] = 0;
    for (i = 2; i <= n; i++)//因为前一个分段已经求出所以从前二个分段开始指导前n个分段
    {
        for (k = 0; k < i; k++)//前i个分段的压缩空间中可以分为0-k分段的压缩空间和k+1到i分段的压缩空间
        {                     //又因为在计算式s[k]已经算出 只需要计算k+1到i的每个像素的最小存储空间*分段个数 
            bitmax = maxbit(p, k, i);               //即s[k]+bitmax*(i-k);而且k有i-k中选择
            tmp = s[k] + bitmax*(i - k) + 11;
            if (s[i]>tmp)
            {
                s[i] = tmp;
                l[i] = i - k;  //表明这个压缩段有几个像素点
                b[i] = bitmax; //表示这个压缩段每个像素点最少占几个位置。
            }
        }
    }
}


int main(void)
{
    int i;
    int n;
    printf("请输入有几个灰度值:\n");
    scanf("%d", &n);
    int *p;
    p = (int *)malloc(n*sizeof(int));
    int b[MAX];
    int l[MAX];
    int s[MAX];//0到i压缩占多少空间
    printf("请输入每个灰度值:\n");
    for (i = 0; i < n; i++)
    {
        scanf("%d", &p[i]);
    }
    for (i = 0; i < MAX; i++)
    {
        s[i] = 999;
    }
    compress(p, b, l, s, 6);

    printf("最小空间为:%d\n", s[6]);
    seg = 0;
    backtack(s, b, l, 6);
    printf("总共分为%d段\n", seg);

    system("pause");
    return 0;

}

---

测试结果