HOG特征提取全Numpy实现
目录
HOG步骤详解
HOG用Numpy代码实现的下载地址
HOG特征实现的主要步骤(代码实现部分,缺少处理block):
代码功能:
代码详解(代码根据我自己的理解修改一部分,主体一样):
1.导入必要库,注意在jupter画图要加%matplotlib inline
2.显示图片->图片灰度化
3.调整图片大小,调整为cell尺寸大小的整数倍,避免后面cell分割的时候剩余
4.gamma校准,为了防止光照亮度干扰->图片gamma校准
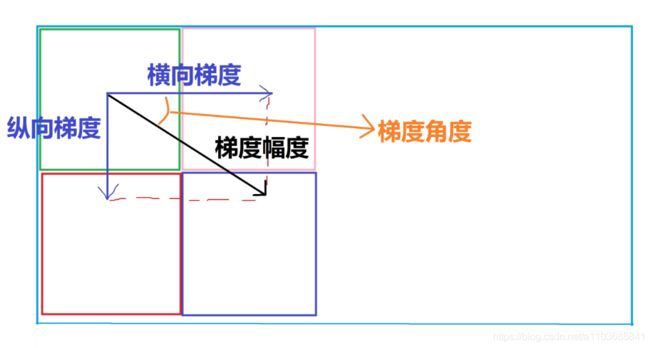
5.得到特征信息->得到图片的横向梯度,纵向梯度,计算图片的梯度和方向
5.1 横向梯度(纵向梯度一致)详解
5.2 计算梯度幅度和方向->计算图片的梯度和方向
6.统计每个cell的特征量->统计cell直方图信息
6.1 创建一个cell(这里刚好我们图片大小就等于我们的cell大小,我这个是特例)
6.2 对cell进行统计->统计cell直方图信息
6.3 显示一下统计量
6.4 cell的物理意义
HOG步骤详解
HOG用Numpy代码实现的原下载地址,我改编的下载地址
HOG特征实现的主要步骤(代码实现部分,缺少处理block):
- 图片gamma矫正
- 得到图片的横向梯度
- 得到图片的纵向梯度
- 得到图片的梯度和方向
- 统计cell直方图信息
代码功能:
HOG_implementation.py:放置提取HOG特征的主要步骤
HOG.py:放置具体实现HOG特征的方法
代码详解(代码根据我自己的理解修改一部分,主体一样):
1.导入必要库,注意在jupter画图要加%matplotlib inline
import cv2
import numpy as np
import matplotlib.pyplot as plt
#解决jupter在结果中显示图片的问题
%matplotlib inline
#解决plt显示中文乱码的问题
plt.rcParams['font.sans-serif']=['SimHei']
plt.rcParams['axes.unicode_minus'] = False
for model in cv2, np:
print(model.__name__,"的版本是:",model.__version__)结果如下:
2.显示图片->图片灰度化
#用灰度模式读取cv2.IMREAD_GRAYSCALE
img = cv2.imread('HOG_stampe1.jpg',cv2.IMREAD_GRAYSCALE)
plt.imshow(img, cmap=plt.cm.gray)
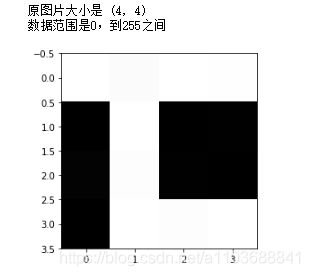
print('原图片大小是',img.shape)
print('数据范围是{},到{}之间'.format(np.min(img),np.max(img)))
plt.show()结果如下:
3.调整图片大小,调整为cell尺寸大小的整数倍,避免后面cell分割的时候剩余
#我这个cell的尺寸设置的比较小是为了,可以更好的显示出来用于理解。
#正常cell的尺寸是8
cell_size = 4
img_w = img.shape[0]//cell_size*cell_size
img_h = img.shape[1]//cell_size*cell_size
#cv2.INTER_CUBIC是一种放大缩小的插值手段
img = cv2.resize(img, (img_h,img_w), interpolation=cv2.INTER_CUBIC)
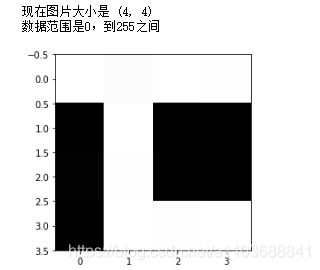
print('现在图片大小是',img.shape)
#数据归一化,让后面有的n次方处理不会超界
img = img/np.max(img)
print('数据范围是{},到{}之间'.format(np.min(img),np.max(img)))
plt.imshow(img, cmap=plt.cm.gray)
plt.show()结果如下:
4.gamma校准,为了防止光照亮度干扰->图片gamma校准
(我下面的代码输入图片数据没有改为gamma校准后的,是因为为了理解图片,我特地做了一个不是纯白就是纯黑的图片,gamma校准后图片的数值就不纯净了,不容易理解。大家到真实图片的时候需要改下面的输入图片)
#做gamma变化前要做数据归一化img/float(np.max(img),防止最后得到数据值太大
#做完归一化后,图片最大为1,1的n次方为1,不会超界
img_gamma = np.power(img/float(np.max(img)), 0.5)
plt.imshow(img_gamma, cmap=plt.cm.gray)
print('伽马矫正后数据范围是{},到{}之间'.format(np.min(img_gamma),np.max(img_gamma)))
plt.show()结果如下:
5.得到特征信息->得到图片的横向梯度,纵向梯度,计算图片的梯度和方向
horizontal_mask = np.array([[-1, 0, 1],
[-1, 0, 1],
[-1, 0, 1]])
vertical_mask = np.array([ [-1, -1, -1],
[0, 0, 0],
[1, 1, 1]])
vDim = horizontal_mask .size
hDim = vertical_mask .size
print('横向梯度算子维度是{},纵向是{}'.format(vDim,hDim))
horizontal_gradient = calculate_gradient(img, horizontal_mask)
vertical_gradient = calculate_gradient(img, vertical_mask)
grad_magnitude = gradient_magnitude(horizontal_gradient, vertical_gradient)
grad_direction = gradient_direction(horizontal_gradient, vertical_gradient)
plt.figure()
plt.subplot(2,2,1)
plt.title('横向梯度')
plt.imshow(horizontal_gradient, cmap=plt.cm.gray)
plt.subplot(2,2,2)
plt.title('纵向梯度')
plt.imshow(vertical_gradient, cmap=plt.cm.gray)
plt.subplot(2,2,3)
plt.title('总梯度')
plt.imshow(grad_magnitude, cmap=plt.cm.gray)
plt.subplot(2,2,4)
plt.title('梯度方向')
plt.imshow(grad_direction, cmap=plt.cm.gray)
plt.show()结果如下:
5.1 横向梯度(纵向梯度一致)详解
5.1.1 预准备工作
plt.figure()
plt.subplot(2,2,1)
plt.title('原图是')
plt.imshow(img,cmap=plt.cm.gray)
#建立sobel的边缘算子,分别是横向和纵向
horizontal_mask = np.array([[-1, 0, 1],
[-1, 0, 1],
[-1, 0, 1]])
vertical_mask = np.array([ [-1, -1, -1],
[0, 0, 0],
[1, 1, 1]])
ts = horizontal_mask.shape[0]
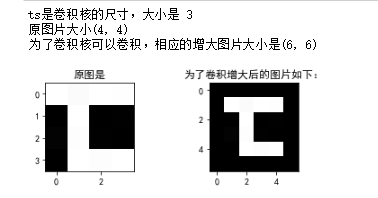
print('ts是卷积核的尺寸,大小是',ts)
new_img = np.zeros((img.shape[0]+ts-1,img.shape[1]+ts-1))
print('原图片大小{}\n为了卷积核可以卷积,相应的增大图片大小是{}'.format(img.shape,new_img.shape))
new_img[np.uint16((ts-1)/2.0):img.shape[0]+np.uint16((ts-1)/2.0),
np.uint16((ts-1)/2.0):img.shape[1]+np.uint16((ts-1)/2.0)] = img
#result用于存放最后得到的边缘梯度数值
result = np.zeros((new_img.shape))
plt.subplot(2,2,2)
plt.title('为了卷积增大后的图片如下:')
plt.imshow(new_img,cmap=plt.cm.gray)
plt.show()结果如下:
5.1.2 提取的卷积显示
plt.figure(figsize=(15,15))
#这里的r和c是根据卷积大小,在为了卷积放大后的特征图上定位原图的大小,或者说卷积核中心的卷积的位置范围
for r in np.uint16(np.arange((ts-1)/2.0, img.shape[0]+(ts-1)/2.0)):
for c in np.uint16(np.arange((ts-1)/2.0,img.shape[1]+(ts-1)/2.0)):
#根据卷积核的中心点,提取出要卷积的图像
curr_region = new_img[r-np.uint16((ts-1)/2.0):r+np.uint16((ts-1)/2.0)+1,
c-np.uint16((ts-1)/2.0):c+np.uint16((ts-1)/2.0)+1]
#进行卷积操作
curr_result = curr_region * horizontal_mask
score = np.sum(curr_result)
#对应赋值(这边为什么不选用和原图一样的大小存放卷积值,反而选一个为了卷积而扩大的矩阵呢?)
#这边仅仅是为了下面赋值时候,不用在计算对应回原图的映射关系了,仅此而已
result[r, c] = score
plt.subplot(img.shape[0]*2+2, img.shape[1],(r-1)*4+(c))
plt.imshow(curr_region, cmap=plt.cm.gray)
plt.subplot(img.shape[0]*2+2, img.shape[1], img.size+(r-1)*4+(c))
plt.imshow(curr_result, cmap=plt.cm.gray)
result_img = result[np.uint16((ts-1)/2.0):result.shape[0]-np.uint16((ts-1)/2.0),\
np.uint16((ts-1)/2.0):result.shape[1]-np.uint16((ts-1)/2.0)]
horizontal_gradient = result_img
plt.subplot(img.shape[0]*2+2,1, img.shape[0]*2+1)
plt.title('卷积后的:')
plt.imshow(result, cmap=plt.cm.gray)
plt.subplot(img.shape[0]*2+2,1, img.shape[0]*2+2)
plt.title('裁剪后还原')
plt.imshow(result_img, cmap=plt.cm.gray)
plt.tight_layout()
plt.show()结果如下:
5.2 计算梯度幅度和方向->计算图片的梯度和方向
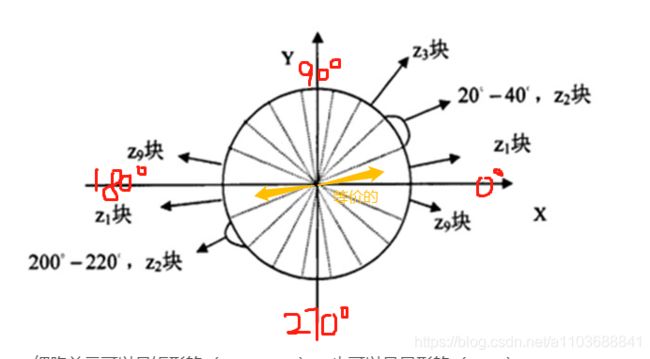
- 角度关系:
- 梯度幅度关系:
#计算梯度角度
#加0.00000001防止0除报错
grad_direction = np.arctan(vertical_gradient/(horizontal_gradient+0.000000001))
#弧度转角度
grad_direction = np.rad2deg(grad_direction)
#这边是定义180后的角度和0度拼起来,比如190度算10度
grad_direction = grad_direction%180
#计算梯度幅度
horizontal_gradient_square = np.power(horizontal_gradient, 2)
vertical_gradient_square = np.power(vertical_gradient, 2)
sum_squares = horizontal_gradient_square + vertical_gradient_square
grad_magnitude = np.sqrt(sum_squares)
plt.figure()
plt.subplot(2,1,1)
plt.title('图像角度直接显示,最大180')
plt.imshow(grad_direction, cmap = plt.cm.gray)
plt.subplot(2,1,2)
plt.title('图像幅度直接显示,最大可能')
plt.imshow(grad_magnitude, cmap = plt.cm.gray)
plt.show()结果如下:
6.统计每个cell的特征量->统计cell直方图信息
6.1 创建一个cell(这里刚好我们图片大小就等于我们的cell大小,我这个是特例)
cell_direction = grad_direction[:cell_size,:cell_size]
cell_magnitude = grad_magnitude[: cell_size,:cell_size]
plt.figure()
plt.subplot(2,1,1)
plt.imshow(cell_direction ,cmap= plt.cm.gray)
plt.subplot(2,1,2)
plt.imshow(cell_magnitude, cmap= plt.cm.gray)
plt.show()结果如下:
6.2 对cell进行统计->统计cell直方图信息
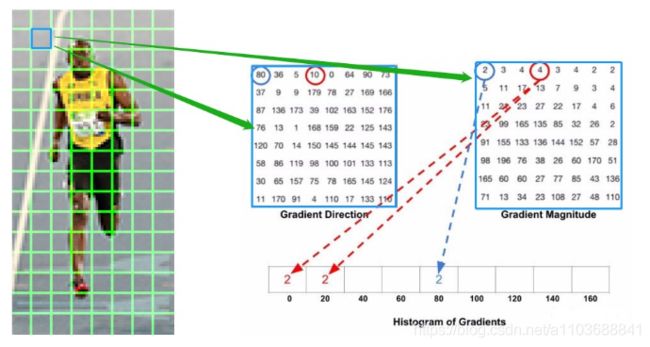
- 角度分类策略:(和我的是有些许区别,我不是从0开始)
- 统计策略:(别人的示意图是8*8,左边是梯度方向,右边是梯度幅度,下边是分类结果)
print('cell尺寸是{}*{}'.format(cell_size,cell_size))
hist_bins = np.array([10,30,50,70,90,110,130,150,170])
print('用来统计角度的数值有:',hist_bins)
HOG_cell_hist = np.zeros(shape=(hist_bins.size))
print('对应统计角度的计数',HOG_cell_hist,'\n')
for row_idx in range(cell_size):
for col_idx in range(cell_size):
print('当前处理的是第{}行,第{}列。这是全部数据中的第{}个像素'.format(row_idx,col_idx,
row_idx*cell_size+col_idx+1))
#取出当前的梯度和方向
curr_direction = cell_direction[row_idx, col_idx]
curr_magnitude = cell_magnitude[row_idx, col_idx]
print('当前这个像素的梯度方向是{},梯度幅度是{}'.format(curr_direction,curr_magnitude))
diff = np.abs(curr_direction - hist_bins)
print("用绝对值来判断当前梯度方向和谁最接近,差值是:\n",diff)
#当梯度角度比最小还小的情况
if curr_direction < hist_bins[0]:
first_bin_idx = 0
second_bin_idx = hist_bins.size-1
print('小于{}的角度我们直接夹杂最小和最大的两边,最小索引是{}最大索引是{}\n'.format(hist_bins[0],
first_bin_idx,second_bin_idx))
#当梯度角度比最大还大的情况
elif curr_direction > hist_bins[-1]:
first_bin_idx = hist_bins.size-1
second_bin_idx = 0
print('大于{}的角度我们直接夹杂最大和最小的两边,最大索引是{}最小索引是{}\n'.format(hist_bins[-1],
first_bin_idx,second_bin_idx))
#当梯度角度在最大和最小两者之间的情况
else:
#绝对值最小,离这个距离最近
first_bin_idx = np.where(diff == np.min(diff))[0][0]
print('绝对值小代表距离最近,最近的索引值是:',first_bin_idx)
#用余数除%hist_bins.size是为了循环,让头尾接在一起,这里其实我们可以屏蔽,
#因为我们对最大和最小的情况单独做了判断
temp = hist_bins[[(first_bin_idx-1)%hist_bins.size, (first_bin_idx+1)%hist_bins.size]]
print('俩边衔接最近的对应索引是:',\
(first_bin_idx-1)%hist_bins.size, (first_bin_idx+1)%hist_bins.size)
print('根据最近的两边索引提取出来的角度是:',temp)
temp2 = np.abs(curr_direction - temp)
print('再使用绝对值求解一次最近的这两边角度值,差值是{}'.format(temp2))
res = np.where(temp2 == np.min(temp2))[0][0]
print('第二次最近的索引是{},0是前一个,1是后一个'.format(res))
if res == 0 and first_bin_idx != 0:
second_bin_idx = first_bin_idx-1
else:
second_bin_idx = first_bin_idx+1
print('所以最近的第二个索引确定是{}'.format(second_bin_idx))
first_bin_value = hist_bins[first_bin_idx]
second_bin_value = hist_bins[second_bin_idx]
print('最终确定第一个最近的角度是{},第二个是{}'.format(first_bin_value,second_bin_value))
HOG_cell_hist[first_bin_idx] = HOG_cell_hist[first_bin_idx] + \
(np.abs(curr_direction - first_bin_value)/(180.0/hist_bins.size)) * curr_magnitude
HOG_cell_hist[second_bin_idx] = HOG_cell_hist[second_bin_idx] + \
(np.abs(curr_direction - second_bin_value)/(180.0/hist_bins.size)) * curr_magnitude
print('按梯度方向偏的多少给,给两边分类梯度幅度,当前分配完是:\n{}\n'.format(HOG_cell_hist))
print('最终计数',HOG_cell_hist)结果如下:
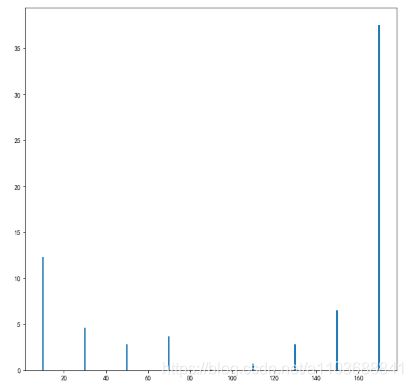
6.3 显示一下统计量
plt.figure()
plt.bar(x=hist_bins, height=HOG_cell_hist, align="center", width=0.8)
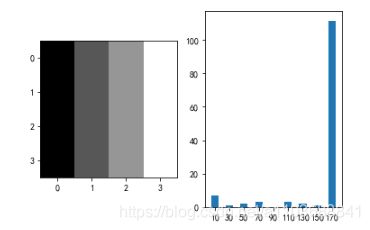
plt.show()结果如下:
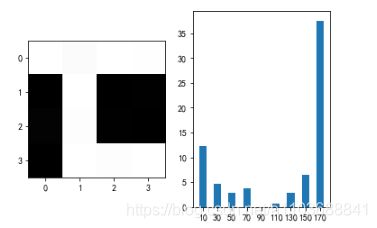
6.4 cell的物理意义
可以看到0-170方向的角度非常大,可以理解为这个cell是整体是横向方向上落差最大,效果不是很明显。
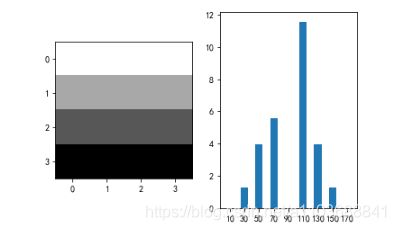
下面来看看效果明显的,可以看到那个角度统计量大,那么这个cell在哪个方向落差大。
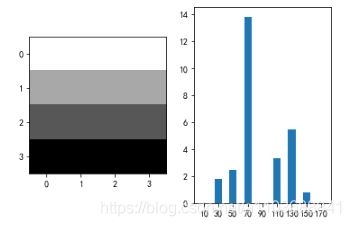
这里有个bug,因为tan的90°是间断点,所以我们求不出90°这个角度,我们可以使用sin或者cos函数进行优化,优化部位如下:
def gradient_magnitude_direction(horizontal_gradient, vertical_gradient):
horizontal_gradient_square = numpy.power(horizontal_gradient, 2)
vertical_gradient_square = numpy.power(vertical_gradient, 2)
sum_squares = horizontal_gradient_square + vertical_gradient_square
grad_magnitude = numpy.sqrt(sum_squares)
grad_direction = numpy.arcsin(vertical_gradient/grad_magnitude)
grad_direction = numpy.rad2deg(grad_direction)
grad_direction = grad_direction%180
return grad_magnitude,grad_direction结果如下,效果不是太好: