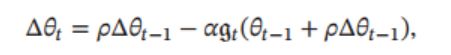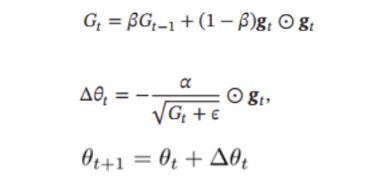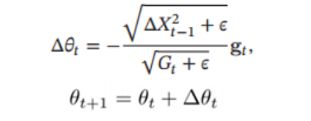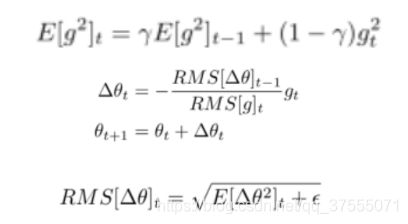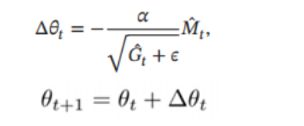【超详细】对比10种优化函数BGD、SGD、mini-batch GD、Momentum、NAG、Adagrad、RMSProp、Adadelta、Adam、AMSgrad
在实践中常用到一阶优化函数,典型的一阶优化函数包括 BGD、SGD、mini-batch GD、Momentum、Adagrad、RMSProp、Adadelta、Adam 等等,一阶优化函数在优化过程中求解的是参数的一阶导数,这些一阶导数的值就是模型中参数的微调值。另外,近年来二阶优化函数也开始慢慢被研究起来,二阶方法因为计算量的问题,现在还没有被广泛地使用。
深度学习模型的优化是一个非凸函数优化问题,这是与凸函数优化问题对应的。对于凸函数优化,任何局部最优解即为全局最优解。几乎所有用梯度下降的优化方法都能收敛到全局最优解,损失曲面如下:

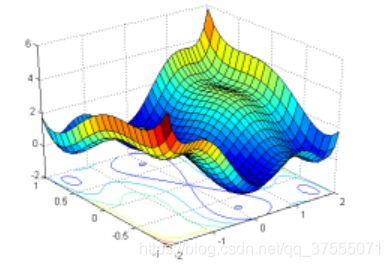
而非凸函数优化问题则可能存在无数个局部最优点,损失曲面如下,可以看出有非常多的极值点,有极大值也有极小值。
本文将从原理、公式、代码、loss曲线图、优缺点等方面详解论述:
- 一、BGD/SGD/mini-batch GD
- 1.1 BGD
- 1.2 SGD
- 1.3 Mini-batch GD
- 1.4 GD法的缺点
- 二、Momentum/NAG
- 2.1 Momentum
- 2.2 NAG
- 三、Adagrad/RMSProp/Adadelta
- 3.1 Adagrad
- 3.2 RMSProp
- 3.3 AdaDelta
- 四、Adam\AMSgrad
- 4.1 Adam
- 4.2 AMSgrad
- 五、不同优化函数比较
- 六、pytorch不同优化函数的定义
一、BGD/SGD/mini-batch GD
梯度下降算法主要有BGD、SGD、mini-batch GD,后面还有梯度下降算法的改进,即Momentum、Adagrad 等方法
1.1 BGD
BGD(Batch gradient descent,批量梯度下降),是拿所有样本的loss计算梯度来更新参数的,更新公式如下:
θ = θ − η ⋅ ∇ θ J ( θ ) \theta=\theta-\eta· \nabla_\theta J(\theta) θ=θ−η⋅∇θJ(θ)
在有的文献中,称GD是拿所有样本的loss计算梯度来更新参数,也就是全局梯度下降,和这里的BGD是一个意思
其中, θ \theta θ为要更新的参数,即weight、bias; η \eta η 为学习率; J J J为损失函数,即 loss function ; ∇ θ J ( θ ) \nabla_\theta J(\theta) ∇θJ(θ) 是指对 loss function 的 θ \theta θ 求梯度。
令 Δ θ t = − η ⋅ ∇ θ J ( θ ) \Delta\theta_t=-\eta· \nabla_\theta J(\theta) Δθt=−η⋅∇θJ(θ),则 θ t + 1 = θ t + Δ θ t \theta_{t+1}=\theta_{t}+\Delta\theta_t θt+1=θt+Δθt, θ 1 \theta_{1} θ1 即初始化的weight、bias。
写成伪代码如下:
# all_input和all_target是所有样本的特征向量和label
for i in range(epochs):
optimizer.zero_grad()
output = model(all_input)
loss = loss_fn(output,all_target)
loss.backward()
optimizer.step()
在loss的等值线图中,随着 weight 的变化loss降低的曲线走向(红线)如下所示:
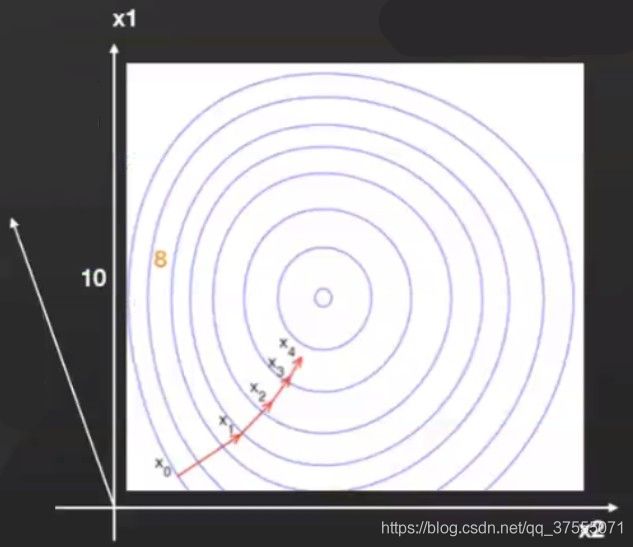
其中 x1是纵轴,x2是横轴 ; w e i g h t = [ x 1 , x 2 ] weight=[x1,x2] weight=[x1,x2] ,即两个坐标轴对应的点; X i = [ x 1 i , x 2 i ] X_i=[x1_i,x2_i] Xi=[x1i,x2i],即weight不同时刻的取值; X 0 = [ x 1 0 , x 2 0 ] X_0=[x1_0,x2_0] X0=[x10,x20]是weight的初始化值。
从上图中可以看出,BGD的loss曲线走向相对平滑,每一次优化都是朝着最优点走。
由于BGD在每次计算损失值时都是针对整个参与训练的样本而言的,所以会出现内存装不下,速度也很慢的情况。能不能一次取一个样本呢?于是就有了随机梯度下降(Stochastic gradient descent),简称 sgd。
1.2 SGD
SGD(Stochastic gradient descent,随机梯度下降)是一次拿一个样本的loss计算梯度来更新参数,其更新公式如下:

其中, x ( i ) x^{(i)} x(i) 是第一个样本的特征向量, y ( i ) y^{(i)} y(i) 是第i个样本的真实值。
也可以写成如下形式:
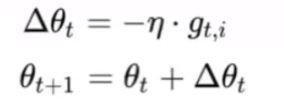
其中, g t , i g_{t,i} gt,i 是第i个样本的梯度。
写成伪代码如下:
for i in range(epochs):
# batch=1,每次从dataset取出一个样本
for input_i,target_i in dataset:
optimizer.zero_grad()
output = model(all_input)
loss = loss_fn(output,all_target)
loss.backward()
optimizer.step()
在loss的等值线图中,随着 weight 的变化loss降低的曲线走向如下所示:

从上图中可以看出,SGD的loss曲线走向是破浪式的,相对于BGD的方式,波动大,在非凸函数优化问题中,SGD可能使梯度下降到更好的另一个局部最优解,但从另一方面来讲,SGD的更新可能导致梯度一直在局部最优解附近波动。
SGD的不确定性较大,可能跳出一个局部最优解到另一个更好的局部最优解,也可能跳不出局部最优解,一直在局部最优解附近波动
由于同一类别样本的特征是相似的,因此某一个样本的特征能在一定程度代表该类样本,所以SGD最终也能够达到一个不错的结果,但是,SGD的更新方式的波动大,更新方向前后有抵消,存在浪费算力的情况。于是,就有了后来大家常用的小批量梯度下降算法(Mini-batch gradient descent)。
1.3 Mini-batch GD
Mini-batch GD(Mini-batch gradient descent,小批量梯度下降)是一次拿一个batch的样本的loss计算梯度来更新参数,其更新公式如下:
![]()
其中,batch_size=n。
写成伪代码如下:
for i in range(epochs):
# batch_size=n,每次从dataset取n个样本
for input,target in dataset:
optimizer.zero_grad()
output = model(all_input)
loss = loss_fn(output,all_target)
loss.backward()
optimizer.step()
在loss的等值线图中,随着 weight 的变化loss降低的曲线走向如下所示:

从上图可以看出,mini-batch GD 的loss走向曲线在BGD和SGD之间,mini-batch GD 既解决了SGD更新方式波动大的问题,又可以尽量去计算多个样本的loss,提高参数的更新效率。
1.4 GD法的缺点
梯度下降算法虽然取得了一定的效果,但是仍然有以下缺点:
- 学习率大小比较难缺难确定,需要反复去试
- 学习率不够智能,对每个参数的各个维度一视同仁
- mini-batch GD算法中,虽然一定程度上提高参数的更新效率,并没有完全解决SGD中的问题,即更新方向仍然前后有抵消,仍然有浪费算力的情况
- SGD和mini-batch GD由于每次参数训练的样本是随机选取的,模型会受到随机训练样本中噪声数据的影响,又因为有随机的因素,所以也容易导致模型最终得到局部最优解。
二、Momentum/NAG
知道了GD法的缺点,动量法通过之前积累梯度来替代真正的梯度从而避免GD法浪费算力的缺点,加快更新速度,我们现在来看动量法(momentum)和其改进方法NAG吧。
2.1 Momentum
在使用梯度下降算法的时,刚开始的时候梯度不稳定,波动性大,导致做了很多无用的迭代,浪费了算力,动量法(momentum)解决SGD/mini-batch GD中参数更新震荡的问题,通过之前积累梯度来替代真正的梯度,从而加快更新速度,其更新公式如下:
υ t = γ υ t − 1 + η ⋅ ∇ θ J ( θ ) θ = θ − υ t \begin{array}{l} \upsilon_t=\gamma\upsilon_{t-1}+\eta· \nabla_\theta J(\theta)\\ \theta=\theta-\upsilon_t \end{array} υt=γυt−1+η⋅∇θJ(θ)θ=θ−υt
其中, θ \theta θ是要更新的参数即weight, ∇ θ J ( θ ) \nabla_\theta J(\theta) ∇θJ(θ)是损失函数关于weight的梯度, γ \gamma γ为动量因子,通常设为0.9; η \eta η 为学习率。这里新出现了一个变量 υ \upsilon υ,对应物理上的速度。
也可以写成下面的形式(不常用):
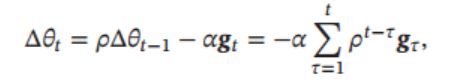
其中, ρ \rho ρ为动量因子,通常设为0.9; α \alpha α为学习率。
只看公式可能不好理解,我们来代入计算下吧。
假设 η \eta η 学习率为0.1,用 g 表示损失函数关于weight的梯度,则可计算如下:
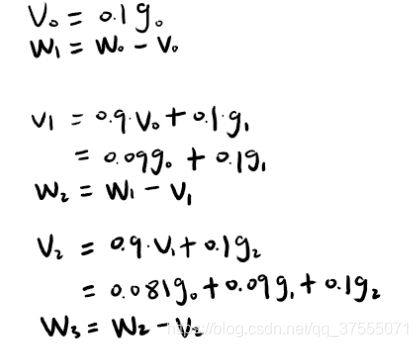
动量法(momentum)更新示意图如下所示:
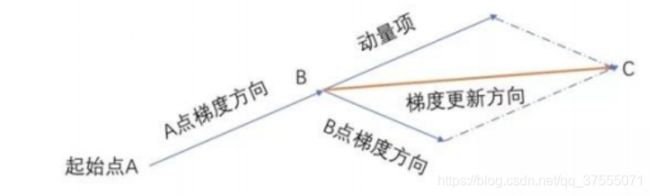
这样, 每个参数的实际更新差值取决于最近一段时间内梯度的加权平均值。当某个参数在最近一段时间内的梯度方向不一致时, 其真实的参数更新幅度变小,增加稳定性; 相反, 当在最近一段时间内的梯度方向都一致时, 其真实的参数更新幅度变大, 起到加速作用。
一般而言, 在迭代初期, 梯度方向都比较一致, 动量法会起到加速作用, 可以更快地到达最优点。在迭代后期, 梯度方向会不一致, 在收敛值附近振荡, 动量法会起到减速作用, 增加稳定性。动量法也能解决稀疏梯度和噪声问题,这个到Adam那里会有详细解释。
2.2 NAG
NAG(Nesterov Accelerated Gradient,Nesterov加速梯度)是一种对动量法的改进方法, 也称为 Nesterov 动量法(Nesterov Momentum)。其公式如下:
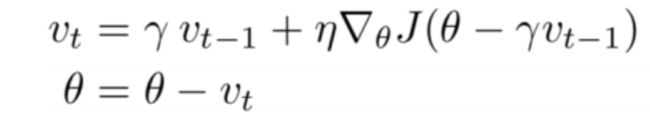
其中, ∇ θ J ( θ − γ υ t − 1 ) \nabla_\theta J(\theta-\gamma\upsilon_{t-1}) ∇θJ(θ−γυt−1)是损失函数关于下一次(提前点)weight的梯度。
由于momentum刚开始时梯度方向都比较一致,收敛较快,但是到后期,由于momentum惯性的存在,很可能导致在loss极值点的附近来回震荡,而NAG向前计算了一次梯度,当梯度方向快要改变的时候,它提前获得了该信息,从而减弱了这个过程,再次减少了无用的迭代,并保证能顺利更新到loss的极小值点。
三、Adagrad/RMSProp/Adadelta
在神经网络的学习中,学习率( η \eta η)的值很重要。学习率过小,会导致学习花费过多时间;反过来,学习率过大,则会导致学习发散而不能正确进行。
在关于学习率的有效技巧中,有一种被称为学习率衰减(learning rate decay)的方法,即随着学习的进行,使学习率逐渐减小。实际上,一开始“多”学,然后逐渐“少”学的方法,在神经网络的学习中经常被使用。逐渐减小学习率的想法,相当于将“全体”参数的学习率值一起降低。而AdaGrad进一步发展了这个想法,针对“一个一个”的参数,赋予其“定制”的值,现在我们来看Adagrad/RMSProp/Adadelta吧。
3.1 Adagrad
AdaGrad(Adaptive Grad,自适应梯度)为参数的每个参数自适应地调整学习率,让不同的参数具有不同的学习率,其公式如下:
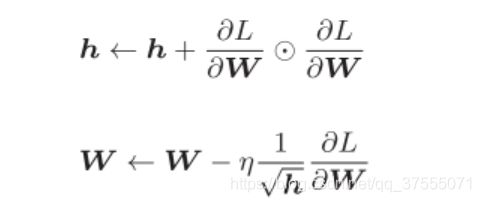
其中,W表示要更新的权重参数, ∂ L ∂ W \frac{{\partial L}}{{\partial W}} ∂W∂L表示损失函数关于W的梯度, η \eta η表示学习率,这里新出现了变量 h h h,它保存了以前的所有梯度值的平方和, ⊙ \odot ⊙表示对应矩阵元素的乘法。然后,在更新参数时,通过乘以 1 h \frac{1}{\sqrt h} h1,就可以调整学习的尺度。这意味着,参数的元素中变动较大(被大幅更新)的元素的学习率将变小。也就是说,可以按参数的元素进行学习率衰减,使变动大的参数的学习率逐渐减小。
其中, g τ ∈ R g_\tau \in R gτ∈R 是第 τ \tau τ次迭代时的梯度, α \alpha α为初始的学习率, ε \varepsilon ε是为了保持数值稳定性而设置的非常小的常数, 一般取值 e − 7 e^{−7} e−7 到 e − 10 e^{−10} e−10,此外, 这里的开平方、 除、 加运算都是按元素进行的操作。
由于Adagrad学习率衰减用了所有的梯度,如果在经过一定次数的迭代依然没有找到最优点时,累加的梯度幅值是越来越大的,导致学习率越来越小, 很难再继续找到最优点,为了改善这个问题,从而提出RMSProp算法。
3.2 RMSProp
与AdaGrad不同,RMSProp(Root Mean Square Propagation,均方根传播) 方法并不是将过去所有的梯度一视同仁地相加,而是逐渐地遗忘过去的梯度,在做加法运算时将新梯度的信息更多地反映出来,这种操作从专业上讲,称为“指数移动平均”,呈指数函数式地减小过去的梯度的尺度。
其中, β \beta β 为衰减率, 一般取值为 0.9, α \alpha α为初始的学习率, 比如 0.001。
从上式可以看出, RMSProp 算法和 AdaGrad 算法的区别在于 G t G_t Gt 的计算由累积方式变成了指数衰减移动平均。在迭代过程中, 并且,每个参数的学习率并不是呈衰减趋势, 既可以变小也可以变大(把 β \beta β设的更小些,每个参数的学习率就呈变大趋势)。
这里不得不提一下RProp,Rprop可以看做 RMSProp的简单版,它是依据符号来改变学习率的大小:当最后两次梯度符号一样,增大学习率,当最后两次梯度符号不同,减小学习率。
3.3 AdaDelta
AdaDelta 与 RMSprop 算法类似, AdaDelta 算法也是通过梯度平方的指数衰减移动平均来调整学习率。此外, AdaDelta 算法还引入了每次参数更新差值Δ 的平方的指数衰减权移动平均。
第 t 次迭代时, 参数更新差值 Δ 的平方的指数衰减权移动平均为
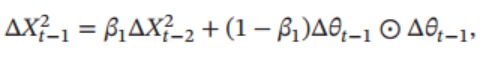
AdaDelta 算法的参数更新公式为:
其中 G t G_t Gt 的计算方式和 RMSprop 算法一样 , Δ X t − 1 2 \Delta X_{t - 1}^2 ΔXt−12 为参数更新差值 Δ 的指数衰减权移动平均。
从上式可以看出, AdaDelta 算法将 RMSprop 算法中的初始学习率 改为动态计算的 Δ X t − 1 2 \sqrt {\Delta X_{t - 1}^2} ΔXt−12 ,在一定程度上平抑了学习率的波动。除此之外,AdaDelta连初始的学习率都不要设置了,提升了参数变化量的自适应能力。
除此之外,AdaDelta公式还有一个常用的表示方法:
四、Adam\AMSgrad
现在来介绍比较好用的方法Adam和其改进方法AMSgrad。
4.1 Adam
Adam 算法 (Adaptive Moment Estimation Algorithm)可以看作动量法和 RMSprop 算法的结合, 不但使用动量作为参数更新方向, 而且可以自适应调整学习率。
Adam 算法一方面计算梯度平方 g t 2 g^2_t gt2 的指数衰减移动平均(和 RMSprop 算法类似), 另一方面计算梯度 g t g_t gt 的指数衰减移动平均 (和动量法类似),如下所示:

其中 β 1 \beta_1 β1 和 β 2 \beta_2 β2 分别为两个移动平均的衰减率, 通常取值为 β 1 \beta_1 β1 = 0.9, β 2 \beta_2 β2 = 0.999。 我们可以把 M t M_t Mt 和 G t G_t Gt 分别看作梯度的均值(一阶矩估计)和未减去均值的方差(二阶矩估计)。其中, M t M_t Mt 来自momentum,用来稳定梯度, G t G_t Gt 来自RMSProp,用来是梯度自适应化。
对 M t M_t Mt 和 G t G_t Gt偏差进行修正:
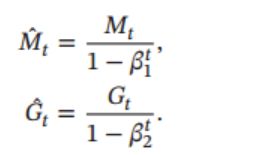
其中,其中学习率 $\alpha $ 通常设为 0.001, 并且也可以进行衰减, 比如 α t = α 0 t \alpha_t=\frac{\alpha_{0}}{\sqrt t} αt=tα0 。
Adam, 结合了 动量法 和 RMSProp 算法最优的性能,它还是能提供解决稀疏梯度和噪声问题的优化方法,在深度学习中使用较多。这里解释一下为什么Adam能够解决稀疏梯度和噪声问题:稀疏梯度是指梯度较多为0的情况,由于adam引入了动量法,在梯度是0的时候,还有之前更新时的梯度存在(道理跟momentum一样),还能继续更新;噪声问题是对于梯度来说有一个小波折(类似于下山时路不平有个小坑)即多个小极值点,可以跨过去,不至于陷在里面。
Adam 算法是 RMSProp 算法与动量法的结合, 因此一种自然的 Adam 算法的改进方法是引入 Nesterov 加速梯度, 称为Nadam 算法
这里思考一个问题:为什么对Adam偏差进行修正?
网上没找到好的解释,那来看一下原文吧!

大致意思是说:刚开始,我们任意初始化了一个 m 0 m_0 m0(注意:一般 m 0 m_0 m0初始化为0,在Momentum算法中也是),并且根据公式 m t = β m t − 1 + ( 1 − β ) g t m_t=\beta m_{t-1}+(1-\beta)g_t mt=βmt−1+(1−β)gt更新公式,得到 m 1 m_1 m1,可以明显的看到,第一步更新严重依赖初始化的 m 0 m_0 m0,这样可能会造成严重的偏差。
为了纠正这个,我们需要移除这个初始化 m 0 m_0 m0(偏置)的影响,例如,可以把 m 1 = β m 0 + ( 1 − β ) g 1 m_1=\beta m_{0}+(1-\beta)g_1 m1=βm0+(1−β)g1中的 β m 0 \beta m_{0} βm0从 m 1 m_1 m1移除(即 m 1 − β m 0 m_1-\beta m_0 m1−βm0),并且除以( 1 − β 1-\beta 1−β),这样公式就变为了 m ^ = m 1 − β m 0 1 − β \hat{m}=\frac{m_1-\beta m_0}{1-\beta} m^=1−βm1−βm0,当 m 0 m_0 m0=0时, m t ^ = m t 1 − β t \hat{m_t}=\frac{m_t}{1-\beta^t} mt^=1−βtmt。同理,对于 G t G_t Gt也是如此。
总的来说,在迭代初期, M t M_t Mt 和 G t G_t Gt的更新严重依赖于初始化的 M 0 = 0 M_0=0 M0=0、 G 0 = 0 G0=0 G0=0,当初始化 M t M_t Mt 和 G t G_t Gt都为0时, M t M_t Mt 和 G t G_t Gt都会接近于0,这个估计是有问题的,可能会造成严重的偏差(即可能使学习率和方向与真正需要优化的学习率和方向严重偏离),所以,我需要移除这个初始化的 M 0 M_0 M0 和 G 0 G0 G0(偏置)的影响, 故需要对偏差进行修正。
上面说了这么多理论,分析起来头头是道,各种改进版本似乎各个碾压 SGD 算法。但是否真的如呢?此外,Adam看起来都这么厉害了,以后的优化函数都要使用Adam吗?
来看一下下面的实验:
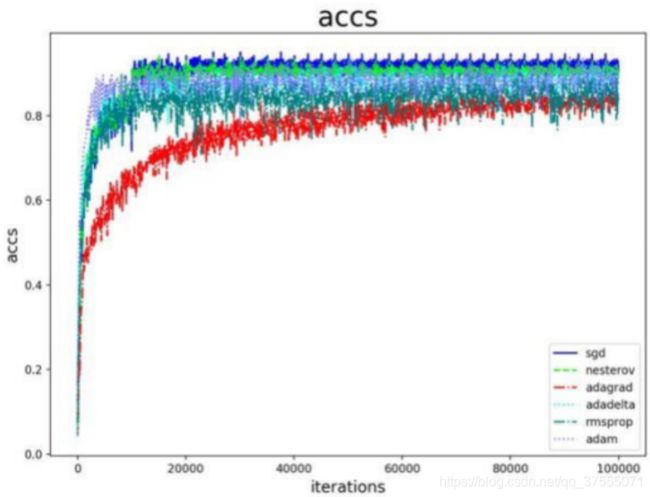
所有方法都采用作者们(原文)的默认配置,并且进行了参数调优,不好的结果就不拿出来了。
- nesterov 方法,与 sgd 算法同样的配置。
- adam 算法,m1=0.9,m2=0.999,lr=0.001。
- rms 算法,rms_decay=0.9,lr=0.001。
- adagrad,adadelta 学习率不敏感。
看起来好像都不如 SGD 算法,实际上这是一个很普遍的现象,各类开源项目和论文都能够印证这个结论。总体上来说,改进方法降低了调参工作量,只要能够达到与精细调参的 SGD 相当的性能,就很有意义了,这也是 Adam 流行的原因。但是,改进策略带来的学习率和步长的不稳定还是有可能影响算法的性能,因此这也是一个研究的方向,不然哪来这么多Adam 的变种呢。
这里引用一位清华博士举的例子:很多年以前,摄影离普罗大众非常遥远。十年前,傻瓜相机开始风靡,游客几乎人手一个。智能手机出现以后,摄影更是走进千家万户,手机随手一拍,前后两千万,照亮你的美(咦,这是什么乱七八糟的)。但是专业摄影师还是喜欢用单反,孜孜不倦地调光圈、快门、ISO、白平衡……一堆自拍党从不care的名词。技术的进步,使得傻瓜式操作就可以得到不错的效果,但是在特定的场景下,要拍出最好的效果,依然需要深入地理解光线、理解结构、理解器材。优化算法大抵也如此,大家都是殊途同归,只是相当于在SGD基础上增加了各类学习率的主动控制。如果不想做精细的调优,那么Adam显然最便于直接拿来上手。
原文在Adam那么棒,为什么还对SGD念念不忘 (2)—— Adam的两宗罪
Adam那么棒,也不是没有缺点,继续往下面看!
4.2 AMSgrad
ICLR 2018 最佳论文提出了 AMSgrad 方法,研究人员观察到 Adam 类的方法之所以会不能收敛到很好的结果,是因为在优化算法中广泛使用的指数衰减方法会使得梯度的记忆时间太短。
在深度学习中,每一个 mini-batch 对结果的优化贡献是不一样的,有的产生的梯度特别有效,但是也一视同仁地被时间所遗忘。
具体的做法是使用过去平方梯度的最大值来更新参数,而不是指数平均。其公式如下:

五、不同优化函数比较
(1)不同优化函数的loss下降曲线如下:
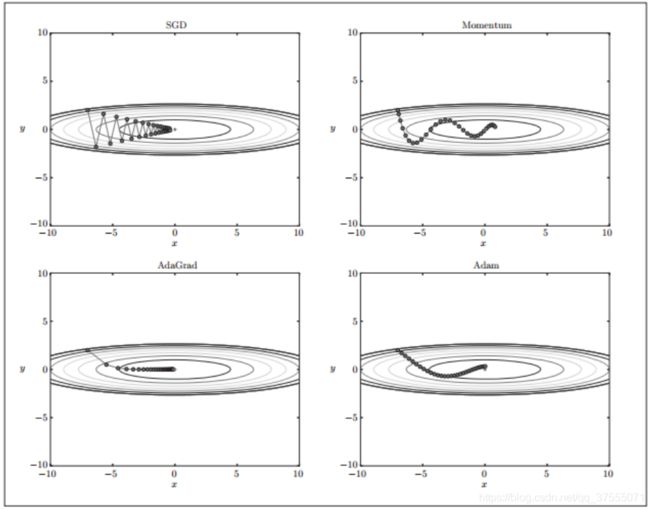
(2)不同优化函数在 MNIST 数据集上收敛性的比较(学习率为0.001, 批量大小为 128):
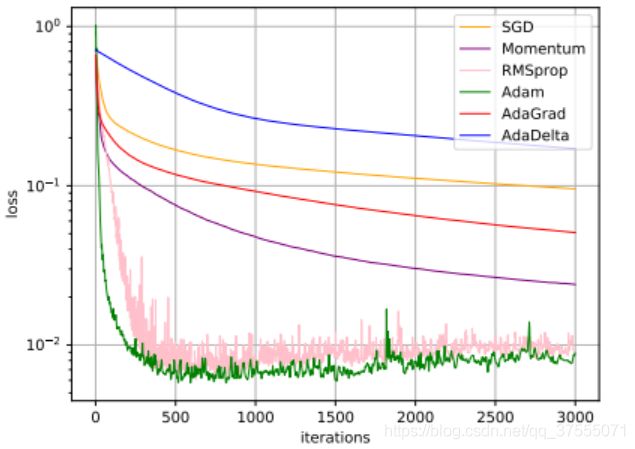
(3)不同优化函数配对比较
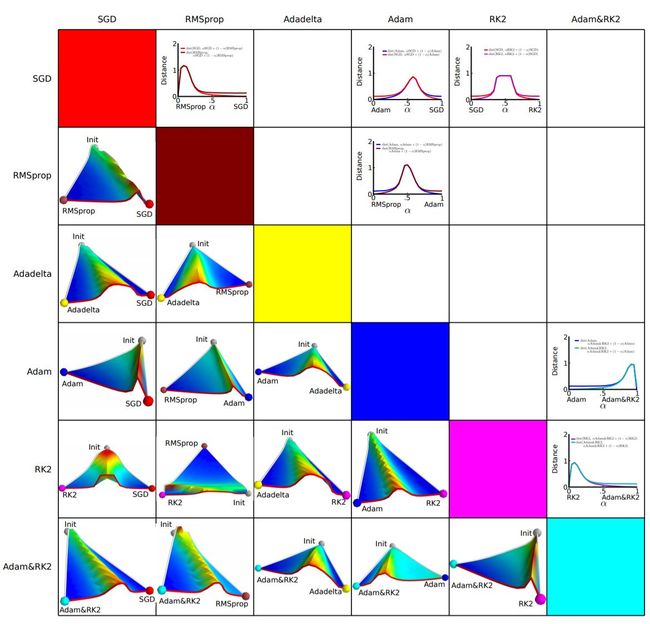
横纵坐标表示降维后的特征空间,区域颜色则表示目标函数值的变化,红色是高原,蓝色是洼地。他们做的是配对儿实验,让两个算法从同一个初始化位置开始出发,然后对比优化的结果。可以看到,几乎任何两个算法都走到了不同的洼地,他们中间往往隔了一个很高的高原。这就说明,不同算法在高原的时候,选择了不同的下降方向。
这里参考 Adam那么棒,为什么还对SGD念念不忘 (3)—— 优化算法的选择与使用策略述
六、pytorch不同优化函数的定义
这里介绍几种常用优化函数的参数定义和解释
(1)torch.optim.SGD
- lr 学习率,用于控制梯度更新的快慢,如果学习速率过快,参数的更新跨步就会变大,极易出现震荡;如果学习速率过慢,梯度更新的迭代次数就会增加,参数更新、优化的时间也会变长,所以选择一个合理的学习速率是非常关键的。
- momentum 动量因子,介于[0,1]之间,默认为0,一般设为0.9,当某个参数在最近一段时间内的梯度方向(即与动量 υ \upsilon υ方向)不一致时, 其真实的参数更新幅度变小,增加稳定性; 相反, 当在最近一段时间内的梯度方向都一致时, 其真实的参数更新幅度变大, 起到加速作用。
- weight_decay 权重衰减(L2惩罚),默认为0,来看下原文吧:

大致意思是说:为了避免过拟合,在这里增加了一个L2惩罚项,推到如下:
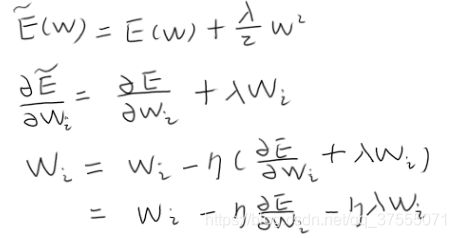
其中, η \eta η为学习率,而 η λ \eta\ \lambda η λ 就是weight_decay,不过pytorch让用户可以自由设置,有了更大的自由度 - nesterov,布尔类型,默认为False,设为True,可使用NAG动量
使用方式:
optimizer = torch.optim.SGD(model.parameters(), lr=0.1, momentum=0.9)
for i in range(epochs):
# batch_size=n,每次从dataset取n个样本
for input,target in dataset:
optimizer.zero_grad()
output = model(all_input)
loss = loss_fn(output,all_target)
loss.backward()
optimizer.step()
(2)torch.optim.Adagrad
- lr-decay 学习率衰减,学习率衰减公式如下所示:

其中, l r i lr_i lri为第i次迭代时的学习率, l r s t a r t lr_start lrstart为原始学习率,decay为一个介于[0.0, 1.0]的小数。可以看到,decay越小,学习率衰减地越慢,当decay = 0时,学习率保持不变。decay越大,学习率衰减地越快,当decay = 1时,学习率衰减最快。 - eps,相当于 ε \varepsilon ε,是为了保持数值稳定性而设置的非常小的常数, 一般取值 e − 7 e^{−7} e−7 到 e − 10 e^{−10} e−10
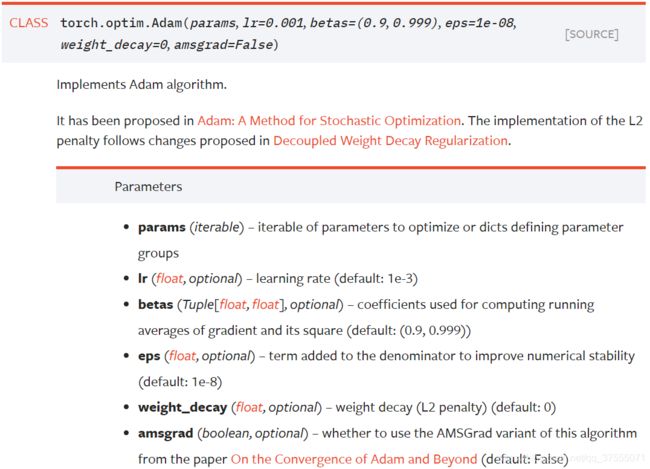
(3)torch.optim.Adam
- betas,默认值(0.9,0.999),即Adam里的 β 1 \beta_1 β1、 β 2 \beta_2 β2
- amsgrad,是否启用Adam的改进方法AMSgrad,默认为False
这里只介绍了需要注意的几个优化函数,更多函数定义,请查阅pytorch官方文档
【参考文档】
神经网络与深度学习-邱锡鹏著
有三AI-深度学习视觉算法工程师指导手册
深度学习入门:基于pytorch的理论与实现-陆宇杰译
深度学习之pytorch实战计算机视觉-唐进民著
optim.sgd学习参数