TensorFlow游乐园介绍及其神经网络训练过程

       TensorFlow游乐场是一个通过网页浏览器就可以训练简单神经网络。并实现了可视化训练过程的工具。游乐场地址为http://playground.tensorflow.org/

一、TensorFlow游乐园参数介绍      

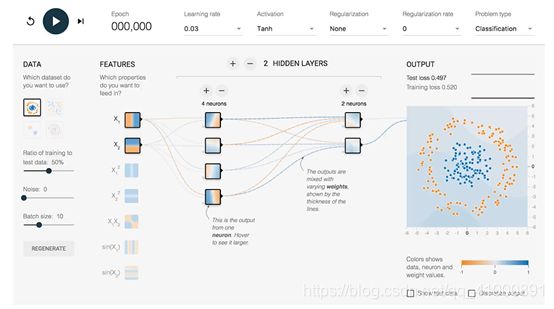
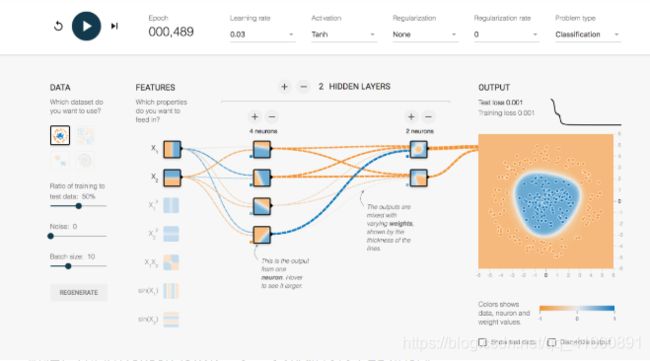
       打开游乐园可以看到有很多的默认参数：

      首先我们来解读一下顶部的一些参数：

       Epoch ---> 训练次数。

       learning rate ---> 学习率（是一个超参数，在梯度下降算法中会用到；学习率是人为根据实际情况来设定）。

       Activation ---> 激活函数（默认为非线性函数Tanh；如果对于线性分类问题，这里可以不使用激活函数）。

       Regularization ---> 正则化（正则化是利用范数解决过拟合的问题，这里咱不讨论）。

       Regularization rate ---> 正则率（这里不使用正则化所以无需考虑）。

       Problem type ---> 问题类型（在这里我们要解决的是一个二分类问题，简单解释一下分类问题是指，给定一个新的模式，根据训练集推断它所对应的类别（如：+1，-1），是一种定性输出，也叫离散变量预测；回归问题是指，给定一个新的模式，根据训练集推断它所对应的输出值（实数）是多少，是一种定量输出，也叫连续变量预测；在这里我们属于分类问题）

       其次是下发的一些模块：

       DATA ---> 数据集类型（这里提供了四种数据集，我们默认选中第一种；被选中的数据也会显示在最右侧的OUTPUT中；在这个数据中，我们可以看到二维平面上有蓝色和黄色的小点；每一个小点代表一个样例例子；点的颜色代表样例的标签；因为只有两种颜色，所以这里是一个二分类问题；在这里我们以判断某工厂零件是否合格为例子来说明，那么黄色就代表不合格零件，蓝色就代表合格零件）。

       FEATURES ---> 特征向量（为了将一个实际问题对应到空间中的点，我们需要提取特征。在这里我们可以用零件的长度和质量来大致描述；所以这里x1就代表零件长度，x2代表零件质量;特征向量是神经网络的输入）。

       HIDDEN LAYERS ---> 隐藏层（在输入和输出之间的神经网络称为隐藏层；一般神经网络的隐藏层越多这个神经网络越深；这里我们默认有一个隐藏层，这个隐藏层上有4个节点）。

       OUTPUT ---> 输出（显示区分平面以及训练数据）。

 

 二、以TensorFlow游乐园为例介绍神经网络训练过程

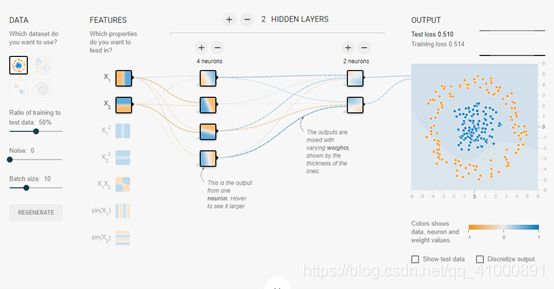
       图上每一个小格子代表神经网络中的一个神经元，每一条线代表神经元之间的连接。每一个节点和边都被涂上了或深或浅的颜色。但边的颜色和格子中的颜色含义有略微区别。每一条边代表了神经网络的一个权重（可以理解为一个参数），它可以理解为任意实数。神经网络就是利用反向传播算法对权重进行合理修改从而解决分类或者回归问题。边的颜色表现了权重的取值，当边颜色越深这个参数绝对值越大；当边越接近白色，这个参数绝对值趋于0。

       每一个节点上的颜色代表了这个节点的区分平面。在这里稍微解释一下区分平面的概念。如果我们把这个平面当成一个笛卡尔坐标系，这个平面上的每一个点就代表了（x1,x2）的一种取值。如果你觉得小图不太清楚，可以把鼠标放到输入节点x1上面，可以看到x1节点此时的区分平面就是Y轴。

       因为x1为输入层，输入层的输出值就是x1本身的值。所以当x1小于0时，这个节点输出为负，x1大于灵时节点输出为正。所以Y轴左侧都为橙色，右侧都是蓝色。同理x2的区分平面也很容易理解。
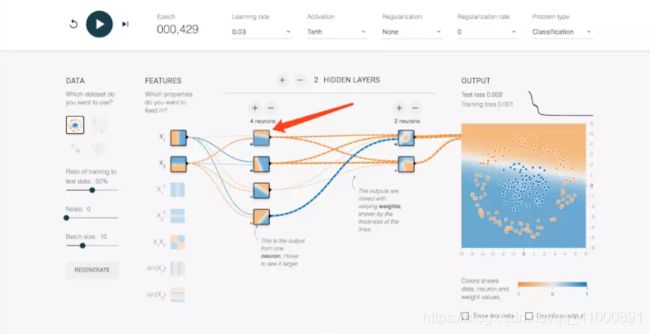
       现在我们来看隐藏层的节点，这里我们只有一个隐藏层，这个隐藏层上有四个节点。先来看第一个。这里我们把隐藏层节点1简称为h1。

       可以看到这个节点的区分平面是一条在x轴之上的斜线。为什么会发生这种情况？？这里就涉及到我们之前说的权重。在神经网络前向传播的过程中，后面节点的输入是之前与之相连的所有节点的加权和。我们仔细观察连线可以发现x1和h1的连线趋于白色，x2和h1是一条很明显的橙色线。把鼠标移到细线上可以看到权重的值，这里得到公式-0.12x1 + -0.73x2 = h1。所以得到了如图所示的一个区分平面。平面上方都是负值，下方都是正值。其它节点以此类推。在这里可以看到，权重对分类的影响至关重要。

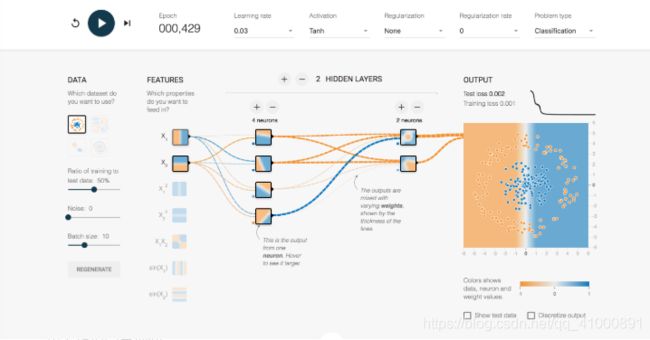
       最后我们来看隐藏层到输出层的输出。首先我们来看一下OUTPUT，如果最终要区分蓝色的点和橙色的点，我们的区分平面应该是一个闭合曲线。然而如果我们光靠加权和这种线性变换的话是没有办法准确圈出蓝色和橙色点的分界线。所以在隐藏层到输出层的过程我们增加了一个非线性激活函数Tanh，使得我们最后可以得到一个非线性的结果。综上神经网络解决一个分类问题大致可以分为：

       1.提取特征向量作为输入，比如说本例子中零件的长度和质量。

       2.定义神经网络结构。包括隐藏层数，激活函数等等。

       3.通过训练利用反响传播算法不断优化权重的值，使之达到最合理水平。

       4.使用训练好的神经网络来预测未知数据，这里训练好的网络就是指权重达到最优的情况。

      下面我们点击开始训练按钮，下图是训练489次后的情况。观察OUTPUT，这时模型其实已经很准确的进行了分类。