枚举与优化套路

ACM题集：https://blog.csdn.net/weixin_39778570/article/details/83187443

出自蓝桥学苑 GtDzx老师
#枚举与优化套路（1）
这里有一些非常常用的思路。1是二分，二分查找、二分搜索非常有效，一般是复杂度从O(N)降到O(logN)。使用范围也很广，我们会在后面专门拿出一节时间来讲。2是用Hash，空间换时间。此外还有一些常用的套路：比如双指针，Leetcode上对应的分类是two pointer，直译过来就是双指针，大概的思想就是滑动窗口。还比如前缀后缀和，也是空间换时间的思路

---

#枚举与优化套路（2）

使用map(红黑树)或者unoreder_map(哈希表),c++11支持,时间复杂度为O(logn)和O(1)

---

#枚举与优化套路（3）

使用map(红黑树)或者unoreder_map(哈希表),c++11支持,时间复杂度为O(logn)和O(1)

支持C++11

不支持C++11

#include 
#include 
using namespace std; 
int n, k, x, ans = 0;
set myset;
int main(){
	cin >> n >> k;
	for(int i=0; i> x;
		myset.insert(x);
	}
	for(set::iterator i=myset.begin(); i!=myset.end(); i++){
		if(myset.find((*i)+k) != myset.end()){ // (*)解引用
			ans++;
		}
	}
	cout << ans << endl;	
	return 0;
}

题目连接:hihoCoder的1494题

支持C++11

不支持C++11

#include 
#include 

---

#枚举与优化套路（4）

例题：蓝桥杯：四平方和、hihoCoder #1505题：小Hi和小Ho的礼物。

不支持C++11

#include 
#include 

有些同学可能会有疑问，就是f里保存的是c最小的解，会不会这个c比b小，不满足题目要求。比如N=30，我们枚举到a=1，b=2，这时f[25]=0，我们找到的解会是a=1, b=2, c=0, d=5。实际上不用担心这个问题。因为如果a=1, b=2, c=0, d=5是一个解，那么换一下顺序a=0, b=1, c=2, d=5也一定是一个解。并且a=0, b=1一定比a=1, b=2先枚举到（参考第17和18行），在这时就会求出a=0, b=1, c=2, d=5的解，然后程序结束了。

题目链接:hihoCoder #1505题：小Hi和小Ho的礼物。

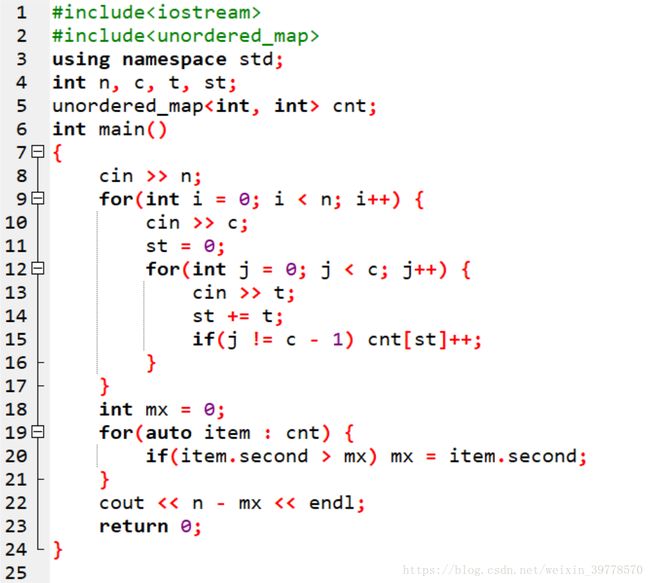
有了之前四平方和的基础。这道题我们很快就会想到一个类似的优化思路：首先预处理出来2袋金币数目和是某个值X一共有多少种选法。把预处理的结果存在哈希表里，记作cnt2[X]，表示选出2袋金币和是X有几种选法。然后只枚举i和j，也就是给小Hi的两袋金币。这样我们就知道金币的和应该是多少。通过查哈希表得到小Ho的两袋金币一共有多少种选法。
这个思路大致方向是对的，但是有个小问题。就是一袋金币不能既给小Hi又给小Ho。我们用样例来说明一下。样例是5袋金币，分别有1，1，2，2，2枚。那么一共有几种选法能选出总数是3枚的2袋金币呢？

从上图我们可以看到一共有6种选法。（注意ij是下标）现在假设我给小Hi的金币是第1袋和第3袋，(金币总数之和是3)那么这时给小Ho的2袋有几种选法呢？注意上面6种和是3的选法并不是都成立，因为第1袋和第3袋金币已经分给小Hi了，所以(1, 3)(1, 4)(1, 5)(2, 3)这四种组合都不能选，只剩下2种组合可选。
于是我们又有了新的问题：我现在选了第1袋和第3袋给小Hi，我知道金币和是3。我们怎么从金币和是3的6种选法里把包含第1袋和第3袋的组合去掉。注意我们不能枚举，我们得想办法把这个结果“算”出来。
实际上这个结果也不难算，包含第1袋的选法数目等于有几个袋子的金币与第3袋一样（包含2个金币的袋子数目）。你看(1, 3)(1, 4)(1, 5)实际上第3袋第4袋第5袋都是装着2个金币，与第3袋相同。同理包含第3袋的选法数目等于包含1个金币的袋子数目。(1, 3)(2, 3)实际上第1袋和第2袋都包含1个金币。多减了一次(1, 3).
于是我们需要多预处理一个结果：cnt1[X]表示包含X枚金币的袋子数量。
有了cnt2和cnt1，我们就可以进行计算了。当我们枚举分给小Hi的袋子是i=1和j=3时，分给小Ho的选法一共有：cnt2[A[i] + A[j]] – cnt1[A[i]] – cnt1[A[j]] + 1
注意这里+1是因为容斥原理，(1, 3)这个组合被减了2次。另外上面容斥原理算式还有个特例，就是A[i]等于A[j]的时候，这个时候小Ho的选法一共有：cnt2[A[i] + A[j]] – cnt1[A[i]] – cnt1[A[j]] + 3
举例：假设a[1]=2,a[2]=2,a[3]=2,a[4]=2; 那么cnt2[4]=6,即(1,2)(1,3)(1,4)(2,3)(2,4)(3,4), cnt1[2] = 4
当选i=1,j=2的时候，减去(cnt1[2]+cnt1[2]),即减去(1,1)(1,2)(1,3)(1,4)(2,1)(2,2)(2,3)(2,4)多减去了(1,1)(2,1)(2,2)这3个

#include 
#include 

题目链接:#1686 : 互补二元组
时间限制:10000ms
单点时限:1000ms
内存限制:256MB
描述
给定N个整数二元组(X1, Y1), (X2, Y2), … (XN, YN)。

请你计算其中有多少对二元组(Xi, Yi)和(Xj, Yj)满足Xi + Xj = Yi + Yj且i < j。

输入
第一行包含一个整数N。

以下N行每行两个整数Xi和Yi。

对于70%的数据，1 ≤ N ≤ 1000

对于100%的数据，1 ≤ N ≤ 100000 -1000000 ≤ Xi, Yi ≤ 1000000

输出
一个整数表示答案。

样例输入
5
9 10
1 3
5 5
5 4
8 6
样例输出
2

#include 
#include 

---

#枚举与优化套路（5）

双指针
我们来具体看一道题。
给定N个整数A1， A2， … ，AN，以及一个正整数K。问在所有的大于等于K的两个数的差(Ai-Aj)中，最小的差是多少。(N <= 100000)
那我们怎么用双指针优化呢？首先就是对A数组排序。比如假设排好序的A数组是：
A=[1, 3, 7, 8, 10, 15], K=3
这时我们枚举两个数中较小的是A[i]，较大的数是A[j]；对于A[i]来说，我们要找到最优的A[j]，也就是最小的A[j]满足A[j]-A[i]>=k

#include 
#include 
using namespace std;
int n, k, ans;
int a[100000];
int main(){
	cin >> n >> k;
	for(int i=0; i> a[i];
	}
	sort(a, a+n);
	if(a[n-1] - a[0] < k){
		cout << "no solution" << endl;
		return 0;
	}
	ans = a[n-1] - a[0];
	for(int i=0, j=0; i=k && a[j]-a[i]

题目链接:#1745 : 最大顺子
##1745 : 最大顺子
时间限制:10000ms
单点时限:1000ms
内存限制:256MB
描述
你有N张卡片，每张卡片上写着一个正整数Ai，并且N张卡片上的整数各不相同。

此外，你还有M张百搭卡片，可以当作写着任意正整数的卡片。

一个“顺子”包含K张卡片，并且满足卡片上的整数恰好是连续的K个正整数。我们将其中最大的整数称作顺子的值。

例如1-2-3-4-5的值是5，101-102-103的值是103。

请你计算用给定的N张卡片和M张百搭卡片，能凑出的值最大的顺子是多少，并且输出该顺子的值。

输入
第一行包含3个整数，N，M和K。

第二行包含N个整数，A1, A2, … AN。

对于50%的数据，1 ≤ N, K ≤ 1000

对于100%的数据，1 ≤ N, K ≤ 100000 0 ≤ M < K 0 ≤ Ai ≤ 100000000

输出
一个整数代表答案

样例输入
10 1 5
1 4 2 8 5 7 10 11 13 3
样例输出
11

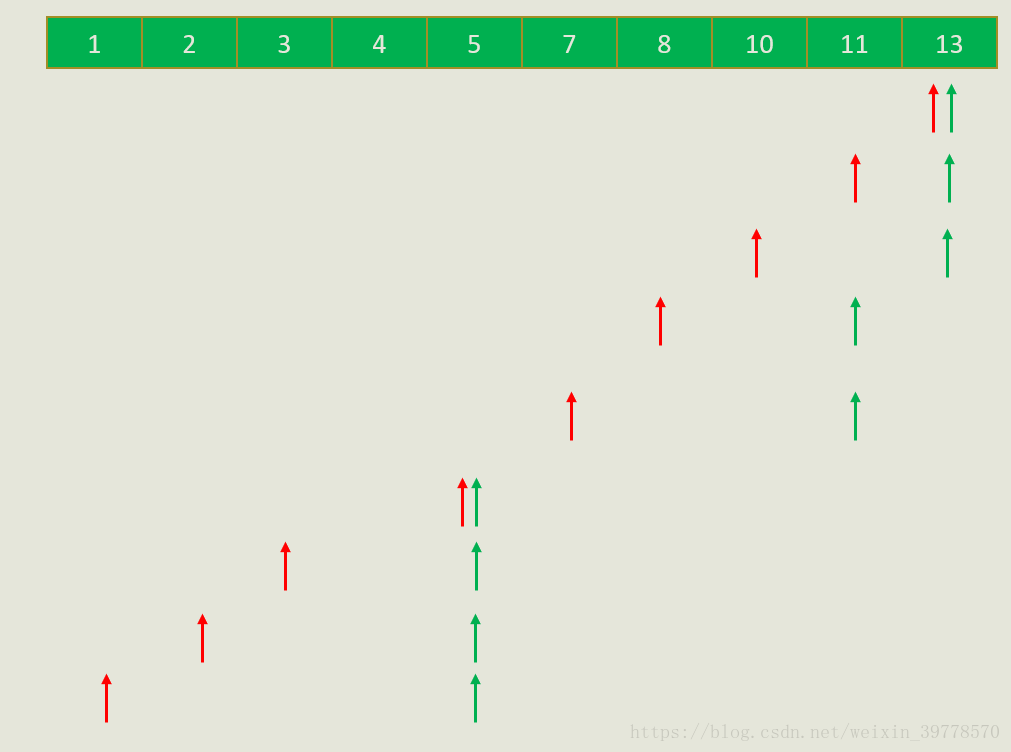
首先我们就是要对A数组排序，然后对于每一个A[i]，我们还是找到一个”最优的A[j]”。这里所谓“最优”是指最大的A[j]满足：A[i]~A[j]之间需要用百搭卡的整数不超过M张。
上图是样例每个Ai对应的最优的Aj，可以看出当A[i]从大到小枚举的过程中，A[j]也是从大到小改变，不会变大。所以这个双指针枚举的复杂度是O(N)的。
对于每个A[i]，当我们求出最优的A[j]之后，就可以计算以A[i]开头的顺子能不能凑出了。回顾一下我们定义“最优”的A[j]是指最大的A[j]满足：A[i]_{A[j]之间需要用百搭卡的整数不超过M张。而A[i]}A[j]一共需要的百搭卡是(A[j]-A[i])-(j-i)张，那么剩余的百搭卡一定是用在A[j]+1, A[j]+2…,我们只需要判断剩余的百搭卡是不是足够用到A[i]+K-1即可。

#include 
#include 
#include 
using namespace std;
int n, m, k;
vector a;
int main(){
	cin >> n >> m >> k;
	for(int i=0; i> x;
		a.push_back(x);
	}
	sort(a.begin(), a.end());
	int ans = -1;
	for(int i=n-1, j =n-1; i>=0; i--){
		int needed = a[j] - a[i] - (j-i); // 中间缺少的个数 
		while(needed > m){ // 当缺少个数超过万能卡的时候，右指针左移动 
			j--;
			needed = a[j] - a[i] - (j-i);
		}
		if(a[j] - a[i] + 1 + (m-needed) >= k){ // 找到顺子长度大于k 
			ans = a[j] + (m-needed);
			break;
		}
	}
	cout << ans << endl;
	return 0;
}

---

#枚举与优化套路（6）

双指针

题目连接:#1514 : 偶像的条件
##1514 : 偶像的条件
时间限制:10000ms
单点时限:1000ms
内存限制:256MB
描述
小Hi的学校正面临着废校的大危机。面对学校的危机，小Hi同学们决定从ABC三个班中各挑出一名同学成为偶像。

成为偶像团体的条件之一，就是3名团员之间的身高差越小越好。

已知ABC三个班同学的身高分别是A1…AN, B1…BM 和 C1…CL。请你从中选出3名同学Ai, Bj, Ck使得D=|Ai-Bj|+|Bj-Ck|+|Ck-Ai|最小。

输入
第一行包含3个整数，N, M和L。

第二行包含N个整数，A1, A2, … AN。(1 <= Ai <= 100000000)

第三行包含M个整数，B1, B2, … BM。(1 <= Bi <= 100000000)

第四行包含L个整数，C1, C2, … CL。(1 <= Ci <= 100000000)

对于30%的数据, 1 <= N, M, L <= 100

对于60%的数据，1 <= N, M, L <= 1000

对于100%的数据，1 <= N, M, L <= 100000

输出
输出最小的D。

样例输入
3 3 3
170 180 190
195 185 175
180 160 200
样例输出
10

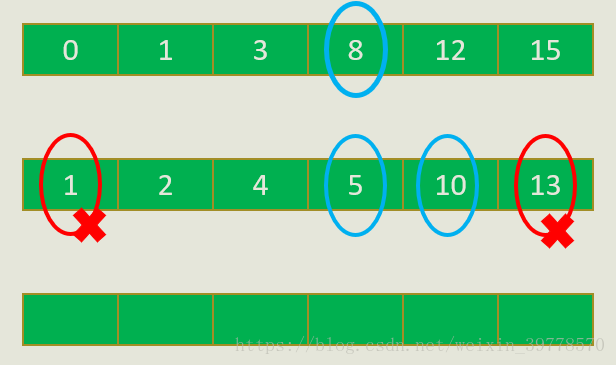
事实上可以证明：假设我们确定从第一个数组里选的是A[i]，那么第二个数组里选出的数一定是“小于等于A[i]的数里最大的”和”大于等于A[i]的数里最小的”二选一。例如在上图的例子里，我们假设从第一个数组挑了8，那么我们在第二个数组中只用考虑5和10，小于5的数一定不会比5更优，大于10的数一定不会比10更优。

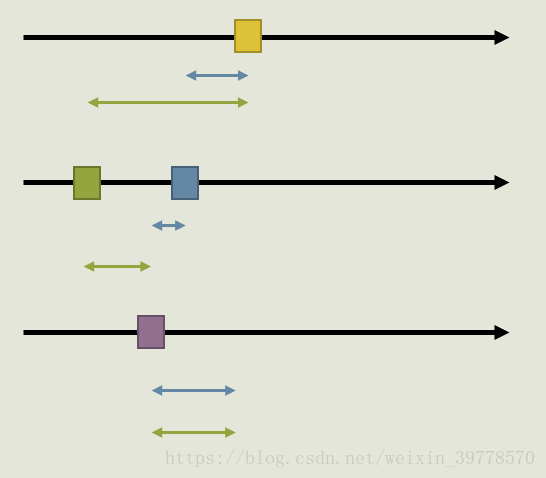
我们看一下上面这个图，三条黑色水平线是3个数轴，代表3个数组。数轴上的方块代表相应数组中的一个数。并且方块越靠右，代表数越大。我们假设确定从A数组中挑出的黄色方块这个数。我们现在要证明无论从C数组中挑出哪个，B数组中蓝色的方块一定比绿色的方块更优。
假设从C数组中挑选的数是紫色方块，在绿色方块右边，比绿色方块大。这时选蓝色方块时，3个数的差是3段蓝色的区间。选绿色方块时，3个数的差是3段绿色的区间。显然蓝色长度之和小于绿色长度之和。
我们再看下图，是另一种情况。假设C数组中挑选的数在绿色方块左边。

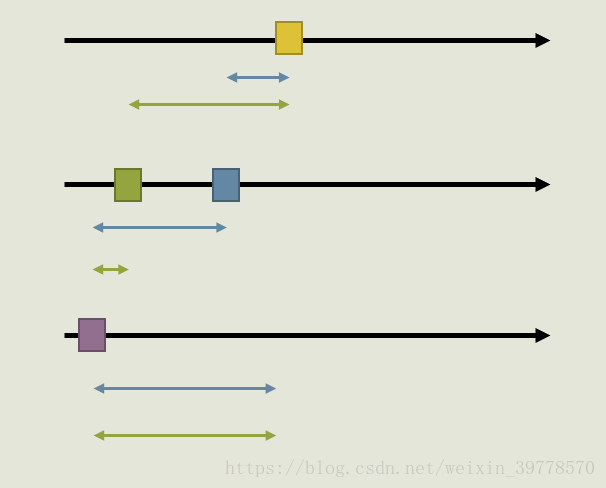
这时可以看到蓝色区间长度之和与绿色区间长度之和相等。所以综合以上两种情况，选绿色一定不比选蓝色优。证明了我们先前的结论。
有了这个结论我们就可以使用双指针的思路了。首先我们把3个数组都排序。然后依次枚举A数组中的一个数A[i]，表示我们从A数组中挑出的是A[i]。这时，我们求出B数组的一个下标j，满足B[j-1] <= A[i] <= B[j]，再求出来C数组的一个下标k，满足C[k-1] <= A[i] <= C[k]。我们知道包含A[i]的最优解一定在B[j-1]和B[j]二选一，C[k-1]和C[k]二选一，总共4种情况：{A[i], B[j-1], C[k-1]}, {A[i], B[j-1], C[k]},{A[i], B[j], C[k-1]},{A[i], B[j], C[k]}。

#include 
#include 
using namespace std;
int n, m, l;
int a[100010], b[100010], c[100010];	
long long ans;
void test(long long x, long long y, long long z){
	long long d = abs(x-y) + abs(z-x) + abs(y-z);
	if(d < ans) ans = d;
}
int main(){
	cin >> n >> m >> l;
	for(int i=1; i<=n; i++){
		cin >> a[i];
	}
	for(int i=1; i<=m; i++){
		cin >> b[i];
	}
	for(int i=1; i<=l; i++){
		cin >> c[i];
	}	
	a[0] = b[0] = c[0] = -1000000000;
	a[n+1] = b[m+1] = c[l+1] = 1000000000;
	sort(a, a+n+1);
	sort(b, b+m+1);
	sort(c, c+l+1);
	ans = 10000000000LL;
	for(int i=1, j=0, k=0; i<=n; i++){
		while(b[j+1] < a[i]) j++;
		while(c[k+1] < a[i]) k++;
		test(a[i], b[j], c[k]);
		test(a[i], b[j+1], c[k]);
		test(a[i], b[j], c[k+1]);
		test(a[i], b[j+1], c[k+1]);
	}
	cout << ans << endl;
	return 0;
}

题目链接:#1607 : H星人社交网络
##1607 : H星人社交网络
时间限制:10000ms
单点时限:1000ms
内存限制:256MB
描述
Handbook是H星人的一家社交网络。Handbook中共有N名用户，其中第i名用户的年龄是Ai。

根据H星人的文化传统，用户i不会给用户j发送好友请求当且仅当：

1. Aj < 1/8 * Ai + 8 或者

2. Aj > 8 * Ai + 8 或者

3. Ai < 88888 且 Aj > 88888

其他情况用户i都会给用户j发送好友请求。

你能求出Handbook总计会有多少好友请求吗？

输入
第一行一个整数N。

第二行N个整数A1, A2, … AN。

对于30%的数据，1 ≤ N ≤ 100

对于100%的数据，1 ≤ N ≤ 100000, 1 ≤ Ai ≤ 100000

输出
输出Handbook中好友请求的总数

样例输入
2
10 80
样例输出
1

我们优化的思路也和之前的一样，就是能不能只枚举Ai，而将符合条件的Aj数量直接”算”出来，而不是枚举出来。其实我们稍微分析一下题目的三个条件，就能看出来对于确定的Ai来说，他发好友请求的Aj一定是在某一个年龄区间的。
比如假设Ai=8，那么年龄在[9, 72]闭区间的用户都会被发好友请求。并且随着Ai增大，这个年龄区间也是逐渐向右移动的。向右移动是指区间的左端点和右端点都是向右移动的，不会减小。

#include 
#include 
using namespace std;
int n;
int a[100010];
int main(){
	cin >> n;
	for(int i=0; i> a[i];
	}
	sort(a, a+n);
	long long ans = 0;
	int l=0, r=-1;
	for(int i=0; i88888))) l++; //从不可以一直向右枚举到第一个可以
		while(r+1=88888 || a[r+1]<=88888)) r++; // 从可以一直向右枚举到第一个不可以 
		if(l <= r){
			ans += (r-l+1);
			if(l<=i && i<=r) ans--;
		}
	}
	cout << ans << endl;
	return 0;	
}

---

#枚举与优化套路（7）

前缀和

计算前缀和S[0], S[1], S[2], … S[N]。统计S[]中模K余0, 1, 2 … K-1的数量，记为cnt[0], cnt[1], cnt[2] … cnt[K-1]。答案就是：cnt[0](cnt[0]-1)/2 + cnt[1](cnt[1]-1)/2 +… +cnt[K-1]*(cnt[K-1]-1)/2。

#include 
#include 

#include 
#include 

---

#枚举与优化套路（8）

前缀和优化

题目链接:#1534 : Array Partition







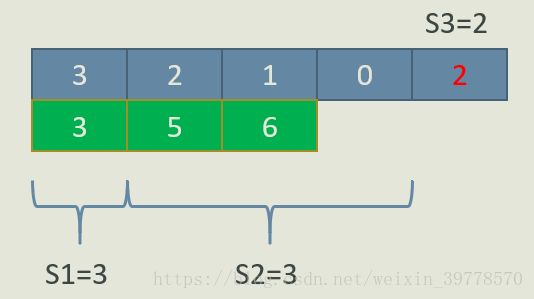
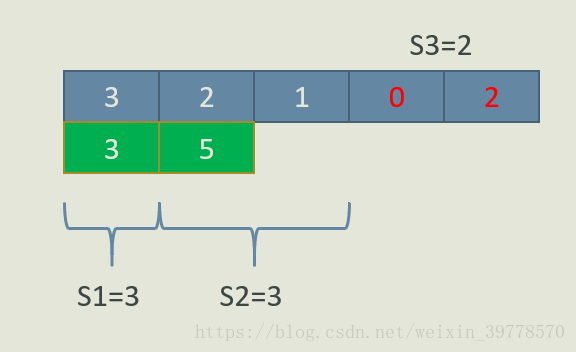
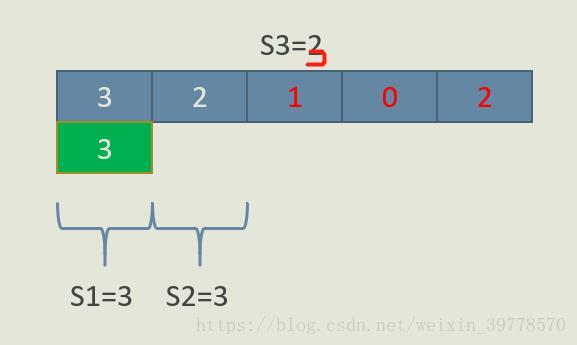
上面我们就把样例的3种划分方法都求出来了。我们回顾一下上面的思路，基本就是从N-1到2枚举q，对于每一个q，我们都要求一类问题的解：
q = N-1时，前缀和S[1], S[2], … S[N-2]中有几个前缀和的值是X？（这里X可能是S3-1， S3， S3+1）
q = N-2时，前缀和S[1], S[2], … S[N-3]中有几个前缀和的值是X？（这里X可能是S3-1， S3， S3+1）
…
q = 2时，前缀和S[1]中有几个前缀和的值是X？（这里X可能是S3-1， S3， S3+1）

对于这一类问题，就是一堆前缀和中，有几个X，我们当然可以用哈希表来实现。使得每次询问的复杂度都是O(1)的。具体来说，我们可以用unordered_map cnt来保存每个值出现了几次，例如cnt[3]表示前缀和是3的有几个。注意这里key的类型是long long，因为前缀和可能超过int范围。

/*#1534 : Array Partition*/
#include 
#include 

第18行是在枚举q，也就是最后一段的断点。第19行是计算q对应的s3，因为随着q减少，第三段的和是增加的。注意第20行很关键，cnt[s[q]]–实际上就是把s[q]剔除出哈希表。这是我们之前提到的，随着q减少，我们关心的前缀和集合也在变短，q=N-1的时候我们关心s[0]~s[N-2]，q=2的时候我们就只关心s[1]一个前缀和了。所以这里是把我们不关心的去掉。

第21行是在枚举S1可能的取值，也就是S3-1, S3, S3+1。第22行是在计算S2的值。第23行是在判断S2的值符不符合要求，也就是S1成不成立。如果成立，那么cnt中有几个前缀和的值是S1，就有几个合法的划分方案。于是我们给答案ans累加上cnt[s1]。