AVL树详解（可视化工具）

转自：AVL树(一)之 图文解析 和 C语言的实现（本文图片及文字描述部分转自该文）
参考：邓俊辉 的数据结构，部分图片来自该资料

代码是C#写的

AVL树是根据它的发明者G.M. Adelson-Velsky和E.M. Landis命名的。
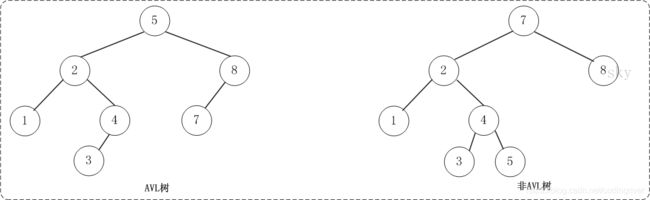
它是最先发明的自平衡二叉查找树，也被称为高度平衡树。相比于"二叉查找树"，它的特点是：AVL树中任何节点的两个子树的高度最大差别为1。(树的高度：树中结点的最大层次)

上面的两张图片，左边的是AVL树，它的任何节点的两个子树的高度差别都<=1；而右边的不是AVL树，因为7的两颗子树的高度相差为2(以2为根节点的树的高度是3，而节点8的高度是1)。

AVL树的查找、插入和删除在平均和最坏情况下都是O(logn)。
如果在AVL树中插入或删除节点后，使得高度之差大于1。此时，AVL树的平衡状态就被破坏，它就不再是一棵二叉树；为了让它重新维持在一个平衡状态，就需要对其进行旋转处理。学AVL树，重点的地方也就是它的旋转算法

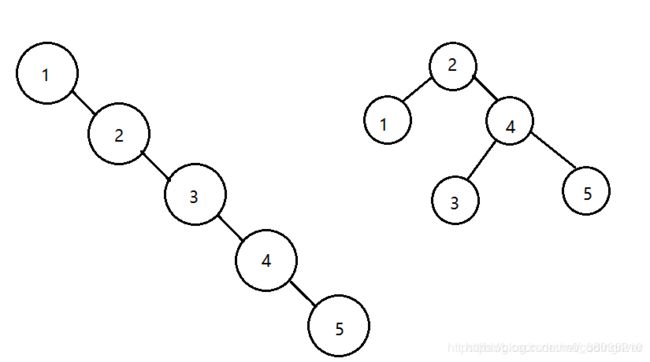
首先要明确的是，== 平衡二叉树是一棵二叉排序树，它的出现是为了解决普通二叉排序树（普通二叉排序树）不平衡的问题。如图，在插入结点之前首先要查找插入位置，假如要在5结点后插入，普通二叉排序树需要比较五次，而平衡二叉树只需要比较三次。假如结点规模进一步加大，效率提升也会更明显。
(图片来自https://blog.csdn.net/m0_38036210/article/details/100517125)

0X01 节点和树的定义

1. 节点的定义

    public class Node
    {
        public int Key;
        public Node Parent;//parent
        public Node L; //left
        public Node R; //right
        public int H; //height;

        public Node(int key, Node parent=null, Node left=null, Node right=null,int h=1)
        {
            Key = key;
            Parent = parent;
            L = left;
            R = right;
            H = h;
        }

	}

2. 树的定义

    public class AVLTree
    {
        //树的根节点
        public Node Root;
	}

3.树的高度

空的二叉树的高度是0，非空树只有一个节点根节点高度为1等等

        /// 

        /// 树的高度
        /// 树的高度为最大层次。即空的二叉树的高度是0，非空树的高度等于它的最大层次(根的层次为1，根的子节点为第2层，依次类推)，这里空树的高度取0，有的教材资料是-1
        /// 
        /// 
        /// 
        public int Height(Node a)
        {
            return a == null ? 0 : a.H;
        }

        public int MaxHeight(Node a, Node b)
        {
            return a == null ? (b == null ? 0 : b.H) : (b == null ? a.H : a.H > b.H ? a.H : b.H);
        }

        public int UpdateHeight(Node a)
        {
            a.H = MaxHeight(a.L, a.R) + 1;
            return a.H;
        }      
        /// 

        /// 是否平衡
        /// 
        /// 
        /// 
        public bool IsBalanced(Node tree)
        {
            return -2 < Height(tree.L) - Height(tree.R) && Height(tree.L) - Height(tree.R) < 2;
        }   
        /// 

        /// 在左、右孩子中取更高者
        /// 
        /// 
        /// 
        public Node TallerChild(Node tree)
        {
            if (tree == null)
                return null;
            if (Height(tree.L) > Height(tree.R))
                return tree.L;
            else return tree.R;
        }             

0X02 单旋和双旋

前面说过，如果在AVL树中进行插入或删除节点后，可能导致AVL树失去平衡。

2.1 zag单旋（左旋）

如果说节点g失去平衡，g的右孩子p高度比左孩子高，且右孩子p的右孩子v高度比右孩子p的左孩子高度高，那么进行逆时针旋转进行调整高度

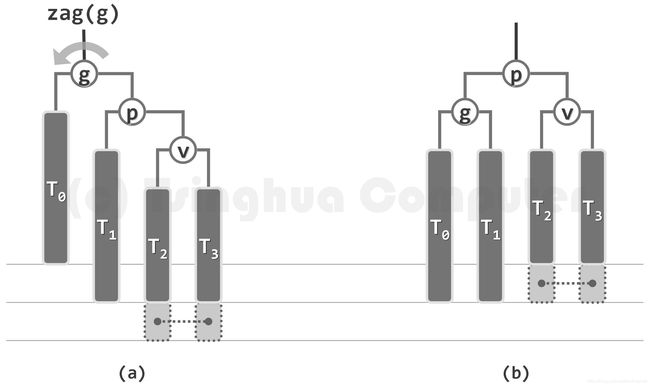
假设在子树v中插入某个节点x（虚线连接部分，其中一个节点对应x，另一个为空节点），这时候v节点是平衡的，p节点也是平衡，但是g节点不平衡，g的右孩子高度减去g的做孩子高度等于2，需要对g节点进行调整，这时候以g为轴进行逆时针旋转（左旋），调整后从a子树变为b子树；从而达到子树的平衡， 而且高度未变化，所以该子树平衡后，父节点及除子树的其他树的部分都是平衡的。

旋转代码

         /// 

        /// zag 左旋转，逆时针旋转,单旋       
        ///   （逆时针旋转g）  
        ///         g          
        ///        / \         
        ///       T0  p        
        ///          / \       
        ///         T1  v      
        ///            / \     
        ///           T2  T3   
        /// 
        ///     zag单旋后：    
        ///         p(b)         
        ///       /     \      
        ///      g(a)    v(c)     
        ///     / \     / \    
        ///    T0  T1  T2  T3  
        /// 
        /// 
        /// 非空孙辈节点
        /// 该树新的的根节点
        public Node Zag(Node tree)
        {
            Node v = tree, p = v.Parent, g = p.Parent, r = g.Parent;
            Node a = g, b = p, c = v;
            Node T0 = g.L, T1 = p.L, T2 = v.L, T3 = v.R;
            a.L = T0; if (T0 != null) T0.Parent = a;
            a.R = T1; if (T1 != null) T1.Parent = a; UpdateHeight(a);
            c.L = T2; if (T2 != null) T2.Parent = c;
            c.R = T3; if (T3 != null) T3.Parent = c; UpdateHeight(c);
            b.L = a; a.Parent = b;
            b.R = c; c.Parent = b; UpdateHeight(b);
            Connect(r, b); //根节点和父节点联接
            return b;//该树新的的根节点
        }

2.2 zig单旋（右旋）

假设在子树v中插入某个节点x（虚线连接部分，其中一个节点对应x，另一个为空节点），这时候v节点是平衡的，p节点也是平衡，但是g节点不平衡，g的右孩子高度减去g的做孩子高度等于-2，需要对g节点进行调整，这时候以g为轴进行顺时针旋转（右旋），调整后从a子树变为b子树；从而达到子树的平衡， 而且高度未变化，所以该子树平衡后，父节点及除子树的其他树的部分都是平衡的。

旋转代码

        /// 

        /// Zig右旋，顺时针旋转,单旋
        ///    （顺时针旋转g）
        ///           g       
        ///          / \      
        ///         p   T3    
        ///        / \        
        ///       v   T2      
        ///      / \          
        ///     T0  T1        
        /// 
        ///   zig单旋后：     
        ///         p(b)        
        ///       /     \     
        ///      v(a)    g(c)    
        ///     / \     / \   
        ///    T0  T1  T2  T3 
        /// 
        /// 
        /// 非空孙辈节点
        /// 该树新的的根节点
        public Node Zig(Node tree)
        {
            Node v = tree, p = v.Parent, g = p.Parent, r = g.Parent;
            Node a = v, b = p, c = g;
            Node T0 = v.L, T1 = v.R, T2 = p.R, T3 = g.R;
            a.L = T0; if (T0 != null) T0.Parent = a;
            a.R = T1; if (T1 != null) T1.Parent = a; UpdateHeight(a);
            c.L = T2; if (T2 != null) T2.Parent = c;
            c.R = T3; if (T3 != null) T3.Parent = c; UpdateHeight(c);
            b.L = a; a.Parent = b;
            b.R = c; c.Parent = b; UpdateHeight(b);

            Connect(r, b); //根节点和父节点联接
            return b;//该树新的的根节点
        }

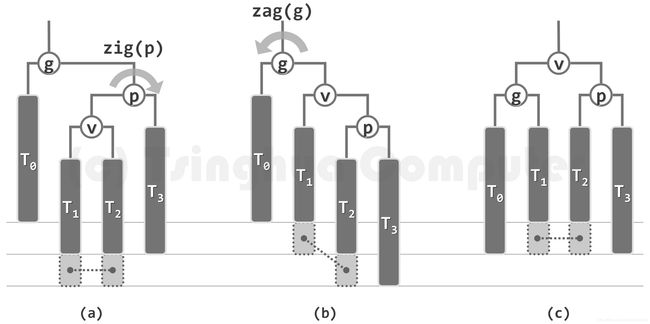
2.3 zagzig双旋

（先逆时针旋转p(zag)，后顺时针旋转g(zig)）

旋转代码

        /// 

        /// ZagZig 双旋(先左旋p后右旋g)
        ///  
        ///  （先逆时针旋转p(zag)，后顺时针旋转g(zig)）
        ///                      g                     
        ///                     / \                    
        ///                    p   T3                  
        ///                   / \                      
        ///                  T0  v                     
        ///                     / \                    
        ///                    T1  T2                  
        /// 
        ///                zag-zig双旋后               
        ///                     v(b)                    
        ///                   /     \                  
        ///                  p(a)    g(c)                 
        ///                 / \     / \                
        ///                T0  T1  T2  T3              
        ///                
        /// 
        /// 非空孙辈节点
        /// 该树新的的根节点
        public Node ZagZig(Node tree)
        {
            Node v = tree, p = v.Parent, g = p.Parent, r = g.Parent;
            Node a = p, b = v, c = g;
            Node T0 = p.L, T1 = v.L, T2 = v.R, T3 = g.R;
            a.L = T0; if (T0 != null) T0.Parent = a;
            a.R = T1; if (T1 != null) T1.Parent = a; UpdateHeight(a);
            c.L = T2; if (T2 != null) T2.Parent = c;
            c.R = T3; if (T3 != null) T3.Parent = c; UpdateHeight(c);
            b.L = a; a.Parent = b;
            b.R = c; c.Parent = b; UpdateHeight(b);
            Connect(r, b); //根节点和父节点联接
            return b;//该树新的的根节点
        }

2.4 zigzag双旋

先顺时针旋转p(zig)，后逆时针旋转g(zag)

旋转代码

        /// 

        /// ZigZag 双旋（先右旋p后左旋g）
        ///（先顺时针旋转p(zig)，后逆时针旋转g(zag)）
        ///                    g       
        ///                   / \      
        ///                 T0   p     
        ///                     / \    
        ///                    v   T3  
        ///                   / \      
        ///                  T1  T2    
        ///        
        ///               zig-zag双旋后
        ///                   v(b)      
        ///                 /     \    
        ///                g(a)    p(c)   
        ///               / \     / \  
        ///              T0  T1  T2  T3
        ///                     
        /// 
        /// 非空孙辈节点
        /// 该树新的的根节点
        public Node ZigZag(Node tree)
        {
            Node v = tree, p = v.Parent, g = p.Parent, r = g.Parent;
            Node a = g, b = v, c = p;
            Node T0 = g.L, T1 = v.L, T2 = v.R, T3 = p.R;
            a.L = T0; if (T0 != null) T0.Parent = a;
            a.R = T1; if (T1 != null) T1.Parent = a; UpdateHeight(a);
            c.L = T2; if (T2 != null) T2.Parent = c;
            c.R = T3; if (T3 != null) T3.Parent = c; UpdateHeight(c);
            b.L = a; a.Parent = b;
            b.R = c; c.Parent = b; UpdateHeight(b);
            Connect(r, b); //根节点和父节点联接
            return b;//该树新的的根节点
        }

0X03 查找

        /// 

        /// 查找
        /// 
        /// 
        /// 
        /// 
        public Node Search(Node tree,int key)
        {
            return SearchIn(tree, key, out _);
        }

        /// 

        /// 查找键值key的节点并且返回（key对应节点为命中节点）
        /// 
        /// 子树
        /// 查找键值
        /// 返回命中节点的父节点，如果不存在命中节点则返回预判命中节点的父节点；（当命中节点为tree时，hot为NULL）
        /// 命中节点
        public Node SearchIn(Node tree, int key, out Node hot)
        {
            // hot :如果没有命中节点，则hot命中后做多只有一个节点，且key是对应另外一个孩子空节点位置

            Node n = tree;
            if (tree == key) //在子树根节点tree处命中
            {
                hot = null;
                return tree;
            }

            for (; ; )
            {
                hot = n;
                n = n > key ? n.L : n.R;
                if (n == null || n == key) return n; //返回命中节点，hot指向父节点，hot必然命中（在key不存在时,n==null）
            }
        }

0X04 插入

插入节点的代码

        public Node Insert(int key)
        {
            Console.WriteLine($"Insert:{key}"); //打印日志
            Node n = Insert(Root, key);
            PrintTree(Root);//打印日志 打印树
            return n;
        }
        public Node Insert(Node tree, int key)
        {
            if (Root == null)
                return Root = CreateNode(key);

            Node hot;
            Node x = SearchIn(tree, key, out hot);
            if (x != null) return x;
            x = CreateNode(key, hot); //hot最多只有一个节点

            for (Node n = hot; n != null; n = n.Parent) // //从x之父出发向上，逐层检查各代祖先g
            {
                if (!IsBalanced(n)) //一旦发现g失衡，则（采用“3 + 4”算法）使之复衡，并将子树
                {
                    RotateAt(n);
                    break; //g复衡后，局部子树高度必然复原；其祖先亦必如此，故调整随即结束
                }
                else  //否则（g依然平衡），只需简单地
                    UpdateHeight(n); //更新其高度（注意：即便g未失衡，高度亦可能增加）
            } // 至多只需一次调整；若果真做过调整，则全树高度必然复原
            return x; //返回新节点位置

        }

0X05 删除

删除节点的代码

        /// 

        /// 删除节点
        /// 
        /// 
        /// 
        Node Remove(int key)
        {
            Console.WriteLine($"Remove:{key}"); //打印日志
            Node n = Remove(Root, key);
            PrintTree(Root);//打印日志 打印树
            return n;
        }
        Node Remove(Node tree,int key)
        {
            Node hot;
            Node x = SearchIn(tree, key, out hot);
            x = RemoveAt(x, out hot);

            for (Node n = hot; n != null; n = n.Parent) // //从x之父出发向上，逐层检查各代祖先g
            {
                if (!IsBalanced(n)) //一旦发现g失衡，则（采用“3 + 4”算法）使之复衡，并将子树
                {
                    RotateAt(n);
                    break; //g复衡后，局部子树高度必然复原；其祖先亦必如此，故调整随即结束
                }
                else  //否则（g依然平衡），只需简单地
                    UpdateHeight(n); //更新其高度（注意：即便g未失衡，高度亦可能增加）
            } // 至多只需一次调整；若果真做过调整，则全树高度必然复原
            return x;
        }


        Node RemoveAt(Node x,out Node hot)
        {
            if (x == null)
            {
                hot = null;
                return null;
            }
                
            Node succ=null;
            Node parent = x.Parent;
            if (!HasLeft(x))
                succ = x.R;
            else if (!HasRight(x))
                succ = x.L;
            else
            {
                succ = Successor(x);
                SwapData(x, succ);
                x = succ;
                succ = x.R; //succ = Successor(x) 这行执行前，succ是x的后继，而且succ是x右子树中的一个节点，所以succ是没有左孩子的，可能有右孩子，那么succ的后继只能是succ.Parent，继succ=x.Parent
                parent = x.Parent;                
            }

            if (IsLeft(x)) x.Parent.L = null; //断开父节点的连接
            else if (IsRight(x)) x.Parent.R = null; //断开父节点的连接            
            Connect(parent, succ);
            hot = parent;
            x.L = x.R = x.Parent = null; //clean
            
            return x;
        }

0X07 打印二叉树代码（C#）

        public void Print(Node node)
        {
            Console.Write($"{node.Key},");
        }
        /// 

        /// 打印二叉树 打印数值最大3位数
        /// 
        /// 树的根节点
        public static void PrintTree(Node tree)
        {
            System.Text.StringBuilder builder = new System.Text.StringBuilder();
            PrintTree(tree, builder);
            Console.WriteLine(builder.ToString());
        }
        
        static void PrintTree(Node tree,System.Text.StringBuilder builder)
        {
            List<List<Node>> list = new List<List<Node>>();
            Queue<Node> queue = new Queue<Node>();
            Queue<Node> queue1 = null;
            queue.Enqueue(tree);
            while(queue.Count>0)
            {
                List<Node> levels = new List<Node>();
                queue1 = new Queue<Node>();
                int nullCount = 0;
                while (queue.Count>0)
                {
                    Node n = queue.Dequeue();
                    Node l=n!=null?n.L:null, r= n != null ? n.R : null;
                    
                    levels.Add(n);
                    queue1.Enqueue(l);
                    queue1.Enqueue(r); 
                    nullCount += l == null ? 1 : 0;
                    nullCount += r == null ? 1 : 0;
                }
                queue = queue1;
                list.Add(levels);
                if(queue.Count==nullCount)
                {
                    break;
                }
            }


            int level = list.Count;
            int maxLevelNodeCount = GetMaxNodeCountByDepth(level);
            int space=0;

            for (int i = level-1; i >=0; i--)
            {
                System.Text.StringBuilder sb = new System.Text.StringBuilder();
                System.Text.StringBuilder top = new System.Text.StringBuilder();
                int space1 = space;
                space = space * 2 + 1;
                for (int s = 0; s < space1; s++)
                {
                    sb.Append("   ");
                    top.Append("   ");
                }
                List<Node> ls = list[i];
                for (int k = 0; k < ls.Count; k++)
                {
                    string v = ls[k] == null ? " N " : ls[k].Key.ToString("D3");
                    sb.Append($"{v}");
                    top.Append("/ \\");
                    for (int j = 0; j < space; j++)
                    {
                        sb.Append($"   ");
                        top.Append($"   ");
                    }
                }
                
                top.Append("\n");
                sb.Append("\n");
                
                if (i!=level-1)
                    builder.Insert(0, top.ToString());
                builder.Insert(0, sb.ToString());


            }
        }

打印结果：
打印数值最大3位数

0X07 完整代码（C#）

完整代码(github)

0X08 AVL树测试

测试完整代码(github)和完整代码一样
测试插入和删除。测试中对zig、zag、zigzag、zagzig操作在插入时都执行了；删除操作执行了部分操作，剩余可以自己完善测试案例，
测试代码

       static void Main1()
       {
           AVLTree tree = new AVLTree();
           Node n,n1,n2;
           tree.Insert(20);
           tree.Insert(10);
           tree.Insert(7);  /* 执行zig （插入节点后右旋20）*/
           tree.Insert(24);
           tree.Insert(26); /* 执行zag （插入节点后左旋20）*/
           tree.Insert(12); /* 执行zig-zag （插入节点后先右旋24后左旋10）*/
           tree.Insert(14); 
           tree.Insert(16); /* 执行zag （插入节点后左旋12）*/
           tree.Insert(13); /* 执行zig-zag （插入节点后先右旋14后左旋10）*/
           tree.Insert(17); /* 执行zag-zig （插入节点后先左旋12后右旋20）*/
           tree.Insert(18);  /* 执行zag （插入节点后左旋16）*/
           Console.Write("   Preorder::");
           tree.Preorder(tree.Root);
           Console.WriteLine();
           Console.Write("    Inorder::");
           tree.Inorder(tree.Root);
           Console.WriteLine();
           Console.Write("  Postorder::");
           tree.Postorder(tree.Root);
           Console.WriteLine();
           Console.Write(" Levelorder::");
           tree.Levelorder(tree.Root);
           Console.WriteLine();
           Console.Write(" ZLevelorder:");
           tree.ZLevelorder(tree.Root);
           Console.WriteLine("\n\n");

           tree.Remove(14);
           tree.Remove(12);/* 执行zig （删除节点后右旋13）*/
           tree.Remove(10);
           tree.Remove(7); /* 执行zag （删除节点后左旋16）*/
           tree.Remove(26);/* 执行zag-zig （删除节点后先左旋16后右旋20）*/
           tree.Remove(17);
           tree.Remove(18);

           Console.ReadKey();
       }

测试结果

Insert:20
020

Insert:10
   020
   / \
010    N

Insert:7
   010
   / \
007   020

Insert:24
         010
         / \
   007         020
   / \         / \
 N     N     N    024

Insert:26
         010
         / \
   007         024
   / \         / \
 N     N    020   026

Insert:12
         020
         / \
   010         024
   / \         / \
007   012    N    026

Insert:14
                     020
                     / \
         010                     024
         / \                     / \
   007         012          N          026
   / \         / \         / \         / \
 N     N     N    014    N     N     N     N

Insert:16
                     020
                     / \
         010                     024
         / \                     / \
   007         014          N          026
   / \         / \         / \         / \
 N     N    012   016    N     N     N     N

Insert:13
                     020
                     / \
         012                     024
         / \                     / \
   010         014          N          026
   / \         / \         / \         / \
007    N    013   016    N     N     N     N

Insert:17
                     014
                     / \
         012                     020
         / \                     / \
   010         013         016         024
   / \         / \         / \         / \
007    N     N     N     N    017    N    026

Insert:18
                     014
                     / \
         012                     020
         / \                     / \
   010         013         017         024
   / \         / \         / \         / \
007    N     N     N    016   018    N    026

   Preorder::14,12,10,7,13,20,17,16,18,24,26,
    Inorder::7,10,12,13,14,16,17,18,20,24,26,
  Postorder::7,10,13,12,16,18,17,26,24,20,14,
 Levelorder::14,12,20,10,13,17,24,7,16,18,26,
 ZLevelorder:14,20,12,10,13,17,24,26,18,16,7,


Remove:14
                     016
                     / \
         012                     020
         / \                     / \
   010         013         017         024
   / \         / \         / \         / \
007    N     N     N     N    018    N    026

Remove:12
                     016
                     / \
         010                     020
         / \                     / \
   007         013         017         024
   / \         / \         / \         / \
 N     N     N     N     N    018    N    026

Remove:10
                     016
                     / \
         013                     020
         / \                     / \
   007          N          017         024
   / \         / \         / \         / \
 N     N     N     N     N    018    N    026

Remove:7
                     020
                     / \
         016                     024
         / \                     / \
   013         017          N          026
   / \         / \         / \         / \
 N     N     N    018    N     N     N     N

Remove:26
         017
         / \
   016         020
   / \         / \
013    N    018   024

Remove:17
         018
         / \
   016         020
   / \         / \
013    N     N    024

0X09 AVL树可视化工具

AVL树可视化工具（旧金山大学 (usfca)|数据结构可视化工具）