《算法导论》红黑树详解（一）：概念

在学习红黑树之前，读者应先掌握二叉查找树的相关知识。学习红黑树或者二叉查找树，推荐大家看《算法导论》。《算法导论》原书第3版 高清PDF 带详细书签目录下载 密码：acis

《算法导论》红黑树详解（一）：概念
《算法导论》红黑树详解（二）：Java实现Demo

一、红黑树介绍

  红黑树是每个结点都带有颜色属性的二叉查找树，颜色为红色或黑色。通过对任意一条从根到叶子的简单路径上各个结点的颜色进行约束，红黑树确保没有一条路径比其他路径长2倍，因而是近似于平衡的。

  树中每个结点包含5个属性：color、key、left、right和p（父结点），如果一个结点缺少子结点或父结点，则缺少的结点用NIL结点代替，NIL是一个黑色结点，它不包含数据而只充当树在此结束的指示。

​ 红黑树作为一颗二叉查找树的同时，必须具备如下5个性质，即红黑性质：

​ 1. 每个结点的颜色为红色或者黑色。

​ 2. 根结点是黑色的。

​ 3. 每个叶结点是黑色的（叶结点是指NIL结点）。

​ 4. 如果一个结点是红色的，则它的两个子结点都是黑色的。（树中不存在两个连续的红色结点）。

​ 5. 对任意结点，从该结点到其后代叶结点的简单路径上，均包含相同数目的黑色结点。

下面是一个具体的红黑树的图例：

  正是这些性质保证了红黑树的关键特性：对任意结点，从该结点的到其后代叶结点的最长的可能路径不多于最短的可能路径的2倍。 证明：最长的路径由红、黑结点相间组成，最短的路径全都由黑色结点组成，由于黑色结点数目相同，那么最长路径不会超过最短路径两倍。这个特性使红黑树大致上是平衡的，而平衡二叉树可以极大地缩短查找时所消耗的时间，这也是红黑树存在的意义。

  为了便于处理红黑树代码中的边界条件和节省空间，使用一个哨兵T.nil来代替NIL，并且根结点的父节点也指向T.nil，如下图。为了更加直观，在后面的图例中并不会画出T.nil。

二、旋转

  在讲红黑树插入和删除之前，先要了解旋转操作，因为插入和删除可能会破坏红黑树的性质，我们必须通过对结点进行变色和旋转来维护红黑树的性质。

​  旋转分为两种：左旋和右旋，见下图。左旋和右旋是相对称的操作，因此这里就左旋进行介绍：假设x和y都是不为T.nil的结点，且y为x的右孩子，现在对结点x进行左旋，以x与y的连线为轴向左旋转，使y成为该子树新的根结点，x成为y的左孩子，y的左孩子成为x的右孩子。

左旋的伪代码（参考自《算法导论》）：

LEFT-ROTATE(T,x)
    y = x.right              // y为x的右孩子
    x.right = y.left         // x抛弃他的右孩子，去认y的左孩子为他的右孩子，但这个孩子(T.nil除外)并没有认这个爹，所以有了下一步的认爹操作
    if y.left != T.nil
        y.left.p = x         // y的左孩子认x这个爹
    y.p = x.p                // y抛弃他以前的爹，认x的爹为爹，但x的爹还没有认这个孩子，下面就是认孩子操作
    if x.p == T.nil          // 若x没有爹
        T.root = y           // 则y成为祖先
    else if x == x.p.left    // 否则，即x有爹，如果x作为左孩子
        x.p.left = y         // x的爹抛弃x,认y为左孩子
    else
        x.p.right = y        // 如果x作为右孩子，认y为右孩子
    y.left = x               // y认x为左孩子
    x.p = y                  // x认y为爹

给出一个《算法导论》上的实例：

三、插入

红黑树的插入与二叉查找树的类似，原理是一样的。我们先来复习一下二叉查找树的插入操作。

二叉查找树插入伪代码（参考自《算法导论》）：

TREE-INSERT(T,z)
    y = NIL               // y用来记录z的父结点
    x = T.root
    while x != NIL        // 迭代查找出z的父结点，用y记录
        y = x
        if z.key < x.key
            x = x.left
        else
            x = x.right
    z.p = y               // z的父结点为y
    if y == NIL
        T.root = z        // y为空(NIL)，则z为根结点
    else if z.key < y.key
        y.left = z        // z小于y，则z为y的左孩子
    else
        y.right = z       // z大于y，则z为y的右孩子

看下面一个实例，将15插入到二叉查找树中，红线为迭代过程。

红黑树插入过程：先将红黑树当作二叉查找树，将结点插入，然后将插入的结点着为红色，最后通过一系列的重新着色和旋转操作，使树恢复红黑性质。

解释一下为什么着为红色：因为着为红色没有破坏性质5，但可能破坏性质4，而着为黑色一定破坏了性质5，破坏了性质5修复起来较困难，所以我们选择将插入结点着为红色。

红黑树插入伪代码（参考自《算法导论》）：

RB-INSERT(T, z)
    y = T.nil               // y用来记录z的父结点
    x = T.root
    while x != T.nil        // 迭代查找出z的父结点，用y记录
        y = x
        if z.key < x.key
            x = x.left
        else
            x = x.right
    z.p = y                 // z的父结点为y
    if y == T.nil
        T.root = z          // y为空(NIL)，则z为根结点
    else if z.key < y.key
        y.left = z          // z小于y，则z为y的左孩子
    else
        y.right = z         // z大于y，则z为y的右孩子
    z.left = T.nil          // 设置边界，让z的左右孩子为T.nil
    z.right = T.nil
    z.color = RED           // 设置颜色红色
    RB-INSERT-FIXUP(T, z)   // 修复红黑性质

  可以看出红黑树插入操作与二叉查找树相似，区别在于：（1）TREE-INSERT内的所有NIL都被T.nil代替。（2）RB-INSERT的第17~18行置z的左右孩子为T.nil，以保持合理的树结构。（3）在第19行将z着为红色。（4）因为将z着为红色可能违反其中的一条红黑性质，在第20行中调用RB-INSERT-FIXUP来修复红黑性质。

  现在我们分析一下插入了一个红色结点后，有哪些红黑性质会被破坏？ 显然性质1（结点非红即黑）和性质3（叶结点T.nil为黑色）继续成立，性质5（任一结点到叶结点的所有简单路径上黑结点个数相同）因为并没有给哪条路径增加黑结点，所以也成立。那么可能被破坏的就是性质2（根结点为黑色）和性质4（不能有连续两个红结点）。接下来看RB-INSERT-FIXUP是如何修复红黑性质的。

红黑树插入修复伪代码（参考自《算法导论》）：

RB-INSERT-FIXUP(T, z)
    while z.p.color == RED                 // 当z的父结点为红色，循环继续
        if z.p == z.p.p.left               // 父结点是祖父结点的左孩子的情况
            y = z.p.p.right                // y指向祖父结点的右孩子，即叔结点
            if y.color == RED              // 如果叔结点为红色
                z.p.color = BLACK          // case 1  父结点置为黑色
                y.color = BLACK            // case 1  叔结点置为黑色
                z.p.p.color = RED          // case 1  祖父结点置为红色
                z = z.p.p                  // case 1  将z指向其祖父结点
            else                           // 否则，叔结点为黑色
                if z == z.p.right          // 如果z为父结点的右孩子
                    z = z.p                // case 2  z指向其父结点
                    LEFT-ROTATE(T, z)      // case 2  对z左旋
                                           // 到这里表明z为父结点的左孩子
                z.p.color = BLACK          // case 3  父结点置为黑色
                z.p.p.color = RED          // case 3  祖父结点置为红色
                RIGHT-ROTATE(T, z.p.p)     // case 3  对祖父结点右旋
        else(same as then clause with "right" and "left" exchanged)
            // 父结点是祖父结点的右孩子的情况，对应第3行的判断。这里将上面4~17行代码中right和left调换一下就行
    T.root.color = BLACK        // 根节点置为黑色

现在我们分析插入一个红色结点z后可能出现的情况：

（1）z为根结点。 破坏了性质2，直接将根结点置为黑色就好。

（2）z的父结点为黑色。 无任何红黑性质被破坏，不做处理。

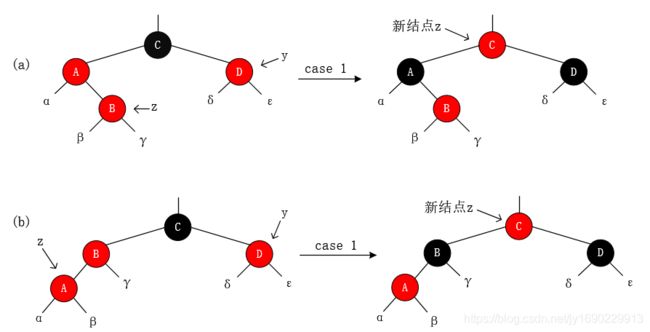
（3）z的父结点为红色。 破坏了性质4，这种情况对照RB-INSERT-FIXUP中的while循环，分两种情况处理：z的父结点是祖父结点的左孩子、z的父结点是祖父结点的右孩子。这两种情况处理方法类似（见代码第18行），我们就前一种进行分析，那么这种情况又分为3种情况：

  情况 1：z的叔结点是红色的。

​  情况 2：z的叔结点是黑色的，且z是一个右孩子。

​  情况 3：z的叔结点是黑色的，且z是一个左孩子。

下面我们将上述3个情况单独拿出来分析：

情况 1：z的叔结点y是红色的

处理步骤：（1）将z的父结点和叔结点都置为黑色

     （2）将z的叔结点都置为黑色

     （3）将z的祖父结点置为红色

​     （4）将z指向其祖父结点

说明：这样做不会造成性质2、4以外的红黑性质被破坏。

目的：修复z位置处的红黑性质，将破坏红黑性质的“结点”上移。若新结点z为根，而根的父结点指向T.nil，while循环终止，将根着为黑色，红黑性质修复；若新结点z（非根）的父结点为黑色，while循环终止，红黑性质修复；若新结点z（非根）的父结点为红色，while循环继续。

图例：

注：α、β、γ、δ、ε表示任意子树，下同。

情况 2：z的叔结点y是黑色的，且z是一个右孩子。

处理步骤：（1）先将z指向父结点

     （2）对z进行左旋

目的：将情况2转化为情况3。

图例见下图。

情况3：z的叔结点y是黑色的，且z是一个左孩子。**

处理步骤：（1）将z的父结点置为黑色

     （2）将z的祖父结点置为红色

     （3）对z的祖父结点进行右旋

目的：性质4得到修复，并且没有引起新的性质被破坏，红黑性质修复完成。

图例见下图。

注意：情况2和情况3中叔结点y可能为T.nil结点。 解释：若z为插入结点，则y为T.nil，因为插入前树必须符合红黑性质；若y为普通黑结点（非T.nil），则z为迭代变换中对z重新赋值产生的新结点z。

下面来看一个完整的插入修复案例：

四、删除

相比插入，红黑树的删除就要复杂很多。先看两个在删除要用到的操作：RB-TRANSPLANT(T,u,v)，表示用子树v去取代子树u；TREE-MINIMUM(x)，查找出以x为根的子树的最小结点。

它们的伪代码如下（参考自《算法导论》）：

RB-TRANSPLANT(T, u, v)
    if u.p == T.nil          // u的父结点为T.nil，说明u为根结点
        T.root = v           // v成为新的根结点
    else if u == u.p.left    // 若u是他爹的左孩子
        u.p.left = v         // u的爹重新认v为左孩子
    else                     // 若u是他爹的右孩子
        u.p.right = v        // u的爹重新认v为右孩子
    v.p = u.p                // v认u的爹为爹

TREE-MINIMUM(x)
    while x.left != T.nil
        x = x.left
    return x

红黑树删除过程：先将红黑树当作二叉查找树，将结点删除，然后通过一系列的重新着色和旋转操作，使树恢复红黑性质。

红黑树的删除与二叉查找树的删除原理是一致的，只不过删除之后要考虑修复红黑性质。结合下图分析从一个红黑树T中删除结点z可能出现的4种情况：

• z没有左孩子（即左孩子为T.nil）（图(a)），则用其右孩子来替换z，这个右孩子可以是T.nil，也可以不是，所以这种情况包含了两种情形：z没有孩子、z只有一个右孩子。

• z有左孩子，没有右孩子（图(b)），则用其左孩子来替换z。

• z既有左孩子又有右孩子。我们找z的右子树的最小结点y来替换z，因为这样能继续保证左孩子<父结点<右孩子。这种情况下y可以分为两种情况处理：

  • y是z的右孩子（图(c)），则直接用y替换z。
  • y不是z的右孩子（图(d)），则先用y的右孩子替换y，然后再用y替换z。

  这两种情况用y替换z后，y的颜色要变为z的颜色。
  
  
  

注：虚线表示省略任意多的结点及其子孙结点。

红黑树删除伪代码（参考自《算法导论》）：

RB-DELETE(T, z)
    y = z                                  // y指向z
    y-original-color = y.color             // 记录y的颜色
    if z.left == T.nil                     // 如果z的左孩子是T.nil
        x = z.right                        // x指向z的右孩子
        RB-TRANSPLANT(T, z, z.right)       // 用z的右孩子替换z
    else if z.right == T.nil               // 如果z有左孩子并且z的右孩子是T.nil
        x = z.left                         // x指向z的左孩子
        RB-TRANSPLANT(T, z, z.left)        // 用z的左孩子替换z
    else                                   // 如果z既有左孩子又有右孩子
        y = TREE-MINIMUM(z.right)          // y指向z的右子树的最小结点
        y-orighinal-color == y.color       // 记录y的颜色
        x = y.right                        // x指向y的右孩子
        if y.p == z                        // 如果y的父结点是z
            x.p = y                        // 因为x可能为T.nil结点，所以需要指明x的父结点
        else                               // 如果y的父结点不是z
            RB-TRANSPLANT(T, y, y.right)   // 用y的右孩子替换y
            y.right = z.right              // y认z的右孩子为自己的右孩子
            y.right.p = y                  // y的右孩子认y为父
        RB-TRANSPLANT(T, z, y)             // y替换z
        y.left = z.left                    // y认z的左孩子为自己的左孩子
        y.left.p = y                       // y的左孩子认y为父
        y.color = z.color                  // y的颜色变为z的颜色
    if y-original-color == BLACK           // y的初始颜色为黑色
        RB-DELETE-FIXUP(T, x)              // 修复红黑性质

结合上图分析上述代码：

• y始终为被删除的结点或被移动的结点。当z的子结点少于两个时，y指被删除的结点z；当z有两个子结点时，y指被移动的结点，也就是z的右子树的最小结点。当y为被移动的结点时，y替换z，y的颜色会变为z的颜色，这样y的颜色被删除，相当于y被“删除”。所以y始终可以看成是被“删除”的结点。

• 由于y被”删除“，可能引起红黑性质被破坏，所以用变量y-original-color来记录y的初始颜色。

• x作为y的子结点，将移至y的原始位置，又由于y被“删除”，这样就相当于x取代了y，那么结点x就是可能会造成红黑性质被破坏的地方，所以从结点x处开始修复红黑性质（见代码第25行）。

最后，由于是y被“删除”，如果y的颜色是黑色，必然会引起一个或多个红黑性质被破坏，所以在第25行调用RB-DELETE-FIXUP来恢复红黑性质。如果y的颜色为红色，红黑性质仍然保持，因为结点z的位置到叶结点的简单路径上的黑结点数目并没有改变。

那么，如果y是黑色的，可能造成哪些红黑性质被破坏呢？

1. 如果y是原来的根结点，而y的一个红色的孩子x成为新的根结点，这就违反了性质2。
2. 如果x和x.p是红色的，则违法了性质4。
3. 由于y被“删除”，导致先前包含y的任何简单路径上黑结点个数减1。因此，y的任何祖先都不满足性质5。

为了改正这些问题，我们先假设x还附带一个黑色，这样性质5成立，但x有两个颜色，即“红黑”或“黑黑”，这样破坏了性质1，所以现在的问题变为修正性质1、性质2和性质4。下面我们来看RB-DELETE-FIXUP是如何修复这些红黑性质的。

红黑树删除修复伪代码（参考自《算法导论》）：

RB-DELETE-FIXUP(T, x)
    while x != T.root && x.color == BLACK     // 当x不为根且x是黑色的，循环继续
        if x == x.p.left                      // 如果x是一个左孩子
            w = x.p.right                     // 将w指向兄弟结点
            if w.color == RED                 // 如果w是红色的
                w.color = BLACK               // case 1  w的颜色置为黑色
                x.p.color = RED               // case 1  x的父结点置为红色
                LEFT-ROTATE(T, x.p)           // case 1  对x的父结点进行左旋
                w = x.p.right                 // case 1  将w指向x的新的兄弟结点
            if w.left.color == BLACK && w.right.color == BLACK
                                              // 如果w的左右孩子均为黑色的
                w.color = RED                 // case 2  w的颜色置为红色
                x = x.p                       // case 2  将x指向x的父结点
            else                              // 如果w有至少一个子结点是红色的
                if w.right.color == BLACK     // 如果w的右孩子是黑色的
                    w.left.color = BLACK      // case 3  w的左孩子置为黑色
                    w.color = RED             // case 3  w的颜色置为红色
                    RIGHT-ROTATE(T, w)        // case 3  对w进行右旋
                    w = x.p.right             // case 3  将w指向x的新的兄弟结点
                w.color = x.p.color           // case 4  将w的颜色置为与x的父结点同色
                x.p.color = BLACK             // case 4  x的父结点置为黑色
                w.right.color = BLACK         // case 4  w的右孩子置为黑色
                LEFT-ROTATE(T, x.p)           // case 4  对x的父结点进行左旋
                x = T.root                    // case 4  将x指向根结点
        else (same as then clause with "right" and "left" exchanged)
            // 如果x是一个右孩子，与x是一个左孩子的情况一样，不过要将right和left互换
    x.color = BLACK                           // 根结点置为黑色

分析RB-DELETE-FIXUP的修复过程，其中while循环的目标是将x所附带的黑色沿树上移，直到出现下面的情况：

（1）x指向“红黑”结点，此时在第27行中，将x置为（单个）黑色。

（2）x指向根结点，此时可以简单地”移除“这个附带的黑色。

（3）执行适当的旋转和重新着色，退出循环。

上述情况可以归纳为以下3种情况：

1. x指向”红黑“结点。

   解决方法：将x置为（单个）黑色。到此红黑性质全部修复。

2. x指向”黑黑“结点，且x为根结点。

   解决方法：”移除“这个附带的黑色，即不做任何处理，直接结束。到此红黑树性质全部修复。

3. x指向”黑黑“结点，且x不为根结点。解决方法：这里分为4种情况处理：

   情况1：x的兄弟结点w是红色的。

   情况2：x的兄弟结点w是黑色的，且w的两个子结点都是黑色的。

   情况3：x的兄弟结点w是黑色的，w的左孩子是红色的，w的右孩子是黑色的。

   情况4：x的兄弟结点w是黑色的，且w的右孩子是红色的。

下面将上述4种情况单独拿出来分析：

情况1：x的兄弟结点w是红色的。

注：α、β、γ、δ、ε、ζ表示任意子树，下同。

处理步骤：（1）w的颜色置为黑色

     （2）x的父结点置为红色

     （3）对x父结点进行左旋

     （4）将w指向x的新的兄弟结点

说明：这样做不违反红黑性质。

目的：x的新的兄弟结点是旋转之前w的某个黑色子结点，这样，就将情况1转化成情况2、3或4来处理。

情况2：x的兄弟结点w是黑色的，且w的两个子结点都是黑色的。

注：白色结点表示该结点可能是黑色，也可能是红色，下同。

处理步骤：（1）w的颜色置为红色

     （2）将x指向x的父结点

说明：由于新的x结点附带一个黑色，弥补了因w置为红色而损失的黑色，所以这样做不违反红黑性质。

目的：将x所附带的黑色上移，若新的x结点是“红黑”结点或根结点，则while循环终止，否则循环继续。

情况3：x的兄弟结点w是黑色的，w的左孩子是红色的，w的右孩子是黑色的。

处理步骤：（1）w的左孩子置为黑色

     （2）w的颜色置为红色

     （3）对w进行右旋

     （4）将w指向x的新的兄弟

说明：这样做不违反红黑性质。

目的：新的w结点的右孩子变为红色，这样就将情况3转化成情况4。

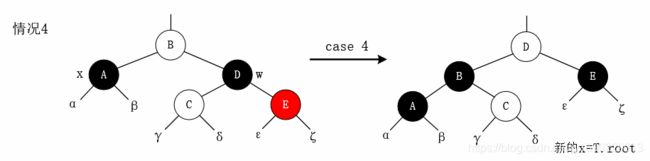
情况4：x的兄弟结点w是黑色的，且w的右孩子是红色的。

处理步骤：（1）将w的颜色置为与x的父结点同色

​     （2）x的父结点置为黑色

​     （3）w的右孩子置为黑色

     （4）对x的父结点进行左旋

     （5）将x指向根结点

说明：这样做不违反红黑性质。

目的：从根结点，经过x，到叶子结点的所以简单路径上，黑色结点个数增加1，相当于将x所附带的黑色，转移给了一个未着色的结点，这样红黑性质得到修复。x指向了根结点，终止while循环。

下一篇：《算法导论》红黑树详解（二）：Java实现Demo

参考书籍：《算法导论》第3版