剑指offer刷题详细分析:part5:21题——25题
-
剑指offer所有题目详解,可访问我的github项目:KongJetLin-offer
-
目录
- Number21:栈的压入、弹出序列
- Number22:从上往下打印二叉树
- Number23:二叉搜索树的后序遍历序列
- Number24:二叉树中和为某一值的路径
- Number25:复杂链表的复制
题目22 栈的压入、弹出序列
题目描述:输入两个整数序列,第一个序列表示栈的压入顺序,请判断第二个序列是否可能为该栈的弹出顺序。假设压入栈的所有数字均不相等。例如序列1,2,3,4,5是某栈的压入顺序,序列4,5,3,2,1是该压栈序列对应的一个弹出序列,但4,3,5,1,2就不可能是该压栈序列的弹出序列。(注意:这两个序列的长度是相等的)
我们建立一个辅助栈,根据给出的出栈序列,我们对入栈序列进行出栈入栈的动作,进而判断该序列是否可能正确。
根据弹出序列,我们依次进行判断。我们新建一个新栈,将压栈序列的数字压入新栈中,如果弹出序列下一个要弹出的数字刚好是新栈栈顶数字,那么直接弹出;如果弹出序列下一个要弹出的数字不在新栈栈顶,则把压栈序列中还没有入栈的数字压入栈中,直到将下一个要弹出的数字压入新栈栈顶为止,如果所有的压栈序列的数字都压入新栈中后,仍然没有找到下一个要弹出的数字,说明此时要弹出的数字已经从压栈序列取出,放入在新栈中,那么该弹出序列就不可能是一个当前压栈序列的弹出序列。
给出两个例子如下:

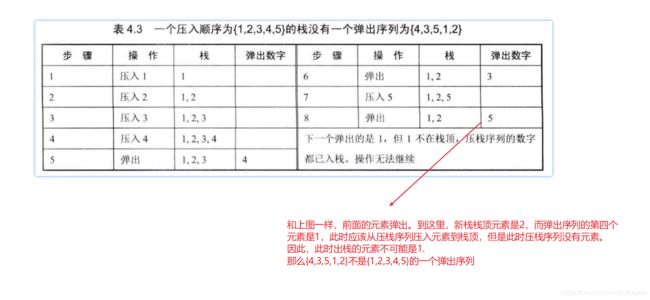
代码如下:
public static boolean IsPopOrder(int [] pushA,int [] popA)
{
//当2个序列数组有一个位null,或者2个序列数组的长度不一致,不满足,直接返回false
if(pushA == null || popA == null || pushA.length!=popA.length)
return false;
//对于栈,java推荐性能更好的ArrayDeque,而不是Stack
ArrayDeque<Integer> stack = new ArrayDeque<>();
int pushIndex = 0;//压栈序列的下标
//堆出栈序列 popA进行遍历
for (int i = 0; i < popA.length ; i++)
{
//如果新栈 stack不为null,且栈顶元素是目前出栈序列要出栈的元素,直接出栈
if(!stack.isEmpty() && popA[i] == stack.peek())//注意,先判断stack是否为null,否则stack.peek()=null.peek(),出现空指针异常
{
stack.pop();//出栈栈顶元素
}
else
{
/**
如果栈顶元素不是当前出栈序列要出栈的元素,则当 pushIndex
while(pushIndex < pushA.length)
{
stack.push(pushA[pushIndex]);//将压栈序列的元素压入stack
//只要压栈序列有一个元素压入stack,不管stack栈顶元素能不能满足pop[i],pushA下标必须加1,因此需要在break之前加1
pushIndex++;
if(stack.peek() == popA[i])
{//当stack栈顶元素是pop[i],将栈顶元素出栈,并且跳出while循环,判断下一个pop[i]
stack.pop();
break;
}
}
/**
结束while循环有2种情况:
1)stack.peek() == popA[i],break结束
2)pushA元素入栈stack完毕,此时 stack.peek() != popA[i],pushIndex = pushA.length,角标越界,结束循环
*/
}
}
/**
说明:
1)在while循环中,如果pushA元素入栈stack完毕,此时 stack.peek() != popA[i],while循环结束,此处说明 popA不是pushA的弹出序列。
此时for循环就会跳过这一层 pop[i]的判断,判断下一个元素 pop[i+1]是不是stack栈顶元素。
那么不管怎么样,总体上 stack最后最少少出栈一个元素,假设 pushA与popA的大小都是n,stack里面所有经过的元素数目=PushA元素数目=n,
这里stack少出栈一个popA[i],那么stack最后肯定不为empty;
2)如果popA是pushA的弹出序列,由于 pushA.length=popA.length=stack的所有经过元素数目,stack最后一定为null!
返回时,stack=empty,返回true,否则返回false
*/
return stack.isEmpty();
}
- 注:这里参考文章:添加链接描述
题目22 从上往下打印二叉树
题目描述:从上往下打印出二叉树的每个节点,同层节点从左至右打印。
分析:这是二叉树的层序遍历(广度优先遍历),我们使用一个队列来辅助。
public ArrayList<Integer> PrintFromTopToBottom(TreeNode root)
{
ArrayList<Integer> arrayList = new ArrayList<>();
//注意,这一题如果root为null的时候,我们直接返回arrayList即可
//否则因为根结点为空,queue.add(root) 的时候回出现空指针异常
if(root == null)
return arrayList;
Queue<TreeNode> queue = new LinkedList<>();//创建一个队列,注意,LinkedList实现了Queue接口,它也可以算作队列
queue.add(root);//先将二叉树根结点添加进来
while (!queue.isEmpty())
{
TreeNode cur = queue.remove();
arrayList.add(cur.val);//将队首结点出队,并将该结点的值添加到ArrayList
if(cur.left != null)
queue.add(cur.left);
if(cur.right != null)
queue.add(cur.right);
}
return arrayList;
//运行时间:14ms,占用内存:9420k
}
题目23 二叉搜索树的后序遍历序列
题目描述:输入一个非空整数数组,判断该数组是不是某二叉搜索树的后序遍历的结果。如果是则输出Yes,否则输出No。假设输入的数组的任意两个数字都互不相同。
分析:如果这个数组的元素是二叉搜索树的后序遍历序列,这个数组的元素应该是这样组成的: [ 小数序列 大数序列 中间的数(唯一)],其中这个中间数就是当前树的根结点,对于每一个左右子树,也应该满足这个序列。且小数序列就是当前根结点的左子树的结点,大数序列就是当前根结点右子树的结点。
那么我们从头开始遍历,当数小于 中间根结点的数的时候,持续遍历,直到找到一个下标为 cutIndex 数大于中间的数,从 cutIndex 开始,判断下面的数是否全部大于中间的数。如果遍历完全部大于,开始遍历 小数序列组成的左子树 以及 大数序列组成的右子树,同样分成 [ 小数序列 大数序列 中间的数(唯一)],最后一个数是子树根结点的数,也是中间的数。如果不满足,则返回false,即不是二叉搜索树的后序遍历序列。
具体分析如下代码:
public boolean VerifySquenceOfBST(int [] sequence)
{
//先判断数组是否合法
if(sequence == null || sequence.length == 0)
return false;
//验证以 数组中下标为 0 到 sequence.length-1的数 是否二分搜索树的后序遍历序列
//其中,sequence.length-1 为最大的二分搜索树的根
return verify(sequence , 0 , sequence.length-1);
}
//验证以 数组中下标为 start 到 end 的数 是否二分搜索树的后序遍历序列
private boolean verify(int[] sequence , int start , int end)
{
/*
最后的情况:
当遍历到的数组有3个数,即 end - start = 2,此时二叉树可能是:
(1) (2) (3) (4)
n1 n1 n1 n1 n1
/ \ 或者 / 或者 \ 或者 / 或者 \
n2 n3 n2 n2 n2 n2
/ \ \ /
n3 n3 n3 n3
此时二叉搜索树还有可能不是后序遍历排列,我们还需将序列继续判断拆分;
拆分后如果是第一种,对于左右子树都是 end - start=0,只有最后一个叶子结点,此时必然是后序遍历;
如果是第二种,左子树或者右子树 end-start=1,结构如下:
n2 n2
/ 或者 \
n3 n3
此时,注意到数组的每个数都不一样,那么n2!=n3,此时不管 n2>n3 或者 n3>n2 ,都可能对应某一个结构的后序遍历数列,
n2>n3 对应上面(1)(4), n3>n2 对应上面(2)、(3)。
即当数组中只有2个数的时候,他们组成的二叉树必然满足某一结构二叉树的后序遍历序列,不需要继续拆分。
当然,还有可能出现下面 while中 cutIndex=end的情况,即没有右子树,此时右子树的判断中:end-start<0
那么,我们判断的时候判断 end-start<=1即可,即end-start可能为0或者1或者-1<0!
当然,对于这里2个数的二叉树结构,也可以继续拆分,可能出现 end-start<=0的情况,下面判断 end-start<=0即可!!
这里去除1的含义是将2个数的二叉树结构继续拆分。
总结:当 end-start <=1 的时候,整个树满足二叉搜索树的后序遍历序列,返回true
*/
if(end - start <=1)
return true;
//找到当前二分搜索树的根结点的值(中间值)
int midValue = sequence[end];
//定义一个指针,来将 [ 小数序列 大数序列 中间的数(唯一)] 小数序列与大数序列分开,这个值从start开始寻找
int cutIndex = start;
//当指针没有指向数组最后一个值:二分搜索树的根结点,且指针指向的数组的数小于根结点的值得时候,持续向下遍历
while(cutIndex < end && sequence[cutIndex] < midValue)
cutIndex++;
//当跳出循环,要么cutIndex=end,此时说明没有大数序列,但是还需向下判断,此时大数序列 end(end-1)-start(cutIndex=end)=-1<0,返回true。而小数序列需要继续判断;
// 要么 sequence[cutIndex] > midValue ,遍历完小数序列
//cutIndex位置为大数序列的第一个数,当cutIndex
//如果全部大于,说明大数序列存在,继续判断子树;
// 如果找到一个不大于,那么说明大数序列不存在,数组是 “小数 大数 小数 大数...”循环的模式,不是后序遍历序列,返回false
for (int i = cutIndex; i < end ; i++)
{
if(sequence[i] < midValue)//注意这里是 sequence[i] ,不是sequence[cutIndex]
return false;
}
//如果当前的序列满足,那么继续判断大数序列和小数序列(即当前根结点的左右子树)是否满足后序遍历,一次递归只能判断一层
// 大数序列(右子树)的数组字段是:cutIndex —— end-1;小数序列(左子树)的数组字段是:0 —— cutIndex-1
return verify(sequence , 0 , cutIndex-1) && verify(sequence , cutIndex , end-1);
}
题目24 二叉树中和为某一值的路径
题目描述:输入一颗二叉树的根节点和一个整数,打印出二叉树中结点值的和为输入整数的所有路径。路径定义为从树的根结点开始往下一直到叶结点所经过的结点形成一条路径。
/**
* 这一题需要注意:打印出二叉树中结点值的和为输入整数的所有路径
* 是要找到所有的路径,不是单单找到某一个满足的路径
*/
//首先,我们创建一个成员的ArrayList:ret,ret用于存储 保存了各个路径结点的ArrayList:temp
private ArrayList<ArrayList<Integer>> ret = new ArrayList<>();
//这个方法用于 找到所有满足的路径
public ArrayList<ArrayList<Integer>> FindPath(TreeNode root, int target)
{
ArrayList<Integer> temp = new ArrayList<>();//用于保存路径结点的ArrayList
//回溯/折回 保存结点的方法:这个方法用于找出以 root 为结点的满足条件的路径,并将路径保存到temp,再将 temp 保存到ret
backtracking(root , target , temp);
//将添加了结点的ret返回
return ret;
}
private void backtracking(TreeNode node, int target , ArrayList<Integer> temp)
{
//首先,如果递归到叶子结点后面,已经没有其他结点了,我们不需要再添加结点到 temp,直接结束函数,结束添加
if(node == null)
return;
int val = node.val;
temp.add(val);//将结点的值添加到temp中
target -= val;//target减去node结点的值
/**
* 1)当递归到叶子结点,且target=0,此时这一路径 temp 满足条件,将其添加到ret
* 2)如果 target=0,但是没有递归到叶子结点,会继续往 node 的左右子树递归,直到递归到node=null结束递归,此时target<0,下面的路径都不会添加到ret;
* 如果target!=0,递归到叶子结点,不会讲temp添加到ret,再次进入node的左右结点(都为null),直接结束递归;
* 如果 target!=0且没有递归到叶子结点,持续向左右子树进行结点的添加;
*
* 另外,不管是添加此路径到ret,还是向左右子结点递归,我们都要在temp中删除当前结点,前面已经将包含当前结点的路径添加到ret(满足的话,不满足也遍历过包含当前结点的路径)
* 我们将当前结点从temp中剔除,返回上一级递归,上一级递归就可以添加上一级node的右孩子结点,形成新的路径;或者上一级node的右子树也遍历完毕,
* 就会删除上一级的node,继续向上回递归。
* 这样,我们就可以通过一个temp,就将以root为根的所有路径都遍历一遍,并将满足的路径添加到ret(画个图就明白,重要的是最后一步,删除temp中的当前结点)
*/
if(target == 0 && node.left == null && node.right == null)
{
/*
注意!!,这里我们不能直接将temp放入ret中,因为最后可能有多条路径,如果直接将temp放入ret中,
那么下一次我们再次找到新的路径,将temp放入ret中,由于是同一个temp引用,后面的路径就会覆盖前面的路径,
因此我们需要使用 ArrayList(Collection c) 这个构造方法,将temp内部的元素new成为一个新的ArrayList,再添加到ret
*/
ret.add(new ArrayList(temp));
}
else
{
backtracking(node.left , target , temp);
backtracking(node.right , target , temp);
}
//当回递归到这里,node结点的值就保存在temp的尾部(因为后面的node也删除了),那么删除temp的最后一个元素即可
temp.remove(temp.size()-1);
}
题目25 复杂链表的复制
题目描述:输入一个复杂链表(每个节点中有节点值,以及两个指针,一个指向下一个节点,另一个特殊指针random指向一个随机节点),请对此链表进行深拷贝,并返回拷贝后的头结点。(注意,输出结果中请不要返回参数中的节点引用,否则判题程序会直接返回空)。
分析:首先,我们不能像普通单链表复制一样操作,因为普通单链表的结点只有一个指针指向next,而复杂链表的结点有一个随机指针,如果我们从头到尾一个一个复制,random指针可能找不到指向。具体操作如下:
解题方法:
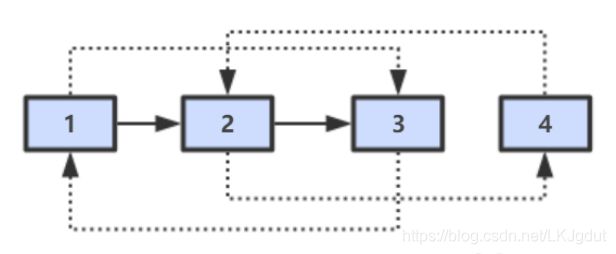
1)第一步,在每个节点的后面插入复制的节点。

2)第二步,对复制节点的 random 链接进行赋值。
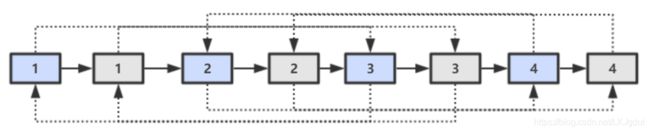
3)第三步,拆分。

代码如下:
public RandomListNode Clone(RandomListNode pHead)
{
//注意必须要判断pHead是否为null
if(pHead == null)
return null;
//1、在每个节点的后面插入复制的节点
RandomListNode cur = pHead;
while(cur != null)
{
RandomListNode clone = new RandomListNode(cur.label);
//将复制的结点连接到链表上
clone.next = cur.next;
cur.next = clone;
//将cur后移2位
cur = clone.next;
}
//2、对复制节点的 random 链接进行赋值
cur = pHead;
while (cur != null)
{
RandomListNode clone = cur.next;
//当cur的随机指针不指向null的时候,将cur复制结点的指针指向相应位置
if(cur.random != null)
{
clone.random = cur.random.next;//复制结点的random指向原来cur结点random指向结点的下一个结点
}
cur = clone.next;//将cur后移2位
}
//3、拆分
cur = pHead;
RandomListNode pHeadClone = pHead.next;//首先定义一个指针指向复制链表的头结点,用于返回
/**
这里的功能是将当前结点cur的指针指向下一个结点的下一个结点。
画图可知,当cur.next(当前结点的下一个结点)存在的时候,才有必要将当前结点的next指针指向下下个结点(不管下下个结点是否为null),
如果cur.next=null,说明以及到达链表结尾,不需要继续指向。(只有cur.next存在的时候,才有下下个结点!)
如果不判断 cur.next 存在,那么nextNode.next会出现空指针异常(nodeNode.next = null.null)
*/
while(cur.next != null)
{
RandomListNode nextNode = cur.next;
cur.next = nextNode.next;//使得当前结点的next指针指向下下个结点
cur = nextNode;//将当前指针只后移一位,因为链表中每一个结点的指针都需要指向下下个结点(当cur.next=null的时候不需要)
}
return pHeadClone;
}
注:此处参考大佬CYC2018的题解