迪杰斯特拉（Dijkstra）算法（D算法）：最短寻径问题

1，应用场景—最短寻径问题

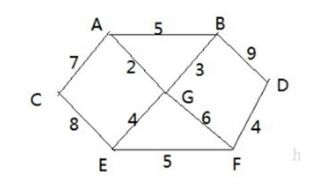
• 如图，存在7个村庄['A', 'B', C', 'D', 'E', 'F', 'G']，现在有6个邮差，从G点出发，需要分别赶往['A', 'B', C', 'D', 'E', 'F']六个村庄
• 各个村庄的距离通过边的权值表示，如A <-> B = 5
• 问：如何计算G村庄到其他村庄的最短距离
• 注意：之前两篇说的普里姆算法和克鲁斯卡尔算法，都是求图内连接各个节点的最短路径；该问题是从一点出发，到各个顶点的最短路径。注意，此处是到各个顶点，不是总和的最短路径

2，迪杰斯塔拉算法介绍

• 首先构建出图的顶点集合和邻接图表，并确定出发顶点
• 然后根据图表信息和出发顶点信息构建顶点访问情况对象，其中包括三个数组属性：
  • 顶点访问情况数组：0表示未访问， 1表示已访问
  • 顶点距离数组：各个顶点到出发顶点的最短距离汇总，也是最终的结果；出发顶点到出发顶点的距离为0，其他顶点到出发顶点的距离初始化为极值
  • 前驱顶点数组：即访问当前顶点的上一个顶点，经过几次前继查找，必定会查找到出发顶点，该数组可能计算完成后，用户复原路线图

• 构建完成后，开始进行计算
  1. 先处理出发顶点，处理之前，先标记当前顶点为已访问，然后从邻接图标中获取该顶点的连接数组，用户顶点距离数组填充，已连接的填充真实距离，未连接的填充为极值（此处注意，出发节点与部分节点未连通，后续处理中会广度遍历其他节点，判断连通）；之后将所有连接节点的前驱节点修改为出发节点
  2. 出发顶点处理完成后，对所有与出发顶点关联的节点已经初步统计完成；但是，此处还存在间接关联的节点没有统计；另外，直接连接的距离不一定比间接连接的距离近，比如A-B=5，B-C=10，A-C=20，这样从A-B-C=15，间接距离是小于直接距离的（此处可不用考虑合理性，只做场景分析，不排除翻山越岭）
  3. 出发顶点处理完成后，按照图广度遍历优先的原则，从距离数组中，依次取出距出发顶点距离最小的未访问顶点，进行访问顶点处理
  4. 访问顶点在遍历顶点集合判断距离时，用访问顶点到出发顶点的距离与访问顶点到当前遍历顶点的距离之和（出发顶点通过间接方式到当前遍历顶点的距离），与当前遍历顶点到出发顶点的距离（直接方式到当前遍历顶点的距离，不存在直接方式则为极值）取最小值，进行顶点距离和顶点前驱节点的覆盖
  5. 循环第3，第4步，直到所有顶点全部为已访问，则计算完成
• 计算全部完成后，顶点访问情况对象里面的顶点距离数组，即为最终的结果呈现！

3，代码实现

package com.self.datastructure.algorithm.dijkstra;

import lombok.Getter;

import java.util.Arrays;

/**
 * 迪杰斯特拉算法_D算法
 * * 先通过连通图和出发顶点构建一个访问过的顶点对象
 * * 该对象中包括: 标记顶点访问情况的数组, 顶点到出发顶点的距离数组, 顶点的前驱顶点数组
 * * 从出发顶点开始, 标记该顶点已经访问, 并计算各个顶点到该顶点的距离, 其中不连通的用一个极值表示
 * * 之后继续依照广度搜索优先的算法原则, 依次向外扩展
 * * 从与出发顶点连接的顶点的中, 依次找到距离最小的未访问顶点进行访问并刷新访问状态, 距离和前驱节点
 * * 直至所有顶点遍历完成后, 距离数组中的数据即为最短距离数据
 * @author pj_zhang
 * @create 2020-07-12 12:40
 **/
public class Dijkstra {

    private static final int NON = Integer.MAX_VALUE;

    public static void main(String[] args) {
        // 顶点列表
        char[] lstVertex = {'A', 'B', 'C', 'D', 'E', 'F', 'G'};
        // 顶点图
        int[][] vertexMap = {
                {NON, 5, 7, NON, NON, NON, 2},
                {5, NON, NON, 9, NON, NON, 3},
                {7, NON, NON, NON, 8, NON, NON},
                {NON, 9, NON, NON, NON, 4, NON},
                {NON, NON, 8, NON, NON, 5, 4},
                {NON, NON, NON, 4, 5, NON, 6},
                {2, 3, NON, NON, 4, 6, NON}
        };
        MyGraph myGraph = new MyGraph(lstVertex, vertexMap);
        dijkstra(myGraph);
    }

    /**
     * 开始迪杰斯塔拉算法
     * @param myGraph 连接图表
     */
    private static void dijkstra(MyGraph myGraph) {
        // index在此处作为出发顶点
        int index = myGraph.getVertexCount() - 1;
        // 初始化已经连接顶点类
        VisitedVertex visitedVertex = new VisitedVertex(myGraph.getVertexCount(), index);
        // 先从出发顶点, 修改连接顶点的距离和前置顶点
        updateVisitedVertex(visitedVertex, myGraph, index);
        // 出发顶点访问完成后, 还存在间接关联节点没有关联到
        // 同时直接关联顶点的距离不一定比间接关联的距离小
        // 所以此处参考图的广度遍历, 取还没有被访问过的距出发节点距离最小的顶点作为访问顶点继续处理
        // 因为已经访问了一个顶点, 所以此处少访问一个
        for (int i = 0; i < myGraph.getVertexCount() - 1; i++) {
            // index在此处重新赋值, 作为访问顶点
            index = getNextIndex(visitedVertex);
            // 从访问顶点继续修改顶点距离和前置顶点
            updateVisitedVertex(visitedVertex, myGraph, index);
        }
        System.out.println("最终结果: " + Arrays.toString(visitedVertex.getVertexDis()));
    }

    /**
     * 获取下一个未被访问的顶点
     * 注意此顶点一定要是距出发顶点距离最小的
     * @param visitedVertex
     * @return
     */
    private static int getNextIndex(VisitedVertex visitedVertex) {
        int[] visitedArr = visitedVertex.getVisitedArr();
        // 取最小距离为未连通状态下的最大距离
        int minDis = NON;
        int index = -1;
        for (int i = 0; i < visitedArr.length; i++) {
            if (visitedArr[i] == 0 && visitedVertex.getVertexDis()[i] < minDis) {
                index = i;
                minDis = visitedVertex.getVertexDis()[i];
            }
        }
        return index;
    }

    /**
     * 修改当前顶点下, 从出发顶点到各个顶点的距离
     * * 此处主要考虑存在顶点与出发顶点间接关联, 比如通过该顶点关联
     * * 则间接顶点到出发顶点的距离 = 当前顶点到出发顶点的距离 + 间接顶点到当前顶点的距离
     * @param visitedVertex 访问顶点记录对象
     * @param myGraph 顶点下标关联图
     * @param index 当前顶点下标
     */
    private static void updateVisitedVertex(VisitedVertex visitedVertex, MyGraph myGraph, int index) {
        // 标记当前访问顶点为已访问
        visitedVertex.getVisitedArr()[index] = 1;
        // 获取访问图
        int[][] vertexMap = myGraph.getVertexMap();
        // 当前顶点到各个顶点的距离图
        int[] distanceArr = vertexMap[index];
        for (int i = 0; i < distanceArr.length; i++) {
            // 遍历获取该顶点到每一个关联顶点的距离
            // 不为NON, 说明存在关联
            if (distanceArr[i] != NON) {
                // 如果当前顶点没有被访问
                // 并且当前顶点到访问顶点的距离 + 访问顶点到出发顶点的距离小于现有的当前顶点到访问的距离
                // 则进行替换, 并标记为前驱节点
                if (visitedVertex.getVisitedArr()[i] == 0
                        && (myGraph.getVertexMap()[index][i] + visitedVertex.getVertexDis()[index] < visitedVertex.getVertexDis()[i])) {
                    visitedVertex.getVertexDis()[i] = (myGraph.getVertexMap()[index][i] + visitedVertex.getVertexDis()[index]);
                    visitedVertex.getPreVertexArr()[i] = index;
                }
            }
        }
    }

    /**
     * 已访问顶点记录对象
     */
    @Getter
    static class VisitedVertex {

        /**
         * 已访问的顶点数组
         * 0表示未访问, 1表示已访问
         */
        private int[] visitedArr;

        /**
         * 顶点距离
         * 表示当前顶点到目标顶点的距离
         * 遍历过程中体现的是当前距离
         * 全部处理完成即最终结果
         */
        private int[] vertexDis;

        /**
         * 顶点的前驱顶点
         * 最后最后绘制连接图, 表示从出发顶点访问到当前顶点, 需要经过的路径
         */
        private int[] preVertexArr;

        /**
         * 初始化已连接顶点类
         * @param vertexCount 顶点数量
         * @param startIndex 出发顶点索引
         */
        public VisitedVertex(int vertexCount, int startIndex) {
            // 初始化已访问顶点数组
            this.visitedArr = new int[vertexCount];
            // 初始化距离数组
            this.vertexDis = new int[vertexCount];
            // 初始化距离为未连通距离
            Arrays.fill(vertexDis, NON);
            // 初始化出发节点距离为0
            this.vertexDis[startIndex] = 0;
            // 初始化前驱节点数组
            this.preVertexArr = new int[vertexCount];
        }

    }

    /**
     * 图表类
     */
    @Getter
    static class MyGraph {

        /**
         * 顶点数量
         */
        private int vertexCount;

        /**
         * 顶点列表
         */
        private char[] lstVertex;

        /**
         * 顶点连接图
         */
        private int[][] vertexMap;

        public MyGraph(char[] lstVertex, int[][] vertexMap) {
            this.vertexCount = lstVertex.length;
            this.lstVertex = lstVertex;
            this.vertexMap = vertexMap;
        }

    }

}