Python————动态规划

动态规划

一、动态规划

动态规划(dynamic programming)是运筹学的一个分支，是求解决策过程(decision process)最优化的数学方法。

• 科技公司面试必考算法

• 题目类型多， 没有固定的模板

• 难度属于中上

二、动态规划之Fib数列

问题描述

有个小孩上楼梯，共有N阶楼梯，小孩一次可以上1阶，2阶。走到N阶楼梯，一共有多少种走法？

思路分析

DP之自顶向下分析方式：
爬到第N阶楼梯，一共只有2种情况(全划分，加法原理)，从第N-1阶爬1阶到第N阶；从第N-2阶爬2阶到第N阶；
故：way(N)=way(N-1)+way(N-2)

代码实现

def fib(n):
	memo = [-1 for x in range(n+1)]
	memo[0] = 0
	memo[1] = 1
	memo[2] = 2
	for i in range(3,n+1):
		memo[i] = memo[i-1] + memo[i-2]
	return memo[n]
	

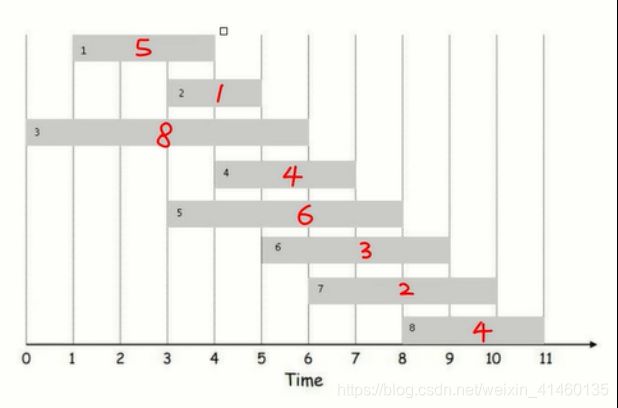
三、任务安排问题

代码实现

# 数组arr存储的是每个任务的收益；
arr = [0, 5, 1, 8, 4, 6, 3, 2, 4]
#数组prev存储的是指定任务之前可以执行的任务
prev = [0, 0, 0, 0, 1, 0, 2, 3, 5]

def dp_opt(arr):
    #计算任务的长度
    len_arr = len(arr)
    # 存储执行到每个任务可以获得的最优解;
    opt = [0 for i in range(len_arr)]
    opt[0] = 0
    opt[1] = arr[1]
    for i in range(2, len(arr)):
        # 不选择做这个任务的最优解；
        A = opt[i - 1]
        # 选择做这个任务的最优解；
        B = arr[i] + opt[prev[i]]
        opt[i] = max(A, B)
    return opt[-1]
print(dp_opt(arr))

四、不相邻树最大和

问题描述:

给定数组A=[1,2,4,1,7,8,3]，求出数组A中互不相邻的数的最大和。
例如：如果选择了8，则不能选择7和3，在本例中最大的和为1+4+7+3=15

代码实现：

arr = [1, 2, 4, 1, 7, 8, 3]


def dp_opt(arr):
    len_arr = len(arr)
    opt = [0 for i in range(len_arr)]
    opt[0] = arr[0]
    opt[1] = arr[1]
    for i in range(2, len_arr):
        A = opt[i - 1]
        B = arr[i] + opt[prev[i]]
        opt[i] = max(A, B)
    return opt