数据结构&算法-----(9)背包问题(dp&贪心)
数据结构&算法-----(9)背包问题
- 0-1 背包
- ① 求解背包所含物品的最大值
- ② 求出背包中装入物品的编号
- 二维dp代码实现
- 一维dp代码实现(滚动数组)
- 贪心算法,无法全局最优
- 多重背包
- 完全背包
- 二维dp代码实现
- 一维dp代码实现
- 便利蜂2020实习笔试第一题
- 贪心
- dp
去年夏天一直在便利蜂买椰奶喝,,做便利蜂的笔试题时,01背包问题死活只通过14%,这里再加深一下对背包问题的理解
笔试题代码已发在牛客网上:
便利蜂20200507笔试题(Java)
问题描述:
一个背包的总容量为V,现在有N类物品,第i类物品的重量为weight[i],价值为value[i]
那么往该背包里装东西,怎样装才能使得最终包内物品的总价值最大。
这里装物品主要由三种装法:
1、0-1背包:每类物品最多只能装一次
2、多重背包:每类物品都有个数限制,第i类物品最多可以装num[i]次
3、完全背包:每类物品可以无限次装进包内
0-1 背包
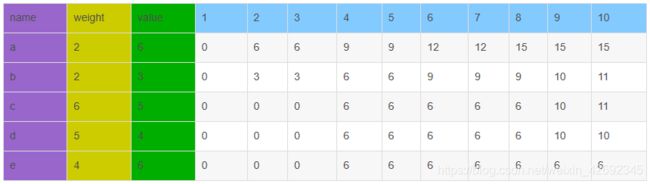
有编号分别为a,b,c,d,e的五件物品,它们的重量分别是2,2,6,5,4,它们的价值分别是6,3,5,4,6,现在给你个承重为10的背包,如何让背包里装入的物品具有最大的价值总和?
① 求解背包所含物品的最大值
利用动态规划求最优值的方法。假设用dp[N][V]来存储中间状态值,dp[i][j]表示前i件物品能装入容量为j的背包中的物品价值总和的最大值(注意是最大值),则我们最终只需求知dp[i=N][j=V]的值,即为题目所求。
假设我们已经求出前i-1件物品装入容量j的背包的价值总和最大值为dp[i-1][j],固定容量j的值不变,则对第i件物品的装法讨论如下:
1、首先第i件物品的重量weight[i]必须小于等于容量j才行,即
- 若
weight[i]>j,则第i件物品肯定不能装入容量为j的背包,
则有dp[i][j]=dp[i-1][j] - 若
weight[i]<=j,则首先明确的是这件物品是可以装入容量为j的背包的,那么如果我们将该物品装入,
则有dp[i][j]=dp[i-1][j-weight[i]]+value[i]
2、接下来要判断第i件物品装到容量为j的背包后,背包内的总价值是否是最大?
- 如果装了第
i件物品后的总价值dp[i-1][j-weight[i]]+value[i]>没装之前的总价值最大值dp[i-1][j],则肯是最大的; - 反之则说明第
i件物品不必装入容量为j的背包(装了之后总价值反而变小,那么肯定就不需要装嘛)
故,状态转移方程为:dp[i][j] = Max { dp[i-1][j] , dp[i-1][j-weight[i]] + value[i] }
注意:这里的前i件物品是给定次序的
这张表是至底向上,从左到右生成的
注意dp遍历的方向
用e2单元格表示e行2列的单元格:表示只有物品e时,有个承重为2的背包,那么这个背包的最大价值是0,因为e物品的重量是4,背包装不了。
对于d2单元格,表示只有物品e,d时,承重为2的背包,所能装入的最大价值仍然是0,因为物品e,d都不是这个背包能装的。
同理,c2=0,b2=3,a2=6。
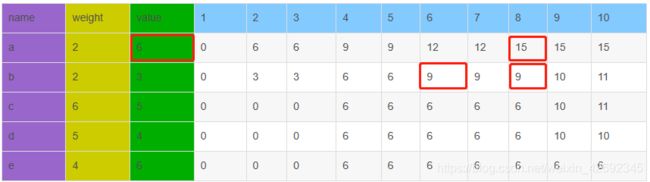
对于承重为8的背包,a8=15,是怎么得出的呢?
根据01背包的状态转换方程:
- 一个是
dp[i-1,j],对于这个例子来说就是b8=9,表示我有一个承重为8的背包,当只有物品b,c,d,e四件可选时,这个背包能装入的最大价值 dp[i-1][j-weight[i]]就是指单元格b6=9,表示我有一个承重为6的背包(8-2=6)(等于当前背包承重减去物品a的重量),当只有物品b,c,d,e四件可选时,这个背包能装入的最大价值value[i]指的是a物品的价值,即6- 由于
dp[i-1][j-weight[i]]+value[i] = 9+6 = 15大于dp[i-1][j] = 9,所以物品a应该放入承重为8的背包
② 求出背包中装入物品的编号
这里我们采用逆推的思路来处理,如果对于dp[i][j]>dp[i-1][j],则说明第i个物品肯定被放入了背包,此时我们再考察dp[i-1][j-weight[i]]的编号就可以了。
二维dp代码实现
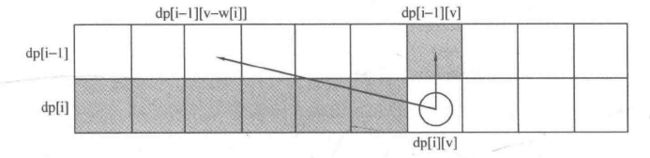
二维dp状态转移方程为:dp[i][j] = Max { dp[i-1][j] , dp[i-1][j-weight[i]] + value[i] }
由图可知,递推顺序是正序
/**
* 0-1背包问题
* @param V 背包容量
* @param N 物品种类
* @param weight 物品重量
* @param value 物品价值
* @return
*/
private static String ZeroOnePack(int V, int N, int[] weight, int[] value) {
int[][] dp = new int[N+1][V+1];
//为了便于理解, 将dp[i][0]和dp[0][j]均置为0, 从1开始计算
for(int i=1; i<=N; i++){
for(int j=1; j<=V; j++){
//如果第i件物品的重量大于背包容量j, 则不装入背包
//由于weight和value数组下标都是从0开始, 故第i个物品的重量为weight[i-1], 价值为value[i-1]
if(weight[i-1] > j)
dp[i][j] = dp[i-1][j];
else
dp[i][j] = Math.max(dp[i-1][j], dp[i-1][j-weight[i-1]]+value[i-1]);
}
}
//则容量为V的背包能够装入物品的最大值为
int maxValue = dp[N][V];
//逆推找出装入背包的所有商品的编号, 即在weight数组中的下标
int j=V;
String numStr="";
for(int i=N; i>0; i--){
//若果dp[i][j]>dp[i-1][j], 说明第i件物品是放入背包的
if(dp[i][j]>dp[i-1][j]){
numStr = i+" "+numStr;
j=j-weight[i-1];
}
if(j==0)
break;
}
return numStr;
}
二维动态规划
- 时间效率为
O(N*V) - 由于用到二维数组存储子问题的解,所以动态规划的空间效率为
O(N*V)
一维dp代码实现(滚动数组)
二维dp状态转移方程为:dp[i][j] = Max { dp[i-1][j] , dp[i-1][j-weight[i]] + value[i] }
一维dp状态转移方程为:dp[j] = Max { dp[j-weight[i]] + value[i], dp[j]) }
不同于二维dp的双重循环,空间优化版本的内层循环必须是逆序的
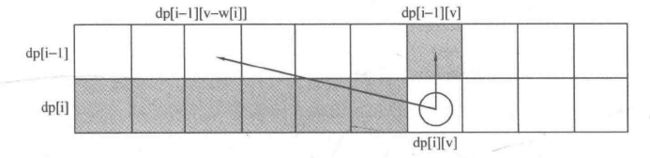
还是拿这张图说事
先说二维
每次更新dp[i][]时(第i层),只需用到dp[i-1][]的数据(第i-1层)。
具体的,更新dp[i][v]时,需要用到左上方dp[i-1][v-w[i]]和正上方dp[i-1][v]。
所以外层循环是物品种类,内层循环是背包容量。
一维dp
由于更新第i层的dp只需要用到第i-1层的数据,只需要维护一维dp,每次层数i变化时都重新更新dp【滚动数组】
外层循环是物品种类,内层循环背包容量必须逆序。
/**
* 思路:
* 只用一个一维数组记录状态,dp[i]表示容量为i的背包所能装入物品的最大价值
* 用逆序来实现
*/
private static int ZeroOnePack2(int V, int N, int[] weight, int[] value) {
int[] dp = new int[V+1];
for(int i=1; i<=N; i++) {
//逆序实现
for(int j=V; j>=weight[i-1]; j--) {
dp[j] = Math.max(dp[j-weight[i-1]]+value[i-1], dp[j]);
}
}
return dp[V];
}
贪心算法,无法全局最优
0-1 背包问题,运用贪婪算法去解决,无法达到全局最优。
有三种策略:
- 选取价值最大的物品
- 选择重量最轻的物品
- 选取价值/重量比最大的物品
策略1:每次尽可能选择价值最大的,行不通。举例说明如下。
物品有:ABC
重量分别是:25,10,10
价值分别是:100,80,80
根据策略,首先选取物品A,接下来就不能再去选其他物品,但是,如果选取 B 和 C,结果会更好。
策略 2:每次尽可能选择轻的物品,行不通。举例说明如下。
物品有:A B C
重量分别为:25, 10, 10
价值分别为:100, 5, 5
根据策略,首先选取物品 B 和 C,接下来就不能选 A,但是,如果选 A,价值更大。
策略 3:每次尽可能选价值/重量比最大的,行不通。举例说明如下。
物品有:A B C
重量是:25, 10, 10
价值是:25, 10, 10
根据策略,三种物品的价值/重量比都是一样,如果选 A,答案不对,应该选 B 和 C。
由上,贪婪算法总是做出在当前看来是最好的选择。即,它不从整体的角度去考虑,仅仅对局部的最优解感兴趣。因此,只有当那些局部最优策略能产生全局最优策略的时候,才能用贪婪算法。
多重背包
注意:考虑物品的件数限制时,需要取nums[i-1]和j/weight[i-1])的较小值
private static String manyPack(int V, int N, int[] weight, int[] value, int[] num) {
//初始化动态规划数组
int[][] dp = new int[N+1][V+1];
//为了便于理解, 将dp[i][0]和dp[0][j]均置为0, 从1开始计算
for(int i=1; i<=N; i++) {
for(int j=1; j<=V; j++) {
//如果第i件物品的重量大于背包容量j, 则不装入背包
//由于weight和value数组下标都是从0开始, 故第i个物品的重量为weight[i-1], 价值为value[i-1]
if(weight[i-1] > j)
dp[i][j] = dp[i-1][j];
else{
//考虑物品的件数限制
int maxV = Math.min(num[i-1], j/weight[i-1]);
for(int k=0; k<=maxV; k++) {
dp[i][j]=Math.max(dp[i-1][j], dp[i-1][j-k*weight[i-1]]+k*value[i-1]);
}
}
}
}
//则容量为V的背包能够装入物品的最大值为
int maxValue = dp[N][V];
int j=V;
String numStr="";
for(int i=N; i>0; i--) {
//若果dp[i][j]>dp[i-1][j],这说明第i件物品是放入背包的
while(dp[i][j]>dp[i-1][j]){
numStr = i+" "+numStr;
j=j-weight[i-1];
}
if(j==0)
break;
}
return numStr;
}
完全背包
思路分析:
- 01背包问题是在前一个子问题(
i-1种物品)的基础上来解决当前问题(i种物品),向i-1种物品时的背包添加第i种物品; - 而完全背包问题是在解决当前问题(
i种物品),向i种物品时的背包添加第i种物品。
01背包的状态转移方程为:dp[i][j] = Max { dp[i-1][j] , dp[i-1][j-weight[i]] + value[i] }
完全背包的状态转移方程为:dp[i][j] = Max { dp[i-1][j] , dp[i][j-weight[i]] + value[i] }
注意这里当考虑放入一个物品 i 时应当考虑还可能继续放入 i,
因此这里是dp[i][j-weight[i]]+value[i],而不是dp[i-1][j-weight[i]]+value[i]。
二维dp代码实现
private static String completePack(int V, int N, int[] weight, int[] value) {
//初始化动态规划数组
int[][] dp = new int[N+1][V+1];
//为了便于理解,将dp[i][0]和dp[0][j]均置为0,从1开始计算
for(int i=1; i<=N; i++) {
for(int j=1; j<=V; j++) {
//如果第i件物品的重量大于背包容量j,则不装入背包
//由于weight和value数组下标都是从0开始, 故第i个物品的重量为weight[i-1], 价值为value[i-1]
if(weight[i-1] > j)
dp[i][j] = dp[i-1][j];
else
dp[i][j] = Math.max(dp[i-1][j], dp[i][j-weight[i-1]]+value[i-1]);
}
}
//则容量为V的背包能够装入物品的最大值为
int maxValue = dp[N][V];
int j=V;
String numStr="";
for(int i=N; i>0; i--){
//若果dp[i][j]>dp[i-1][j], 这说明第i件物品是放入背包的
while(dp[i][j]>dp[i-1][j]){
numStr = i+" "+numStr;
j=j-weight[i-1];
}
if(j==0)
break;
}
return numStr;
}
一维dp代码实现
/**
* 思路:
* 只用一个一维数组记录状态,dp[i]表示容量为i的背包所能装入物品的最大价值
* 用顺序来实现
*/
private static int completePack2(int V, int N, int[] weight, int[] value){
//动态规划
int[] dp = new int[V+1];
for(int i=1; i<=N; i++){
//顺序实现
for(int j=weight[i-1]; j<=V; j++){
dp[j] = Math.max(dp[j-weight[i-1]]+value[i-1], dp[j]);
}
}
return dp[V];
}
便利蜂2020实习笔试第一题
贪心
import java.util.Arrays;
import java.util.Collections;
import java.util.Scanner;
public class Main {
public static void main(String[] args) {
Scanner sc = new Scanner(System.in);
int length = Integer.parseInt(sc.nextLine());
String [] widthsStr = sc.nextLine().split(",");
String [] valuesStr = sc.nextLine().split(",");
sc.close();
int n = widthsStr.length;
Commodity [] commodities = new Commodity[n];
for (int i=0; i<n; i++) {
Commodity commodity = new Commodity(
Integer.parseInt(widthsStr[i]),
Integer.parseInt(valuesStr[i]));
commodities[i] = commodity;
}
// 按单位重量价值从大到小排序
Arrays.sort(commodities, Collections.reverseOrder());
int ans = maxValue(commodities, n, length);
System.out.println(ans);
}
private static int maxValue(Commodity [] commodities, int n, int length) {
int tmpLength = length;
int maxValue = 0;
for (int i=0; i<n; i++) {
if (tmpLength - commodities[i].getWidth() < 0)
continue;
tmpLength -= commodities[i].getWidth();
maxValue += commodities[i].getValue();
}
return maxValue;
}
}
class Commodity implements Comparable<Commodity> {
private double width;
private double value;
private double unitValue;
public Commodity(double width, double value) {
this.width = width;
this.value = value;
this.unitValue = (width == 0) ? 0 : value / width;
}
public double getWidth() {
return width;
}
public void setWidth(double width) {
this.width = width;
}
public double getValue() {
return value;
}
public void setValue(double value) {
this.value = value;
}
public double getUnitValue() {
return unitValue;
}
public void setUnitValue(double unitValue) {
this.unitValue = unitValue;
}
@Override
public int compareTo(Commodity commodity) {
double value = commodity.unitValue;
if (unitValue > value)
return 1;
if (unitValue < value)
return -1;
return 0;
}
}
dp
import java.util.Scanner;
public class Main {
public static void main(String[] args) {
Scanner sc = new Scanner(System.in);
int length = Integer.parseInt(sc.nextLine());
String [] widthsStr = sc.nextLine().split(",");
String [] valuesStr = sc.nextLine().split(",");
sc.close();
int n = widthsStr.length;
int [] widths = new int[n];
int [] values = new int[n];
for (int i=0; i<n; i++) {
widths[i] = Integer.parseInt(widthsStr[i]);
values[i] = Integer.parseInt(valuesStr[i]);
}
int ans = maxValue(length, n, widths, values);
System.out.println(ans);
}
private static int maxValue(int length, int n, int[] widths, int[] values){
int [] dp = new int[length+1];
for(int i=1; i<n+1; i++) {
for(int j=length; j>=widths[i-1]; j--) {
dp[j] = Math.max(dp[j-widths[i-1]]+values[i-1], dp[j]);
}
}
return dp[length];
}
}
参考文章:
动态规划之01背包问题(最易理解的讲解)
经典算法总结——背包问题(java实现)【已完结】
贪心算法_01背包问题_Java实现