Leetcode刷题笔记——数据结构(双指针/快慢指针)
1.两数之和 II - 输入有序数组
原题:

思路:
最开始的思路不是双指针,简单的想两轮循环判断和。
class Solution {
public int[] twoSum(int[] numbers, int target) {
for(int i=0;i<numbers.length;i++){
for(int j=i+1;j<numbers.length;j++){
if(numbers[i]+numbers[j]==target)
return new int[] {i+1,j+1};
}
}
return null;
}
}
双指针的思路:
一边循环,头尾相加判断和,和大于目标值,则尾往前移,若是和小于目标值,则头往后移
class Solution {
public int[] twoSum(int[] numbers, int target) {
if(numbers==null)
return null;
int i=0,j=numbers.length-1;
int sum=0;
while(i<j){
sum=numbers[i]+numbers[j];
if(sum==target)
return new int[]{i+1,j+1};
else if(sum<target){
i++;
}
else{
j--;
}
}
return null;
}
}
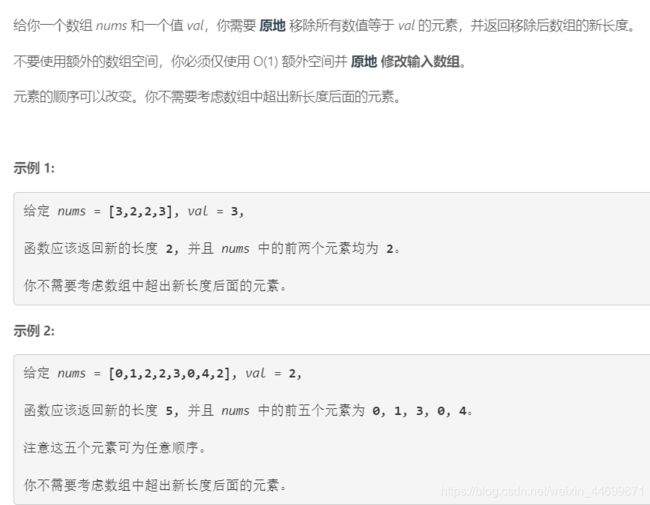
2.双指针之快慢指针
原题:
思路:
双指针,一个快指针指每个变动的元素,一个慢指针指不是val的值。
上代码:
class Solution {
public int removeElement(int[] nums, int val) {
int fast;
int slow=0;
for(fast=0;fast<nums.length;fast++){
if(nums[fast]!=val){
nums[slow]=nums[fast];
slow++;
}
}
return slow;
}
}
3. 最大连续1的个数
原题:

思路: 这里也是考虑双指针,一个指针是用来正常的遍历每一个元素,另一个指针是用来记录开始为1的索引的位置。连续1的数即这两个指针的差。然后用变量max来记录最大的连续为1的个数。
需要注意的是:
- slow指针原始值的设置,设置为-1,方便计算(主要是考虑如果第一个数为1的情况);二是为了下面这种情况
- 计算两个指针的差时,先要判断一下slow指针是不是不是-1,若不是-1,说明开始有1了。排除数组全是零的情况。
- 最后除了循环也要判断一下slow 的情况,这是考虑如果数组最后一个数也是1的情况。
上代码:
class Solution {
public int findMaxConsecutiveOnes(int[] nums) {
int fast=0;
int slow=-1;
int max=0;
for(;fast<nums.length;fast++){
if(nums[fast]==1){
if(slow==-1){
slow=fast;
}
}
else{
if(slow!=-1){
max=Math.max(max,fast-slow);
}
slow=-1;
}
}
if(slow!=-1)
max=Math.max(max,fast-slow);
return max;
}
}
4. 长度最小的子数组
原题
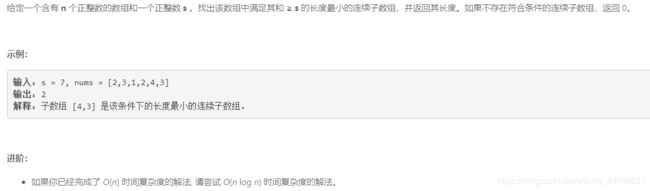
思路: 最先想到的是暴力破解,两遍循环,求和,然后判断一下是否大于等于s,并且用min储存最小长度。
PS:对min,还有max使用规范,初始化时
min=Integer.MAX_VALUE
max=Integer.MIN_VALUE
上代码:
class Solution {
public int minSubArrayLen(int s, int[] nums) {
int sum;
int min=Integer.MAX_VALUE;
boolean flag=false;
for(int j=0;j<nums.length;j++){
sum=nums[j];
if(sum>=s)
return 1;
for(int i=j+1;i<nums.length;i++){
sum+=nums[i];
if(sum>=s){
flag=true;
min=Math.min(min,i-j+1);
break;
}
}
}
if(flag==false)
return 0;
return min;
}
}
其他解法:
队列法: 类似于滑动窗口。数据先进入队列,相加求和,如果和大于等于s,则先不进数据,并且依次将先进的数据移出,每次移出的时候判断和是否大于等于s,并用min记录下队列中的数据个数。等到和小于s,后面的数据再依次进入队列。并且,这里采用的是头指针和尾指针来控制。
上代码:
class Solution {
public int minSubArrayLen(int s, int[] nums) {
int head=0;
int wei=0;
int sum=0;
int min=Integer.MAX_VALUE;
while(head<nums.length){
sum+=nums[head];
head++;
while(sum>=s){
min=Math.min(min,head-wei);
sum-=nums[wei];
wei++;
}
}
return min==Integer.MAX_VALUE?0:min;
}
}
PS:return min==Integer.MAX_VALUE?0:min;
这一句可以直接判断min并返回。简练!
5.删除排序数组中的重复项
原题:
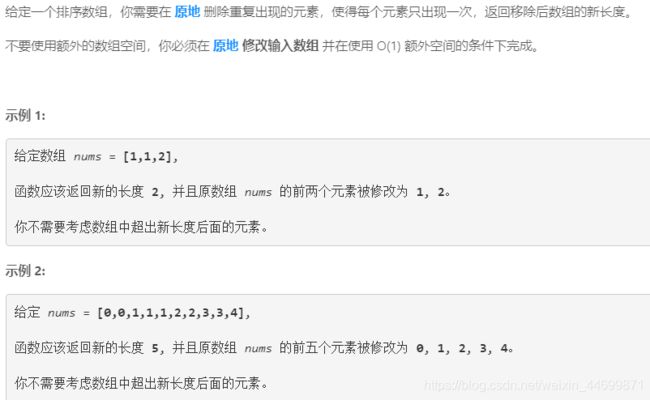
思路: 这里需要注意的是需要空间复杂度为O(1)。这里就排除了使用链表的可能。所以考虑使用快慢指针,用慢指针来指不重复的元素,用快指针来遍历。
上代码:
class Solution {
public int removeDuplicates(int[] nums) {
int i=0,j=0;
while(j<nums.length){
if(nums[i]==nums[j]){
j++;
}
else{
nums[++i]=nums[j];
j++;
}
}
return i+1;
}
}
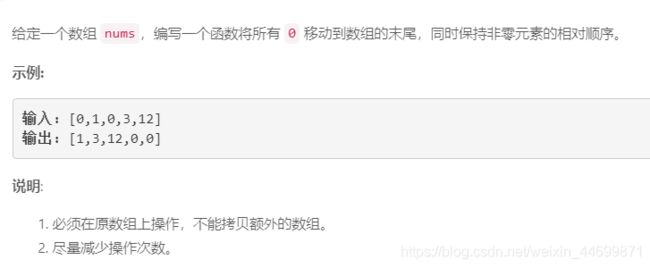
6.移动零
原题:
方法一:遍历一次
以快排的思想为基础,即考虑一个中间点,将数组中不为零的数放在中间点的左边,数组中的零放在中间点的右边,其中,中间点选为0。
其中,用慢指针记录零的位置,用快指针进行遍历。
上代码:
class Solution {
public void moveZeroes(int[] nums) {
int i=0;
for(int j=0;j<nums.length;j++){
if(nums[j]!=0){
int tem=nums[j];
nums[j]=nums[i];
nums[i]=tem;
i++;
}
}
}
}
方法二 遍历两次
也是双指针,快慢指针的思路。
第一次遍历时,用快指针遍历,用慢指针记录非零的元素,即,在遍历的过程中,遇到不为零的数就往左移动。最终慢指针留存的是移动后,数组中不为零的最后一个元素的位置。
第二次遍历,从慢指针记录的下一个位置起,对数组中剩余的元素进行清零。
上代码:
class Solution {
public void moveZeroes(int[] nums) {
if(nums==null) {
return;
}
//第一次遍历的时候,j指针记录非0的个数,只要是非0的统统都赋给nums[j]
int j = 0;
for(int i=0;i<nums.length;++i) {
if(nums[i]!=0) {
nums[j++] = nums[i];
}
}
//非0元素统计完了,剩下的都是0了
//所以第二次遍历把末尾的元素都赋为0即可
for(int i=j;i<nums.length;++i) {
nums[i] = 0;
}
}
}