【学习笔记】Pytorch深度学习—优化器(二)
【学习笔记】Pytorch深度学习—优化器(二)
- learning rate 学习率
- momentum 动量
- torch.optim.SGD
- Pytorch的十种优化器
前面学习过了Pytorch中优化器optimizer的基本属性和方法,优化器optimizer的主要功能是 “管理模型中的可学习参数,并利用参数的梯度grad以一定的策略进行更新”。本节内容分为4部分,(1)、(2)首先了解2个重要概念Learning rate学习率和momentum动量,(3)在此基础上,学习Pytorch中的SGD随机梯度下降优化器;(4)最后,了解Pytorch提供的十种优化器。
learning rate 学习率
上节课优化器(一)讲过梯度下降法的更新思路,也就是要求损失函数Loss或者参数朝着梯度的负方向去变化。为了更好的理解梯度下降法,下面给出一个例子。
引例:
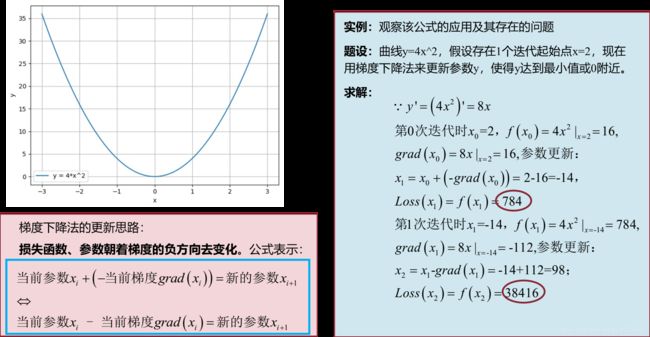
然而,从上面的例子中可以看出梯度下降法不仅没能使得y(或Loss值)降低至0甚至使得y变得更大了。
引例实验
代码演示梯度下降法全过程。
构造“损失函数”
绘制函数 y = 4 x 2 y=4x^2 y=4x2图像,该y值可类比为Loss值,梯度下降法的目的在于使得Loss值逐步降低至0。
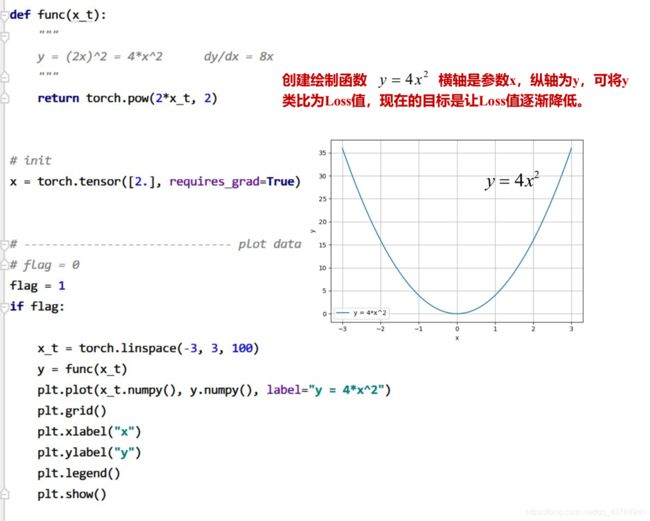
迭代更新部分
此外,当前梯度下降法公式还没有考虑到学习率lr的影响,因此下述实验学习率不设置即为lr=1,最大迭代参数为4。
# -------------- gradient descent -------------
flag = 1
if flag:
iter_rec, loss_rec, x_rec = list(), list(), list()
//当前公式还没有考虑学习率的影响,因此该参数lr设为 1
lr = 1 # /1. /.5 /.2 /.1 /.125
//迭代次数设为 4
max_iteration = 4 # /1. 4 /.5 4 /.2 20 200
for i in range(max_iteration):
//输入x 计算 Loss
y = func(x)
//反向传播计算梯度
y.backward()
print("Iter:{}, X:{:8}, X.grad:{:8}, loss:{:10}".format(
i, x.detach().numpy()[0], x.grad.detach().numpy()[0], y.item()))
x_rec.append(x.item())
//这里的x.data.sub_的 inplace操作可完成参数的更新
x.data.sub_(lr * x.grad) # x -= x.grad 数学表达式意义: x = x - x.grad # 0.5 0.2 0.1 0.125
//执行更新之后,对参数的梯度进行清零
x.grad.zero_()
iter_rec.append(i)
loss_rec.append(y)
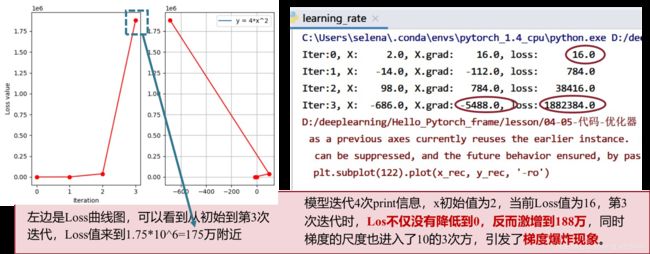
对损失函数使用梯度下降法的输出结果
从图3可以看出,迭代4次,Loss值不仅没有降低反而升高到了188万,同时最终参数x的梯度值也达到了 1 0 3 10^3 103,直接引发了梯度爆炸现象。
学习率
为什么使用了梯度下降法,Loss值并没有减小反而增大?
观察图1所示梯度下降法的求解过程,可以看出每次迭代时由于梯度grad()较大,从而引起新的参数变大进而导致Loss函数值不降反升,梯度爆炸等现象。因此,为了控制参数更新的步伐,就在原本的公式基础上引入了学习率LR,如下所示。
实验
依次设置学习率为0.5、0.2、0.1、0.125,观察Loss函数值及函数曲线变化情况
# ------------------ gradient descent -------------
flag = 1
if flag:
iter_rec, loss_rec, x_rec = list(), list(), list()
//当前公式还没有考虑学习率的影响,因此该参数lr设为 1
lr = 0.5 # /0.5 /0.2 /0.1 /0.125
//迭代次数设为 4
max_iteration = 4 # /1. 4 /.5 4 /.2 20 200
for i in range(max_iteration):
//输入x 计算 Loss
y = func(x)
//反向传播计算梯度
y.backward()
print("Iter:{}, X:{:8}, X.grad:{:8}, loss:{:10}".format(
i, x.detach().numpy()[0], x.grad.detach().numpy()[0], y.item()))
x_rec.append(x.item())
//这里的x.data.sub_的 inplace操作可完成参数的更新
x.data.sub_(lr * x.grad) # x -= x.grad 数学表达式意义: x = x - x.grad # 0.5 0.2 0.1 0.125
//执行更新之后,对参数的梯度进行清零
x.grad.zero_()
iter_rec.append(i)
loss_rec.append(y)
实验结果


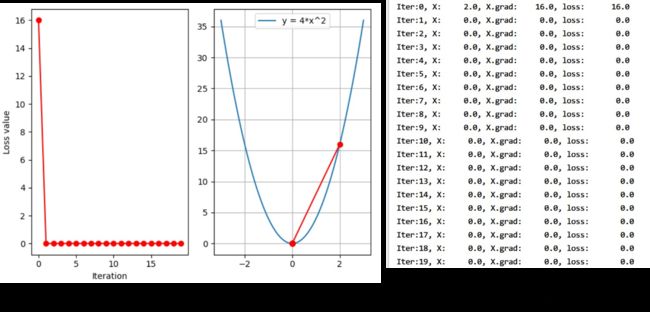
如果预先能知道损失函数Loss的函数表达式,就可以预先求得在学习率为0.125时,Loss就可以直接下降为0。但是通常,是不可能获得损失函数表达式的,因此0.125并不能直接求得。那么,该如何设置学习率呢?下面观察多个学习率之间Loss的变化情况。
多个学习率之间Loss变化情况
实验结果

< 总结 >
学习率
功能:用来控制更新的步伐
使用:设置学习率时,不能过大否则导致梯度爆炸、Loss值激增现象,也不能太小,这样就导致Loss值很难收敛。
通常设置为0.01.
学习率用来控制更新的步伐;在设置学习率时,不能过大比如0.5、0.3如图4(1)可能导致梯度爆炸、Loss值激增现象;学习率也不能太小,这样就导致Loss值很难收敛,进入收敛需要花费大量时间。
momentum 动量
在优化器中除了学习率还有momentum动量
Momentum(动量、冲量)
结合当前梯度与上一次更新信息,用于当前更新
< 预备知识 >
指数加权平均是在时间序列中经常使用的求取平均值的方法,其思想:求取当前时刻的平均值,距离当前时刻越近的参数值参考性越大,所占的权重也就越大,这些权重随着时间间隔增大是成指数下降的。
如下图5所示讨论了指数加权平均的计算原理,根据一温度散点图,列写了其计算式。
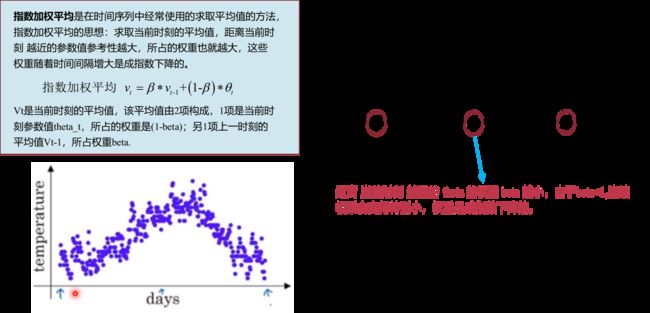

由于 β \beta β控制着权重的记忆周期, β \beta β值越小,记忆周期越长,作用越远;通常,会设置beta=0.9,beta=0.9的物理意义是更加关注当前时刻10天左右的数据。( 1 ( 1 − β ) = 1 1 − 0.9 = 10 \frac{1}{(1-\beta)}=\frac{1}{1-0.9}=10 (1−β)1=1−0.91=10)
通过上述例子,了解到指数加权平均中具有1个非常重要的参数 β \beta β,该 β \beta β对应到梯度下降中就是momentum系数。
< momentum加入,随机梯度下降公式更新 >
了解了momentum系数,下面就给出Pytorch中加入了momentum系数后,随机梯度下降中更新公式:
①仅考虑学习率的梯度下降:
w i + 1 = w i − l r ∗ g ( w i ) w_{i+1}=w_i-lr*g(w_i) wi+1=wi−lr∗g(wi)
②加入momentum系数后随机梯度下降更新公式:
v i = m ∗ v i − 1 + ∗ g ( w i ) v_{i}=m*v_{i-1}+*g(w_i) vi=m∗vi−1+∗g(wi) w i + 1 = w i + l r ∗ v i w_{i+1}=w_i+lr*v_{i} wi+1=wi+lr∗vi
w i + 1 w_{i+1} wi+1:第i+1次更新的参数; l r lr lr:学习率; v i v_i vi:更新量, m m m:momentum系数,对应指数加权平均就是 β \beta β值; g ( w i ) g(w_i) g(wi): w i 的 梯 度 w_i的梯度 wi的梯度
更新公式不再乘以梯度而是更新量 v i v_i vi,该更新量 v i v_i vi由两部分构成,不仅有当前的梯度信息 g ( w i ) g(w_i) g(wi)还有上一时刻的更新信息。
<更新公式实验>
下面进行带上momentum的随机梯度下降实验,观察Loss的变化。具体操作是:观察1个较小学习率0.01和1个较大学习率0.03 和 其中1个加了momentum后,观察两种情况下的Loss曲线。
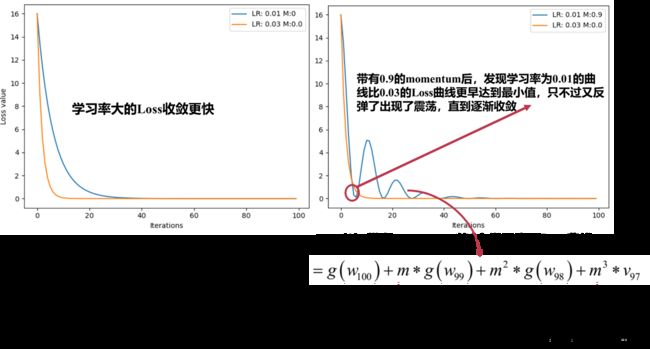

最后,尝试了多次momentum,直到momentum=0.63时,学习率为0.01的Loss比学习率为0.03的Loss更快收敛。设置合适mometum系数,考虑当前梯度信息结合之前的梯度信息,可以加速更新模型参数。
Momentum(动量、冲量)
结合当前梯度与上一次更新信息,用于当前参数,从而实现惯性思想,加速模型收敛。
torch.optim.SGD
Pytorch中提供的最常用、实用的优化器SGD
optim.SGD(params,lr=解释
(1)params(optimizer属性param_groups):管理的参数组参数组是1个list,其中的每1个元素是dict,dict中又很多key,这些key中最重要的是params——其中的value就是管理的参数;
(2)weight_decay:用来设置L2正则化系数;
(3)nesterov:布尔变量,通常设置为False,控制是否采用NAG这一梯度下降方法,参考 《 On the importance of initialization and momentum in deep learning》
Pytorch的十种优化器
1、optim.SGD:随机梯度下降法
2、optim.Adagrad:自适应学习率梯度下降法(对每个可学习参数具有1个自适应学习率)
3、optim.RMSprop:Adagrad的改进
4、optim.Adadelta:Adagrad的改进
5、optim.Adam:RMSprop结合Momentum
6、optim.Adamax:Adam增加学习率上限
7、optim.SparseAdam:稀疏版Adam
8、optim.ASGD:随机平均梯度下降
9、optim.Rprop:弹性反向传播(优化器应用场景在所有样本full_batch 一起计算梯度)
10、optim.LBFGS:BFGS的改进

PS:大部分任务的模型都可以采用SGD优化,其次,Adam优化器也比较常用,Adam优化器可以使用较大的学习率。