决策树

决策树作为监督学习类应用及其广泛的一类模型，既可以做分类又可以做回归，而决策树模型也在不断改进之中，首先介绍ID3算法，ID3算法的核心就是先对整个数据集进行总信息熵的计算，再对各个特征分别计算他们的信息熵，从而计算出信息增益，选择信息增益最大的特征进行分支，这就是贪心算法，所有的树模型都是运用了贪心算法

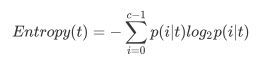
C4.5算法引入了分支度的概念，计算公式如下：

在C4.5算法中，使用之前得到的信息增益除以分支度作为选取切分字段的参考指标，就是增益率：

在C4.5中增加了针对连续变量的处理手段，首先将该列特征从小到大进行排序，对相邻两个数的中间数作为切分数据集的备选点，若一个特征具有N个值，那么C4.5的处理过程中就会产生N-1个切分点，再根据GR选择最优的切分点。

Cart树就是递归的构建二叉树的过程，对回归树使用平方误差最小化准则，对分类树用GINI系数作为指标
c4.5决策树代码 不含剪枝

import numpy as np
import pandas as pd
import random

def creatDataSet():
    group=np.array([[1,2],
                    [1,0],
                    [2,1],
                    [0,1],
                    [0,0]])
    labels=np.array([0,1,0,1,0])
    dataSet=pd.concat([pd.DataFrame(group),pd.DataFrame(labels)],axis=1,ignore_index=True)
    return dataSet

def clError(dataSet):
    m=dataSet.shape[0]
    iMax=dataSet.iloc[:,-1].value_counts(ascending=False)[0]
    return 1-iMax/m

def Ent(dataSet):
    m=dataSet.shape[0]
    iSet=dataSet.iloc[:,-1].value_counts()
    p=iSet/m
    Ent=(-p*np.log2(p)).sum()
    return Ent

def Gini(dataSet):
    m=dataSet.shape[0]
    iSet=dataSet.iloc[:,-1].value_counts()
    p=iSet/m
    Gini=1-(np.power(p,2)).sum()
    return Gini

def randSplit(dataSet,rate):
    l=list(dataSet.index)
    random.shuffle(l)
    dataSet.index=l
    n=dataSet.shape[0]
    m=int(n*rate)
    train=dataSet.loc[range(m),:]
    test=dataSet.loc[range(m,n),:]
    dataSet.index=range(dataSet.shape[0])
    test.index=range(test.shape[0])
    return train,test

def accuractCalculation(dataSet):
    m=dataSet.shape[0]
    res=(dataSet.iloc[:,-1]==dataSet.iloc[:,-2]).value_counts()
    acc=res.loc[True]/m
    print('accuracy is {}'.format(acc))
    return acc

def randSplit_1(dataSet,n):
    l=list(dataSet.index)
    random.shuffle(l)
    dataSet.index=l
    m=dataSet.shape[0]
    k=m/n
    splitSet=[]
    for i in range(n):
        if i< n-1:
            splitSet.append(dataSet.loc[range(i*int(k),(i+1)*int(k)),:])
        else:
            splitSet.append(dataSet.loc[range(i*int(k),m),:])
    dataSet.index=range(dataSet.shape[0])
    return splitSet

def crossVali(dataSet,randSplit,n,k):
    sp=randSplit(dataSet,n)
    result=np.array([])
    for i in range(n):
        test=sp[0]
        del sp[0]
        train=pd.concat(sp)
        train.index=range(train.shape[0])
        test.index=range(test.shape[0])
        test=classify(train,test,k)
        result=np.append(result,accuractCalculation(test))
        test=pd.DataFrame(test.drop(['predict'],axis=1))
        sp.append(test)
    return result,result.mean(),result.var()

def nodeSplit(dataSet):    
    m,n=dataSet.shape
    ent_fn=Ent(dataSet)
    treeNode=[dataSet]
    gr=np.array([])
    for i in pd.DataFrame(dataSet.iloc[:,:n-1]).columns:
        levels=dataSet.loc[:,i].value_counts(sort=False).index
        data_temp=[]
        ent_temp=[]
        iv_temp=np.array([])
        for j in levels:
            data_temp.append(dataSet[dataSet.loc[:,i]==j])
        for k in data_temp:
            ent_temp.append(Ent(k)*k.shape[0]/m)
            iv_temp=np.append(iv_temp,k.shape[0]/m)
        gn=ent_fn-sum(ent_temp)
        iv=(-iv_temp * np.log2(iv_temp)).sum()
        gr=np.append(gr,gn/iv)
    col_index=np.where(gr==gr.max())[0][0]
    levels=dataSet.iloc[:,col_index].value_counts(sort=False).index
    data_temp=[]
    for j in levels:
        data_temp.append(dataSet[dataSet.iloc[:,col_index]==j])
    for z in data_temp:
        del z[z.columns[col_index]]
    return gr,data_temp

def treeGrowth(dataSet):
    m,n=dataSet.shape
    treeNode=[dataSet]
    der=True
    while der:
        len_b=len(treeNode)
        for i in range(len_b):
            if treeNode[i].shape[1]>1:
                gr,data_temp=nodeSplit(treeNode[i])
            if gr.min()>0:
                del(treeNode[i])
                treeNode.extend(data_temp)
        len_a=len(treeNode)
        der=not(len_a==len_b)
    return treeNode