CMU 11-785 L13 Recurrent Networks
Modelling Series
-
In many situations one must consider a series of inputs to produce an output
- Outputs too may be a series
-
Finite response model
-
Can use convolutional neural net applied to series data (slide)
- Also called a Time-Delay neural network
-
Something that happens today only affects the output of the system for days into the future
- Y t = f ( X t , X t − 1 , … , X t − N ) Y_{t}=f\left(X_{t}, X_{t-1}, \ldots, X_{t-N}\right) Yt=f(Xt,Xt−1,…,Xt−N)
-
-
Infinite response systems
-
Systems often have long-term dependencies
-
What happens today can continue to affect the output forever
- Y t = f ( X t , X t − 1 , … , X t − ∞ ) Y_{t}=f\left(X_{t}, X_{t-1}, \ldots, X_{t-\infty}\right) Yt=f(Xt,Xt−1,…,Xt−∞)
-
Infinite response systems
-
A one-tap NARX network
-
An explicit memory variable whose job it is to remember
- m t = r ( y t − 1 , h t − 1 ′ , m t − 1 ) h t = f ( x t , m t ) y t = g ( h t ) \begin{array}{c} m_{t}=r\left(y_{t-1}, h_{t-1}^{\prime}, m_{t-1}\right) \\\\ h_{t}=f\left(x_{t}, m_{t}\right) \\\\ y_{t}=g\left(h_{t}\right) \end{array} mt=r(yt−1,ht−1′,mt−1)ht=f(xt,mt)yt=g(ht)
-
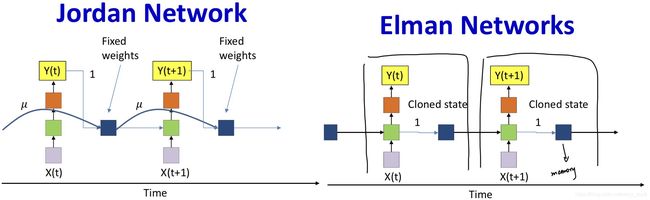
Jordan Network
- Memory unit simply retains a running average of past outputs
- Memory has fixed structure; does not “learn” to remember
-
Elman Networks
- Separate memory state from output
- Only the weight from the memory unit to the hidden unit is learned
- But during training no gradient is backpropagated over the “1” link (Just cloned state)
-
Problem
- “Simple” (or partially recurrent) because during learning current error does not actually propagate to the past
State-space model
h t = f ( x t , h t − 1 ) y t = g ( h t ) \begin{array}{c} h_{t}=f\left(x_{t}, h_{t-1}\right) \\\\ y_{t}=g\left(h_{t}\right) \end{array} ht=f(xt,ht−1)yt=g(ht)
- h t h_t ht is the state of the network
- Model directly embeds the memory in the state
- State summarizes information about the entire past
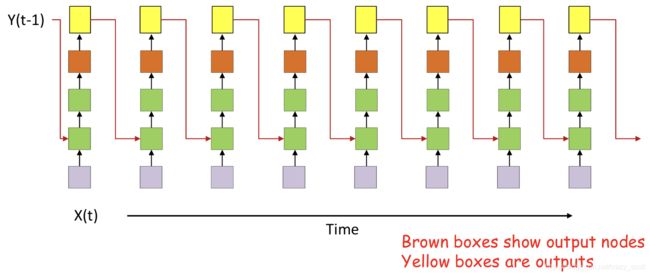
- Recurrent neural network
Variants
- All columns are identical
- The simplest structures are most popular
Recurrent neural network
Forward pass
Backward pass
- BPTT
- Back Propagation Through Time
- Defining a divergence between the actual and desired output sequences
- Backpropagating gradients over the entire chain of recursion
- Backpropagation through time
- Pooling gradients with respect to individual parameters over time
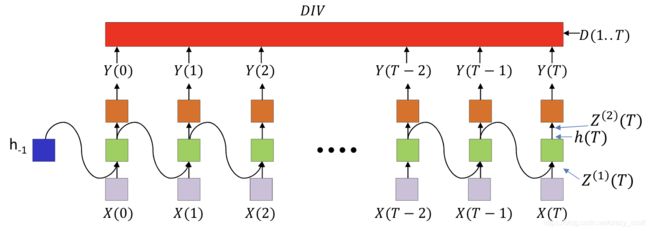
Notion
- The divergence computed is between the sequence of outputs by the network and the desired sequence of outputs
- DIV is a scalar function of a …series… of vectors
- This is not just the sum of the divergences at individual times
- Y ( t ) Y(t) Y(t) is the output at time t t t
- Y i ( t ) Y_i(t) Yi(t) is the ith output
- Z ( 2 ) ( t ) Z^{(2)}(t) Z(2)(t) is the pre-activation value of the neurons at the output layer at time t t t
- h ( t ) h(t) h(t) is the output of the hidden layer at time t t t
BPTT
- Y ( t ) Y(t) Y(t) is a column vector
- D I V DIV DIV is a scalar
- d D i v d Y ( t ) \frac{d Div}{d Y(t)} dY(t)dDiv is a row vector
Derivative at time T T T
-
Compute d D I V d Y i ( T ) \frac{d DIV}{d Y_i(T)} dYi(T)dDIV for all i i i
-
In general we will be required to compute d D I V d Y i ( t ) \frac{d DIV}{d Y_i(t)} dYi(t)dDIV for all i i i and t t t as we will see
- This can be a source of significant difficulty in many scenarios
-
Special case, when the overall divergence is a simple sum of local divergences at each time
- d D I V d Y i ( t ) = d D i v ( t ) d Y i ( t ) \frac{d D I V}{d Y_{i}(t)}=\frac{d D i v(t)}{d Y_{i}(t)} dYi(t)dDIV=dYi(t)dDiv(t)
-
-
Compute ∇ Z ( 2 ) ( T ) D I V \nabla_{Z^{(2)}(T)}{D I V} ∇Z(2)(T)DIV
-
∇ Z ( 2 ) ( T ) D I V = ∇ Y ( T ) D I V ∇ Z ( 2 ) ( T ) Y ( T ) \nabla_{Z^{(2)}(T)}{D I V}=\nabla_{Y(T)} D I V \nabla_{Z^{(2)}(T)} Y(T) ∇Z(2)(T)DIV=∇Y(T)DIV∇Z(2)(T)Y(T)
-
For scalar output activation
- d D I V d Z i ( 2 ) ( T ) = d D I V d Y i ( T ) d Y i ( T ) d Z i ( 2 ) ( T ) \frac{d D I V}{d Z_{i}^{(2)}(T)}=\frac{d D I V}{d Y_{i}(T)} \frac{d Y_{i}(T)}{d Z_{i}^{(2)}(T)} dZi(2)(T)dDIV=dYi(T)dDIVdZi(2)(T)dYi(T)
-
For vector output activation
- d D I V d Z i ( 2 ) ( T ) = ∑ i d D I V d Y j ( T ) d Y j ( T ) d Z i ( 2 ) ( T ) \frac{d D I V}{d Z_{i}^{(2)}(T)}=\sum_{i} \frac{d D I V}{d Y_{j}(T)} \frac{d Y_{j}(T)}{d Z_{i}^{(2)}(T)} dZi(2)(T)dDIV=i∑dYj(T)dDIVdZi(2)(T)dYj(T)
-
-
Compute ∇ h ( T ) D I V \nabla_{h_(T)}{D I V} ∇h(T)DIV
-
W ( 2 ) h ( T ) = Z ( 2 ) ( T ) W^{(2)} h(T) = Z^{(2)}(T) W(2)h(T)=Z(2)(T)
-
d D I V d h i ( T ) = ∑ j d D I V d Z j ( 2 ) ( T ) d Z j ( 2 ) ( T ) d h i ( T ) = ∑ j w i j ( 2 ) d D I V d Z j ( 2 ) ( T ) \frac{d D I V}{d h_{i}(T)}=\sum_{j} \frac{d D I V}{d Z_{j}^{(2)}(T)} \frac{d Z_{j}^{(2)}(T)}{d h_{i}(T)}=\sum_{j} w_{i j}^{(2)} \frac{d D I V}{d Z_{j}^{(2)}(T)} dhi(T)dDIV=j∑dZj(2)(T)dDIVdhi(T)dZj(2)(T)=j∑wij(2)dZj(2)(T)dDIV
-
∇ h ( T ) D I V = ∇ Z ( 2 ) ( T ) D I V W ( 2 ) \nabla_{h(T)} D I V=\nabla_{Z^{(2)}(T)} D I V W^{(2)} ∇h(T)DIV=∇Z(2)(T)DIVW(2)
-
-
Compute ∇ W ( 2 ) D I V \nabla_{W^{(2)}}{D I V} ∇W(2)DIV
-
d D I V d w i j ( 2 ) = d D I V d Z j ( 2 ) ( T ) h i ( T ) \frac{d D I V}{d w_{i j}^{(2)}}=\frac{d D I V}{d Z_{j}^{(2)}(T)} h_{i}(T) dwij(2)dDIV=dZj(2)(T)dDIVhi(T)
-
∇ W ( 2 ) D I V = h ( T ) ∇ Z ( 2 ) ( T ) D I V \nabla_{W^{(2)}} D I V=h(T) \nabla_{Z^{(2)}(T)} D I V ∇W(2)DIV=h(T)∇Z(2)(T)DIV
-
-
Compute ∇ Z ( 1 ) ( T ) D I V \nabla_{Z^{(1)}(T)}{D I V} ∇Z(1)(T)DIV
-
d D I V d Z i ( 1 ) ( T ) = d D I V d h i ( T ) d h i ( T ) d Z i ( 1 ) ( T ) \frac{d D I V}{d Z_{i}^{(1)}(T)}=\frac{d D I V}{d h_{i}(T)} \frac{d h_{i}(T)}{d Z_{i}^{(1)}(T)} dZi(1)(T)dDIV=dhi(T)dDIVdZi(1)(T)dhi(T)
-
∇ Z ( 1 ) ( T ) D I V = ∇ h ( T ) D I V ∇ Z ( 1 ) ( T ) h ( T ) \nabla_{Z^{(1)}(T)} D I V=\nabla_{h(T)} D I V \nabla_{Z^{(1)}(T)} h(T) ∇Z(1)(T)DIV=∇h(T)DIV∇Z(1)(T)h(T)
-
-
Compute ∇ W ( 1 ) D I V \nabla_{W^{(1)}}{D I V} ∇W(1)DIV
-
W ( 1 ) X ( T ) + W ( 11 ) h ( T − 1 ) = Z ( 1 ) ( T ) W^{(1)} X(T) + W^{(11)} h(T-1)= Z^{(1)}(T) W(1)X(T)+W(11)h(T−1)=Z(1)(T)
-
d D I V d w i j ( 1 ) = d D I V d Z j ( 1 ) ( T ) X i ( T ) \frac{d D I V}{d w_{i j}^{(1)}}=\frac{d D I V}{d Z_{j}^{(1)}(T)} X_{i}(T) dwij(1)dDIV=dZj(1)(T)dDIVXi(T)
-
∇ W ( 1 ) D I V = X ( T ) ∇ Z ( 1 ) ( T ) D I V \nabla_{W^{(1)}} D I V=X(T) \nabla_{Z^{(1)}(T)} D I V ∇W(1)DIV=X(T)∇Z(1)(T)DIV
-
-
Compute ∇ W ( 11 ) D I V \nabla_{W^{(11)}}{D I V} ∇W(11)DIV
-
d D I V d w i i ( 11 ) = d D I V d Z i ( 1 ) ( T ) h i ( T − 1 ) \frac{d D I V}{d w_{i i}^{(11)}}=\frac{d D I V}{d Z_{i}^{(1)}(T)} h_{i}(T-1) dwii(11)dDIV=dZi(1)(T)dDIVhi(T−1)
-
∇ W ( 11 ) D I V = h ( T − 1 ) ∇ Z ( 1 ) ( T ) D I V \nabla_{W}^{(11)} D I V=h(T-1) \nabla_{Z^{(1)}(T)} D I V ∇W(11)DIV=h(T−1)∇Z(1)(T)DIV
-
Derivative at time T − 1 T-1 T−1
-
Compute ∇ Z ( 2 ) ( T − 1 ) D I V \nabla_{Z^{(2)}(T-1)}{D I V} ∇Z(2)(T−1)DIV
-
∇ Z ( 2 ) ( T − 1 ) D I V = ∇ Y ( T − 1 ) D I V ∇ Z ( 2 ) ( T − 1 ) Y ( T − 1 ) \nabla_{Z^{(2)}(T-1)}{D I V}=\nabla_{Y(T-1)} D I V \nabla_{Z^{(2)}(T-1)} Y(T-1) ∇Z(2)(T−1)DIV=∇Y(T−1)DIV∇Z(2)(T−1)Y(T−1)
-
For scalar output activation
- d D I V d Z i ( 2 ) ( T − 1 ) = d D I V d Y i ( T − 1 ) d Y i ( T − 1 ) d Z i ( 2 ) ( T − 1 ) \frac{d D I V}{d Z_{i}^{(2)}(T-1)}=\frac{d D I V}{d Y_{i}(T-1)} \frac{d Y_{i}(T-1)}{d Z_{i}^{(2)}(T-1)} dZi(2)(T−1)dDIV=dYi(T−1)dDIVdZi(2)(T−1)dYi(T−1)
-
For vector output activation
- d D I V d Z i ( 2 ) ( T − 1 ) = ∑ j d D I V d Y j ( T − 1 ) d Y j ( T − 1 ) d Z i ( 2 ) ( T − 1 ) \frac{d D I V}{d Z_{i}^{(2)}(T-1)}=\sum_{j} \frac{d D I V}{d Y_{j}(T-1)} \frac{d Y_{j}(T-1)}{d Z_{i}^{(2)}(T-1)} dZi(2)(T−1)dDIV=j∑dYj(T−1)dDIVdZi(2)(T−1)dYj(T−1)
-
-
Compute ∇ h ( T − 1 ) D I V \nabla_{h_(T-1)}{D I V} ∇h(T−1)DIV
-
d D I V d h i ( T − 1 ) = ∑ j w i j ( 2 ) d D I V d Z j ( 2 ) ( T − 1 ) + ∑ j w i j ( 11 ) d D I V d Z j ( 1 ) ( T ) \frac{d D I V}{d h_{i}(T-1)}=\sum_{j} w_{i j}^{(2)} \frac{d D I V}{d Z_{j}^{(2)}(T-1)}+\sum_{j} w_{i j}^{(11)} \frac{d D I V}{d Z_{j}^{(1)}(T)} dhi(T−1)dDIV=j∑wij(2)dZj(2)(T−1)dDIV+j∑wij(11)dZj(1)(T)dDIV
-
∇ h ( T − 1 ) D I V = ∇ Z ( 2 ) ( T − 1 ) D I V W ( 2 ) + ∇ Z ( 1 ) ( T ) D I V W ( 11 ) \nabla_{h(T-1)} D I V=\nabla_{Z^{(2)}(T-1)} D I V W^{(2)}+\nabla_{Z^{(1)}(T)} D I V W^{(11)} ∇h(T−1)DIV=∇Z(2)(T−1)DIVW(2)+∇Z(1)(T)DIVW(11)
-
-
Compute ∇ W ( 2 ) D I V \nabla_{W^{(2)}}{D I V} ∇W(2)DIV
-
d D I V d w i j ( 2 ) + = d D I V d Z j ( 2 ) ( T − 1 ) h i ( T − 1 ) \frac{d D I V}{d w_{i j}^{(2)}}+=\frac{d D I V}{d Z_{j}^{(2)}(T-1)} h_{i}(T-1) dwij(2)dDIV+=dZj(2)(T−1)dDIVhi(T−1)
-
∇ W ( 2 ) D I V + = h ( T − 1 ) ∇ Z ( 2 ) ( T − 1 ) D I V \nabla_{W^{(2)}} D I V+=h(T-1) \nabla_{Z^{(2)}(T-1)} D I V ∇W(2)DIV+=h(T−1)∇Z(2)(T−1)DIV
-
-
Compute ∇ Z ( 1 ) ( T − 1 ) D I V \nabla_{Z^{(1)}(T-1)}{D I V} ∇Z(1)(T−1)DIV
-
d D I V d Z i ( 1 ) ( T − 1 ) = d D I V d h i ( T − 1 ) d h i ( T − 1 ) d Z i ( 1 ) ( T − 1 ) \frac{d D I V}{d Z_{i}^{(1)}(T-1)}=\frac{d D I V}{d h_{i}(T-1)} \frac{d h_{i}(T-1)}{d Z_{i}^{(1)}(T-1)} dZi(1)(T−1)dDIV=dhi(T−1)dDIVdZi(1)(T−1)dhi(T−1)
-
∇ Z ( 1 ) ( T − 1 ) D I V = ∇ h ( T − 1 ) D I V ∇ Z ( 1 ) ( T − 1 ) h ( T − 1 ) \nabla_{Z^{(1)}(T-1)} D I V=\nabla_{h(T-1)} D I V \nabla_{Z^{(1)}(T-1)} h(T-1) ∇Z(1)(T−1)DIV=∇h(T−1)DIV∇Z(1)(T−1)h(T−1)
-
-
Compute ∇ W ( 1 ) D I V \nabla_{W^{(1)}}{D I V} ∇W(1)DIV
-
d D I V d w i j ( 1 ) + = d D I V d Z j ( 1 ) ( T − 1 ) X i ( T − 1 ) \frac{d D I V}{d w_{i j}^{(1)}}+=\frac{d D I V}{d Z_{j}^{(1)}(T-1)} X_{i}(T-1) dwij(1)dDIV+=dZj(1)(T−1)dDIVXi(T−1)
-
∇ W ( 1 ) D I V + = X ( T − 1 ) ∇ Z ( 1 ) ( T − 1 ) D I V \nabla_{W^{(1)}} D I V+=X(T-1) \nabla_{Z^{(1)}(T-1)} D I V ∇W(1)DIV+=X(T−1)∇Z(1)(T−1)DIV
-
-
Compute ∇ W ( 11 ) D I V \nabla_{W^{(11)}}{D I V} ∇W(11)DIV
-
d D I V d w i j ( 11 ) + = d D I V d Z j ( 1 ) ( T − 1 ) h i ( T − 2 ) \frac{d D I V}{d w_{i j}^{(11)}}+=\frac{d D I V}{d Z_{j}^{(1)}(T-1)} h_{i}(T-2) dwij(11)dDIV+=dZj(1)(T−1)dDIVhi(T−2)
-
∇ W ( 11 ) D I V + = h ( T − 2 ) ∇ Z ( 1 ) ( T − 1 ) D I V \nabla_{W^{(11)}} D I V+=h(T-2) \nabla_{Z^{(1)}(T-1)} D I V ∇W(11)DIV+=h(T−2)∇Z(1)(T−1)DIV
-
Back Propagation Through Time
d D I V d h i ( − 1 ) = ∑ i w i j ( 11 ) d D I V d Z j ( 1 ) ( 0 ) \frac{d D I V}{d h_{i}(-1)}=\sum_{i} w_{i j}^{(11)} \frac{d D I V}{d Z_{j}^{(1)}(0)} dhi(−1)dDIV=i∑wij(11)dZj(1)(0)dDIV
d D I V d h i ( k ) ( t ) = ∑ j w i , j ( k + 1 ) d D I V d Z j ( k + 1 ) ( t ) + ∑ j w i , j ( k , k ) d D I V d Z j ( k ) ( t + 1 ) \frac{d D I V}{d h_{i}^{(k)}(t)}=\sum_{j} w_{i, j}^{(k+1)} \frac{d D I V}{d Z_{j}^{(k+1)}(t)}+\sum_{j} w_{i, j}^{(k, k)} \frac{d D I V}{d Z_{j}^{(k)}(t+1)} dhi(k)(t)dDIV=j∑wi,j(k+1)dZj(k+1)(t)dDIV+j∑wi,j(k,k)dZj(k)(t+1)dDIV
d D I V d Z i ( k ) ( t ) = d D I V d h i ( k ) ( t ) f k ′ ( Z i ( k ) ( t ) ) \frac{d D I V}{d Z_{i}^{(k)}(t)}=\frac{d D I V}{d h_{i}^{(k)}(t)} f_{k}^{\prime}\left(Z_{i}^{(k)}(t)\right) dZi(k)(t)dDIV=dhi(k)(t)dDIVfk′(Zi(k)(t))
d D I V d w i j ( 1 ) = ∑ t d D I V d Z j ( 1 ) ( t ) X i ( t ) \frac{d D I V}{d w_{i j}^{(1)}}=\sum_{t} \frac{d D I V}{d Z_{j}^{(1)}(t)} X_{i}(t) dwij(1)dDIV=t∑dZj(1)(t)dDIVXi(t)
d D I V d w i j ( 11 ) = ∑ t d D I V d Z j ( 1 ) ( t ) h i ( t − 1 ) \frac{d D I V}{d w_{i j}^{(11)}}=\sum_{t} \frac{d D I V}{d Z_{j}^{(1)}(t)} h_{i}(t-1) dwij(11)dDIV=t∑dZj(1)(t)dDIVhi(t−1)
Algorithm
Bidirectional RNN
- Two independent RNN
- Clearly, this is not an online process and requires the entire input data
- It is easy to learning two RNN independently
- Forward pass: Compute both forward and backward networks and final output
- Backpropagation
- A basic backprop routine that we will call
- Two calls to the routine within a higher-level wrapper