动手学深度学习(PyTorch实现)(十二)--批量归一化（BatchNormalization）

1. 前言

本博文理论部分摘自CSDN博主「Paulzhao6518」的文章《（BN）批量归一化全面解析》。

先来思考一个问题：我们知道在神经网络训练开始前，都要对输入数据做一个归一化处理，那么具体为什么需要归一化呢？归一化后有什么好处呢？原因在于神经网络学习过程本质就是为了学习数据分布，一旦训练数据与测试数据的分布不同，那么网络的泛化能力也大大降低；另外一方面，一旦每批训练数据的分布各不相同(batch 梯度下降)，那么网络就要在每次迭代都去学习适应不同的分布，这样将会大大降低网络的训练速度，这也正是为什么我们需要对数据都要做一个归一化预处理的原因。

对于深度网络的训练是一个复杂的过程，只要网络的前面几层发生微小的改变，那么后面几层就会被累积放大下去。一旦网络某一层的输入数据的分布发生改变，那么这一层网络就需要去适应学习这个新的数据分布，所以如果训练过程中，训练数据的分布一直在发生变化，那么将会影响网络的训练速度。

我们知道网络一旦train起来，那么参数就要发生更新，除了输入层的数据外(因为输入层数据，我们已经人为的为每个样本归一化)，后面网络每一层的输入数据分布是一直在发生变化的，因为在训练的时候，前面层训练参数的更新将导致后面层输入数据分布的变化。以网络第二层为例：网络的第二层输入，是由第一层的参数和input计算得到的，而第一层的参数在整个训练过程中一直在变化，因此必然会引起后面每一层输入数据分布的改变。我们把网络中间层在训练过程中，数据分布的改变称之为：“Internal Covariate Shift”。Paper所提出的算法，就是要解决在训练过程中，中间层数据分布发生改变的情况，于是就有了Batch Normalization，这个牛逼算法的诞生。

2. 批量归一化的优势

BN算法（Batch Normalization）其强大之处如下：

• 可以选择比较大的初始学习率，让训练速度飙涨。以前还需要慢慢调整学习率，甚至在网络训练到一半的时候，还需要想着学习率进一步调小的比例选择多少比较合适，现在我们可以采用初始很大的学习率，然后学习率的衰减速度也很大，因为这个算法收敛很快。当然这个算法即使你选择了较小的学习率，也比以前的收敛速度快，因为它具有快速训练收敛的特性；

• 不用去担心过拟合中drop out、L2正则项参数的选择问题，采用BN算法后，你可以移除这两项了参数，或者可以选择更小的L2正则约束参数了，因为BN具有提高网络泛化能力的特性；

• 不需要使用使用局部响应归一化层了（局部响应归一化是Alexnet网络用到的方法，搞视觉的估计比较熟悉），因为BN本身就是一个归一化网络层；

• 可以把训练数据彻底打乱（防止每批训练的时候，某一个样本都经常被挑选到）

3. BN算法介绍

就像激活函数层、卷积层、全连接层、池化层一样，BN(Batch Normalization)也属于网络的一层。在前面我们提到网络除了输出层外，其它层因为低层网络在训练的时候更新了参数，而引起后面层输入数据分布的变化。这个时候我们可能就会想，如果在每一层输入的时候，再加个预处理操作那该有多好啊，比如网络第三层输入数据X3(X3表示网络第三层的输入数据)把它归一化至：均值0、方差为1，然后再输入第三层计算，这样我们就可以解决前面所提到的“Internal Covariate Shift”的问题了。

实现BN并不是那么简单的。如果是仅仅使用普通的归一化公式，对网络某一层A的输出数据做归一化，然后送入网络下一层B，这样是会影响到本层网络A所学习到的特征的。打个比方，比如我网络中间某一层学习到特征数据本身就分布在S型激活函数的两侧，你强制进行归一化处理、标准差也限制在了1，把数据变换成分布于s函数的中间部分，这样就相当于我这一层网络所学习到的特征分布被你搞坏了，这可怎么办？于是BN算法是怎么做的：变换重构，引入了可学习参数γ、β，这就是算法关键之处：

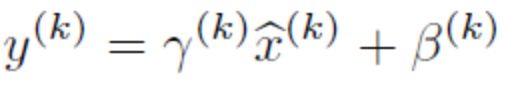
每一个神经元xk都会有一对这样的参数γ、β。这样其实当：

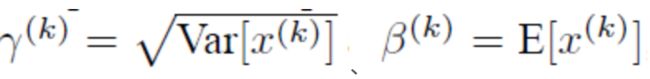
是可以恢复出原始的某一层所学到的特征的。因此我们引入了这个可学习重构参数γ、β，让我们的网络可以学习恢复出原始网络所要学习的特征分布。最后Batch Normalization网络层的前向传导过程公式就是：

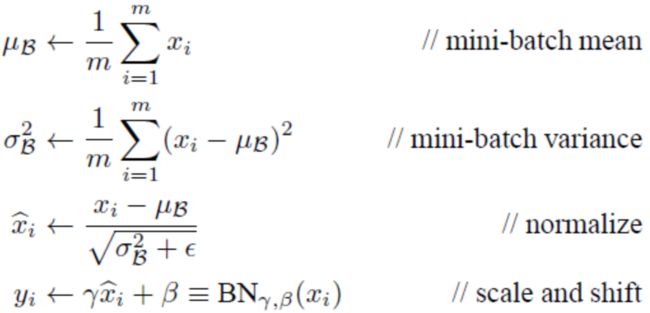
4. PyTorch实现

4.1 导入相应的包

import time
import torch
from torch import nn, optim
import torch.nn.functional as F
import torchvision
import sys
sys.path.append("/home/kesci/input/") 
import d2lzh1981 as d2l
device = torch.device('cuda' if torch.cuda.is_available() else 'cpu')

4.2 定义BN函数

def batch_norm(is_training, X, gamma, beta, moving_mean, moving_var, eps, momentum):
    # 判断当前模式是训练模式还是预测模式
    if not is_training:
        # 如果是在预测模式下，直接使用传入的移动平均所得的均值和方差
        X_hat = (X - moving_mean) / torch.sqrt(moving_var + eps)
    else:
        assert len(X.shape) in (2, 4)
        if len(X.shape) == 2:
            # 使用全连接层的情况，计算特征维上的均值和方差
            mean = X.mean(dim=0)
            var = ((X - mean) ** 2).mean(dim=0)
        else:
            # 使用二维卷积层的情况，计算通道维上（axis=1）的均值和方差。这里我们需要保持
            # X的形状以便后面可以做广播运算
            mean = X.mean(dim=0, keepdim=True).mean(dim=2, keepdim=True).mean(dim=3, keepdim=True)
            var = ((X - mean) ** 2).mean(dim=0, keepdim=True).mean(dim=2, keepdim=True).mean(dim=3, keepdim=True)
        # 训练模式下用当前的均值和方差做标准化
        X_hat = (X - mean) / torch.sqrt(var + eps)
        # 更新移动平均的均值和方差
        moving_mean = momentum * moving_mean + (1.0 - momentum) * mean
        moving_var = momentum * moving_var + (1.0 - momentum) * var
    Y = gamma * X_hat + beta  # 拉伸和偏移
    return Y, moving_mean, moving_var

4.3 定义BN类

class BatchNorm(nn.Module):
    def __init__(self, num_features, num_dims):
        super(BatchNorm, self).__init__()
        if num_dims == 2:
            shape = (1, num_features) #全连接层输出神经元
        else:
            shape = (1, num_features, 1, 1)  #通道数
        # 参与求梯度和迭代的拉伸和偏移参数，分别初始化成0和1
        self.gamma = nn.Parameter(torch.ones(shape))
        self.beta = nn.Parameter(torch.zeros(shape))
        # 不参与求梯度和迭代的变量，全在内存上初始化成0
        self.moving_mean = torch.zeros(shape)
        self.moving_var = torch.zeros(shape)

    def forward(self, X):
        # 如果X不在内存上，将moving_mean和moving_var复制到X所在显存上
        if self.moving_mean.device != X.device:
            self.moving_mean = self.moving_mean.to(X.device)
            self.moving_var = self.moving_var.to(X.device)
        # 保存更新过的moving_mean和moving_var, Module实例的traning属性默认为true, 调用.eval()后设成false
        Y, self.moving_mean, self.moving_var = batch_norm(self.training, 
            X, self.gamma, self.beta, self.moving_mean,
            self.moving_var, eps=1e-5, momentum=0.9)
        return Y

5. 基于LeNet的应用

5.1 定义LeNet

net = nn.Sequential(
            nn.Conv2d(1, 6, 5), # in_channels, out_channels, kernel_size
            BatchNorm(6, num_dims=4),
            nn.Sigmoid(),
            nn.MaxPool2d(2, 2), # kernel_size, stride
            nn.Conv2d(6, 16, 5),
            BatchNorm(16, num_dims=4),
            nn.Sigmoid(),
            nn.MaxPool2d(2, 2),
            d2l.FlattenLayer(),
            nn.Linear(16*4*4, 120),
            BatchNorm(120, num_dims=2),
            nn.Sigmoid(),
            nn.Linear(120, 84),
            BatchNorm(84, num_dims=2),
            nn.Sigmoid(),
            nn.Linear(84, 10)
        )
print(net)

打印结果为：

5.2 加载数据

##cpu要调小batchsize
batch_size=16

def load_data_fashion_mnist(batch_size, resize=None, root='/home/kesci/input/FashionMNIST2065'):
    """Download the fashion mnist dataset and then load into memory."""
    trans = []
    if resize:
        trans.append(torchvision.transforms.Resize(size=resize))
    trans.append(torchvision.transforms.ToTensor())
    
    transform = torchvision.transforms.Compose(trans)
    mnist_train = torchvision.datasets.FashionMNIST(root=root, train=True, download=True, transform=transform)
    mnist_test = torchvision.datasets.FashionMNIST(root=root, train=False, download=True, transform=transform)

    train_iter = torch.utils.data.DataLoader(mnist_train, batch_size=batch_size, shuffle=True, num_workers=2)
    test_iter = torch.utils.data.DataLoader(mnist_test, batch_size=batch_size, shuffle=False, num_workers=2)

    return train_iter, test_iter
train_iter, test_iter = load_data_fashion_mnist(batch_size)

5.3 训练网络

lr, num_epochs = 0.001, 5
optimizer = torch.optim.Adam(net.parameters(), lr=lr)
d2l.train_ch5(net, train_iter, test_iter, batch_size, optimizer, device, num_epochs)