PyTorch笔记9-Batch Normalization
本系列笔记为莫烦PyTorch视频教程笔记
github源码
reference1: 网易吴恩达 DL 课程
reference2: 知乎关于 BN 讨论
概要
我们知道 normalize input(归一化输入)可以加速神经网络的训练,那我们是否可以 normalize activation function 并 speed up 网络训练呢,这就是 Batch Normalization(BN) 了,直观上,BN 和归一化输入一样有效。在深度网络的训练中,每一层网络的输入都会因为前一层网络参数的变化导致其分布发生改变,这就要求我们必须使用一个很小的学习率和对参数很好的初始化,但是这么做会让训练过程变得慢而且复杂,这种现象称作 “Internal Covariate Shift”。
对于一个神经网络,前面 layer 的 weight 不断变化时,就会带来后面的 weight 不断变化,而 BN 可以弱化隐藏层权重分布变化的程度,即重整了 Z(Z是关于 weight 和 bias 的线性函数),限制了前面 layer 参数更新而影响 Z 数值分布的程度,使这些数值变得更加稳定,削弱了前面 layer 和 后面 layer 之间的耦合程度,使每一层不过多依赖前面的 layer,最终 speed up 整个网络的训练。
下面演示 BN 的作用
import torch
from torch import nn
from torch.nn import init
from torch.autograd import Variable
import torch.utils.data as Data
import torch.nn.functional as F
import matplotlib.pyplot as plt
import numpy as np
torch.manual_seed(1)
np.random.seed(1)
%matplotlib inline生成数据
人工伪造数据,用来模拟真实情况,
# train data size
DATA_SIZE = 2000
# mini batch size, 2^n
BATCH_SIZE = 64
# fake data
# training set
# The newaxis object can be used in all slicing operations to create an axis of length one. newaxis is an alias for ‘None’, and ‘None’ can be used in place of this with the same result.
x = np.linspace(-7, 10, DATA_SIZE)[:, np.newaxis]
y = np.square(x) - 5 + np.random.normal(0, 2, x.shape)
x, y = torch.from_numpy(x).float(), torch.from_numpy(y).float()
# test set
test_x = np.linspace(-7, 10, 200)[:, np.newaxis]
test_y = np.square(test_x) - 5 + np.random.normal(0, 2, test_x.shape)
test_x = Variable(torch.from_numpy(test_x).float(), volatile=True) # not for computing gradients
test_y = Variable(torch.from_numpy(test_y).float(), volatile=True)
# dataset
train_dataset = Data.TensorDataset(data_tensor=x, target_tensor=y)
# dataloader
train_loader = Data.DataLoader(
dataset=train_dataset,
batch_size=BATCH_SIZE,
shuffle=True,
num_workers=2
)
# training set scatter
plt.scatter(x.numpy(), y.numpy(), s=30, label='train')
plt.legend(loc='upper left')
plt.show()搭建神经网络
如何搭建 带有 BN 的神经网络?BN 其实可以看做是一个 layer(BN layer),我们就像平时加层一样价 BN layer 就好了。注意,这里还对输入数据进行了一个 BN 处理(即归一化输入)。
- 注1:下面的 momentum 不是用来更新缩减和平移参数的, 而是用来平滑化 batch mean and stddev 的
# hidden num
N_HIDDEN = 8
# init bad bias parameter for simulation
B_INIT = -0.2
# activation function
ACTIVATION_FUNC = F.relu # or F.tanh
class Net(nn.Module):
def __init__(self, batch_normalization=False):
super(Net, self).__init__()
self.do_bn = batch_normalization
self.fcs = [] # store hidden layer
self.bns = [] # store bn layer
if self.do_bn: self.bn_input = nn.BatchNorm1d(1, momentum=0.5) # BN for input
for i in range(N_HIDDEN):
input_size = 1 if i == 0 else 10 # 1 neuron for input layer, 10 for hidden layers
fc = nn.Linear(input_size, 10)
setattr(self, 'fc%i' % i, fc) # attention!!! fc must set to be class attribute at PyTorch
self._set_init(fc) # init parameters NOT default by PyTorch
self.fcs.append(fc)
if self.do_bn:
bn = nn.BatchNorm1d(10, momentum=0.5) # BN for hidden layer
setattr(self, 'bn%i' % i, bn) # attention!!!
self.bns.append(bn)
self.predict = nn.Linear(10, 1) # output layer
self._set_init(self.predict)
def _set_init(self, layer):
init.normal(layer.weight, mean=0., std=.1)
init.constant(layer.bias, B_INIT)
def forward(self, x):
if self.do_bn: x = self.bn_input(x) # BN for input layer
layer_input = [x]
for i in range(N_HIDDEN):
x = self.fcs[i](x)
if self.do_bn: x = self.bns[i](x) # BN for hidden layer
x = ACTIVATION_FUNC(x)
layer_input.append(x)
out = self.predict(x)
return out, layer_input
# two net, with BN, NOT BN
nets = [Net(batch_normalization=False), Net(batch_normalization=True)]
print(nets)[Net (
(fc0): Linear (1 -> 10)
(fc1): Linear (10 -> 10)
(fc2): Linear (10 -> 10)
(fc3): Linear (10 -> 10)
(fc4): Linear (10 -> 10)
(fc5): Linear (10 -> 10)
(fc6): Linear (10 -> 10)
(fc7): Linear (10 -> 10)
(predict): Linear (10 -> 1)
), Net (
(bn_input): BatchNorm1d(1, eps=1e-05, momentum=0.5, affine=True)
(fc0): Linear (1 -> 10)
(bn0): BatchNorm1d(10, eps=1e-05, momentum=0.5, affine=True)
(fc1): Linear (10 -> 10)
(bn1): BatchNorm1d(10, eps=1e-05, momentum=0.5, affine=True)
(fc2): Linear (10 -> 10)
(bn2): BatchNorm1d(10, eps=1e-05, momentum=0.5, affine=True)
(fc3): Linear (10 -> 10)
(bn3): BatchNorm1d(10, eps=1e-05, momentum=0.5, affine=True)
(fc4): Linear (10 -> 10)
(bn4): BatchNorm1d(10, eps=1e-05, momentum=0.5, affine=True)
(fc5): Linear (10 -> 10)
(bn5): BatchNorm1d(10, eps=1e-05, momentum=0.5, affine=True)
(fc6): Linear (10 -> 10)
(bn6): BatchNorm1d(10, eps=1e-05, momentum=0.5, affine=True)
(fc7): Linear (10 -> 10)
(bn7): BatchNorm1d(10, eps=1e-05, momentum=0.5, affine=True)
(predict): Linear (10 -> 1)
)]
训练
两个神经网络分开训练,为控制单一变量(是否有 BN ),训练的环境(optimizer, lr, loss)都一样
# learning rate
LR = 0.03
# epoch num
EPOCH = 12
optimizers = [torch.optim.Adam(net.parameters(), lr=LR) for net in nets]
loss_func = torch.nn.MSELoss()
# training
for epoch in range(EPOCH):
for step, (batch_x, batch_y) in enumerate(train_loader):
batch_x, batch_y = Variable(batch_x), Variable(batch_y)
for net, opt in zip(nets, optimizers):
predict, _ = net(batch_x)
loss = loss_func(predict, batch_y)
opt.zero_grad()
loss.backward()
opt.step()测试并出图
# set net to eval mode to freeze the parameters in batch normalization layers
[net.eval() for net in nets] # set eval mode to fix moving_mean and moving_var
predictions = [net(test_x)[0] for net in nets]
plt.figure(3)
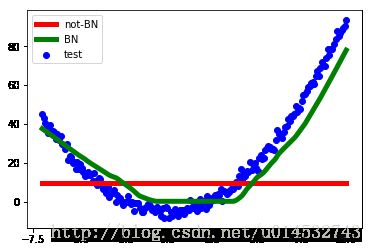
plt.scatter(test_x.data.numpy(), test_y.data.numpy(), c='b', label='test')
plt.plot(test_x.data.numpy(), predictions[0].data.numpy(), lw='5', c='r', label='not-BN')
plt.plot(test_x.data.numpy(), predictions[1].data.numpy(), lw='5', c='g', label='BN')
# plt.ylim((0, 2000))
plt.legend(loc='best')
plt.show()上面是使用 relu 作为激励函数的结果, 我们可以看到, 没有使用 BN 的误差要高, 线条(红色线条)不能拟合数据, 原因是我们有一个 “Bad initialization”, 初始 bias = -0.2, 这一招, 让 relu 无法捕捉到在负数区间的输入值. 而有了 BN(绿色线条), 这就不成问题了