【深度学习与无线通信：论文阅读】：Power of Deep Learning for Channel Estimation and Signal Detection in OFDM Systems

前言

论文题目： Power of Deep Learning for Channel Estimation and Signal Detection in OFDM Systems
论文地址： https://ieeexplore.ieee.org/document/8052521/
github源码地址: https://github.com/haoyye/OFDM_DNN
利用keras的简化代码: https://github.com/TianLin0509/DNN_detection_via_keras

这篇文章是无线通信与深度学习的经典之作， 作者找到了一个非常好的切入点， 很合理地将深度学习的成熟技术应用到了通信物理层的处理之中， 目前也应该是同领域的引用之首， 也成为许多同学争相学习的文章。 这里根据我自己的认识写一篇中文的解析， 希望可以帮助大家更好地理解。

中心思想

因为是18年的文章， 文章用了大量篇幅介绍了基础的深度学习知识。 这一部分笔者就跳过了，和中心思想无关 （并非说文章不好，相反，我觉得作者的介绍极为精炼）。本文的实质核心是Secion II 的 B部分：

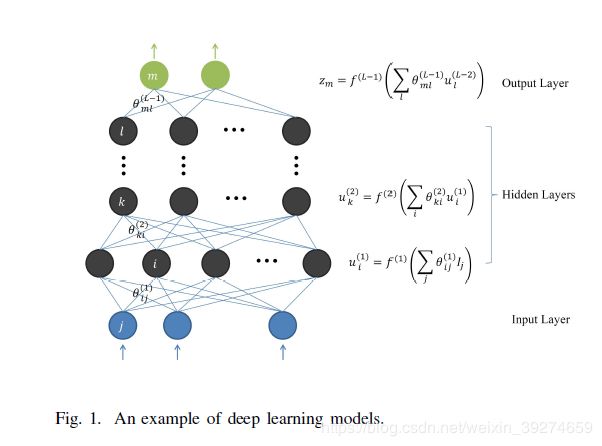
大家首先注意到本文的题目： Power of Deep Learning for Channel Estimation and Signal Detectionin OFDM Systems。 顾名思义， 本文作者的中心思想就是： 用神经网络来代替传统通信中的信道估计和信号检测部分。 需要注意的是， 作者不是使用两个独立的神经网络，分别完成信道估计和信号检测， 而是直接用一个神经网络来同时完成这两部分的工作。 这一点非常有意义， 传统的通信受限于设计的复杂度， 在过去几十年的积淀中， 整个通信接收的处理过程被有条不紊地分隔成 同步， 校正频偏， 信道估计， 信号检测等多个各司其职的独立模块，每个模块都有学者进行了独立的研究。 然而， 神经网络在计算机视觉和自然语言处理等领域的杰出表现， 证明了其可以拟合各种复杂函数的强大能力。 那这样就很自然的让人想到， 既然神经网络这么强大， 我们还需要把信号接收拆分成那么多模块吗？ 直接一个网络搞定所有 （事实上无线通信已经有许多end-to-end的神经网络相关工作）！我举个例子： 传统的验证码识别中， 算法往往包括了 去噪， 分隔， 识别等多个步骤， 非常繁琐。 而基于深度学习的验证码识别算法则一步到位——把验证码图片输入神经网络， 直接输出识别出的验证码数字。 言归正传， 这篇文章也证明了， 一个神经网络，就可以完美地替代 传统通信中的 信号估计和信号检测 部分。

具体实现

说了作者的核心思想， 那么具体是怎么实现的呢？ 在讲这个之前， 我们首先要知道， 传统通信是怎么做的， 并从中得到启发。

用最简单的例子来讲解一下：

假设基站发送的信号为x， 信道为 h, 不考虑噪声的话， 那么接收信号 y = hx。 而接收端要做的就是从y恢复出原始信号x。 显然，这非常容易， x = y / h， 小学数学题。 这里的问题在于，接收端并不知道h是什么~因此， 就需要信道估计， 来估计出h。 思路也非常简单， 基站会先发送一个pilot信号x1 (实际中为了估计的更准确， 往往是发送一串），这个pilot信号，中文被称为导频信号。 这个是基站和接收端约定好的，也就是说，接收端是已知x1的。 这时候， 接收端接收到的经过信道的信号就是 y = hx1， 那么就可以再用小学数学解出 h = y / x1。这就是信道估计的思路。 当然在实际中由于噪声等问题， 不会这么简单地处理， 比如会用MSE准则来估计等。 但万变不离其宗， 传统通信的基本思想就是这样。

这就可以启发 神经网络 的设计和实现。 我们现在知道，作者的目标是用神经网络替代信道估计和信号检测。 而神经网络的设计， 其实本质上就是设计三个东西：

• 输入是什么， 输出又是什么
• 损失函数是什么
• 网络具体的架构

我们先讲后两个——损失函数， 其实浑然天成。 既然神经网络要做的是信号检测， 那么我们期望的是神经网络的输出结果就是原始发送信号x， 也就是说， 标签就是原始发送信号x。 在物理层通信中， x就是0或1。 那么这就是深度学习中基础的二分类问题——可以用交叉熵或mse作为损失函数。 本文中， 作者选用了mse作为损失函数, 即：

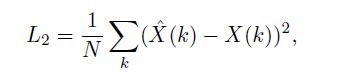
网络的具体架构， 这个在CV或NLP领域也许比较重要，但这在无线通信中，其实并不关键。 因为无线通信中往往不需要很复杂的神经网络架构， 那么，DNN全连接网络（Dense网络）往往是最好的网络选择——CNN或RNN都可以看做DNN的特例。在没有面临训练难度的时候， 全连接网络是最好的万金油。 本文的神经网络就是由5层全连接层组成，分别用了256, 500， 250， 120， 16个神经元。 这个数量级是无论如何也算不上大网络的，因此网络的架构其实并不是本文的重点。 更合理地应该说， 作者找到了一个很好的神经网络的应用场景，然后随便找了一个基本的网络，就得到了很好的效果。

最重要的就是， 输入和输出分别是什么？ 输出，很容易理解， 既然我们的目的是要恢复出原始信号， 那我们的输出值就是我们恢复的信号呗。 （但这里需要一些处理， 后面再详细说） 那么输入是什么呢？ 显然，我们应该把可用的信息都给到神经网络， 那在这个例子中， 可用的信息就是接收到的数据y， 这就是网络的输入。 但是刚刚不是说到嘛，传统中是需要通过信道估计来获取h的信息， 才能从y回复出x。那对于我们这个神经网络，难道也要先用传统的信道估计估计出h，再把h和y一起输入神经网络嘛？ 不！这样太傻啦！

正确的打开方式是：

基站发送导频信号后用户得到的接收信号记为y1， 基站发送的数据信号，用户得到的接收信号记为y2， 我们直接把[y1, y2]一起输入神经网络， 那么神经网络就一定有能力恢复出原始信号！
原因？ 很简单， 我们把传统方法中所用到的所有信息都给了网络， 传统算法都能做到的东西， 难道神经网络做不好吗？ 这可是能战胜李世石的东西！

因此， 神经网络的输入就是导频的接收信号和数据接收信号。

实现细节

上一节中， 用最简单的语言讲述了本文的核心架构。 这一节讲实现的细节：

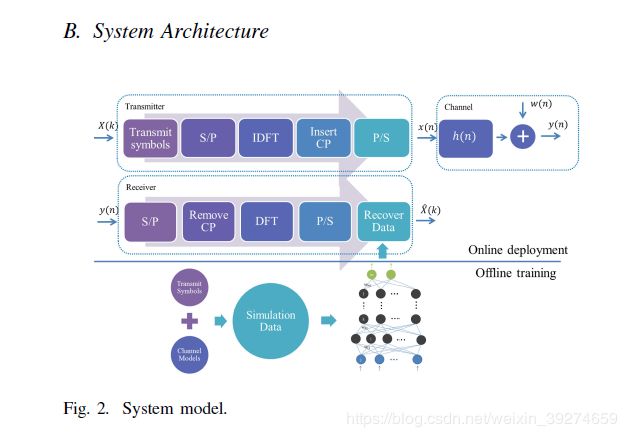
• OFDM系统： 本文是基于OFDM架构， 这里就不详细解释了，大家可以自行百度。 简单地说下就是， 我刚刚举的例子， x都是一个一个比特的发送， 在实际的OFDM系统中， 信号是一帧一帧的发送， 比如64个比特组成一帧，再通过FFT， IFFT等操作到频域端处理~这里大家只要记住， y = hx中， x 和 y 都是向量（含有多个比特）。 举文中的一个例子： 基站先发送了一帧64 * 1的导频信号， 再发送了一帧64 * 1的数据信号， 那么接收端总共收到的就是128*1的一个向量。 注意， 通信中因为信号分为I路和Q路发送， 所以向量中的每个元素都是一个复数。 而主流的深度学习框架（tensorflow， pytorch）往往都是只支持实数操作的，所以文中采用的操作就是把向量的实部和虚部拆分后再拼接成一个256 *1的实数向量， 即向量的前128个元素是原向量的实部， 后128个元素是虚部。 从信息的角度看， 原复数向量的信息没有任何丢失地输入到了网络中。
• 导频数据， 以上个例子为例。 作者令基站发送两帧信号，第一帧为导频，第二帧为数据。 那么需要注意的重点是——这个导频序列可以是任意的 （ 1 0 0 1 … 或是 0 0 1 1…并不重要）， 但必须是统一的。 即训练和测试中的导频序列要永远保持一致。 这一点很容易理解——用同一个导频序列， 对网络进行训练，那么在训练的过程中， 网络会逐渐地学习到这个导频序列， 并会以这个导频序列来进行信号处理。 结果你在测试的时候，突然换了另一个导频序列， 那显然网络就工作不了了， 坑网络也不是这么坑的哈~
• 多个网络并行。 这一点很多读者都容易想不通， 但其实非常简单。 还是刚刚的例子， 基站发送了两帧数据， 其中第二帧的64 * 1的复数向量是数据， 即128个比特的信息。 那么最直接的就是指定网络的输出就是128 * 1的实数向量， 每个元素对应每个恢复的比特。 但是作者没有采用直接的思路， 文章的做法是使用8个并行的网络， 每个网络的输入和结构都一模一样， 分别负责16个比特的检测。 加起来就检测了所有128个比特。比如第一个网络检测的是1-16个比特， 第二个就是17-32个比特…。 这里主要有两个注意点： 1. 每个网络虽然只检测16个比特， 但是都会输入所有的接收信号。 这是因为OFDM系统中每个比特都和所有的接收信号相关。 即使不从通信的角度考虑， 我们也应该把所有可得的信息都交给网络来处理。 2. 其实是可以只用一个网络来直接检测128个比特， 但根据笔者的实践，一个网络的性能即误码率，性能比分成8个网络差了不少。 因此，虽然分成8个网络增加了复杂度， 但是性能上提升了很多。 这里提一句： 在代码中， 其实只需要仿真一个网络就可以了， 而不需要仿真8个网络——因为我们的目标是误码率，这本来就是比特的平均值，所以1个网络的误码率和8个网络是一样的， 因此仿真一个网络的结果和8个网络的结果一样，能明白吗？

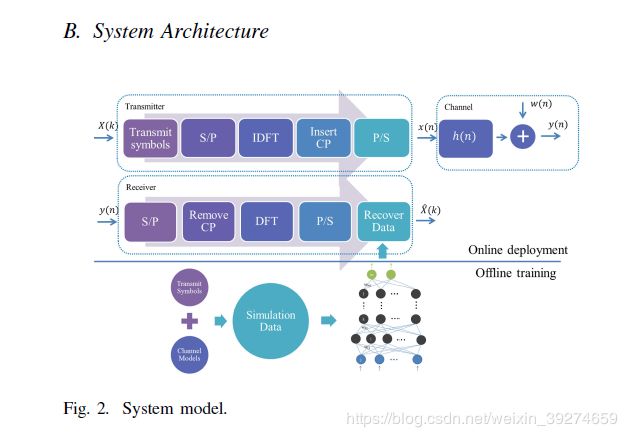
再说一下整体的流程。 还是这张图，在线下训练过程中， 先使用仿真， 得到了一堆训练数据。 什么是训练数据呢？ 其实就是仿真产生了不同的信道 和 发送数据（包括不变的导频和变化的数据x）， 然后把发送数据通过信道再加上噪声， 得到了接收信号y。 这个接收信号y就是输入信号， 数据x就是标签。 {x,y}就可以看成一个样本。 在线下训练时，我们生成100万个样本（这个100万只是我随口说的，相信堵读者们不会这么死板哈）对网络进行训练。 随着训练的迭代， 损失函数越来越小， 也就是说，网络恢复出的数据和原始数据越来越接近。 训练完毕时，我们将网络中的参数权重都固定， 不再改变。 在线上使用时，只需将接收信号通过网络， 就可以获得恢复信号了。 注意： 这时网络的权重已经固定， 因此复杂度仅仅只是做了几个矩阵相乘运算而已， 非常低（真正耗时的网络训练部分在线下可以提前完成， 比如你可以在使用前先花个一天训练好模型，而真正使用的时候是不需要对网络进行训练的）。

仿真结果

最后，来看一下网络的性能。

作者再做仿真的时候，可以认为分为了两种情况——理想情况与非理想情况。 比如下图：

64Pilots就是比较理想的情况——充足的导频信号，可以做好信道估计。 可以看到， 神经网络的性能在这时候是和传统方法差不多的。 其实应该说是略逊——这其实可以认为传统方法差不多做到了这种通信框架下的极限性能， 神经网络也难以更进一步。 笔者尝试过调整用更复杂的网络， 但性能也难以突破。 那是否说明神经网络就没什么意义了呢？ 其实不然， 作者从鲁棒性角度， 阐释了网络相比于传统算法更好的适应能力。

图中同时展示了8个Pilots的场景， 这代表了匮乏的导频信号——传统方法的信道估计几乎无法实施，因此可以看到， 无论是LS还是MSE方法， 性能都巨差无比，可以说是不能工作了。 而神经网络的方法虽然相比于64Pilots有所下滑， 但相比于传统算法有巨大的增益。

这个仿真结果不仅体现了神经网络的鲁棒性， 也有很重要的实际意义——我们其实可以减少导频信号的数量。 这其实是变向提升了传输的速率， 节约的导频信号就可以用来传输数据了。

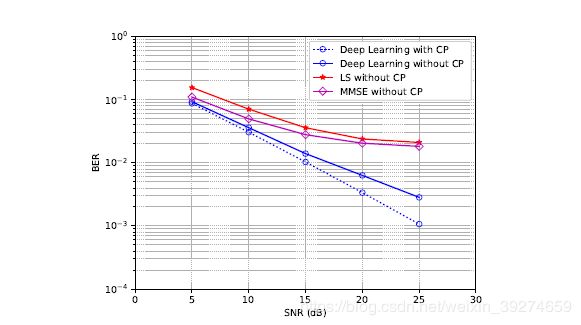
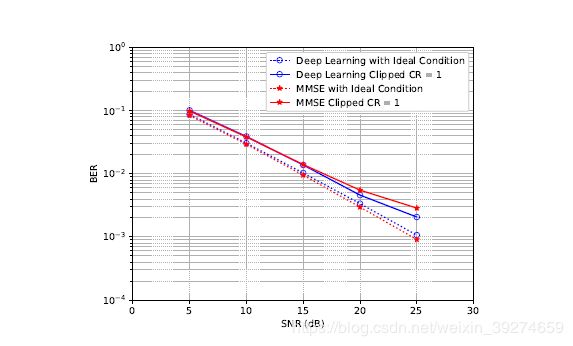
作者后续又做了其他非理想情况的仿真，比如没有CP的场景等等，也算是一种探索。仿真结果也大同小异，在非理想场景下， 神经网络展现了远胜于传统算法的性能。

总结

这篇文章作为深度学习和无线通信结合的经典之作， 我认为有标杆的意义：

• 精彩地演绎了如何找到一个好的切入点，把深度学习引入到通信系统中
• 用一个神经网络来代替传统通信中多个模块的工作，未来也许可以实现大一统
• 神经网络在非理想情况下具有更强的鲁棒性