统计学习方法——逻辑斯蒂回归与最大熵模型（一）

逻辑斯蒂回归与最大熵模型

逻辑斯蒂回归是统计学中常用的经典分类方法；
最大熵是概率模型学习的一个准则，扩展到分类问题得到最大熵模型。
都属于对数线性模型

逻辑斯蒂回归模型

逻辑斯蒂分布

设$X$为连续随机变量，$X$服从逻辑斯蒂分布是指$X$具有如下的分布函数和密度函数：
$$F\left(x\right)=P\left(X\le x\right)=\frac{1}{1+e^{-\left(x-\mu \right)/\gamma }}$$
$$f\left(x\right)=F^{\prime }\left(x\right)=\frac{e^{-\left(x-\mu \right)/\gamma }}{\gamma {\left(1+e^{-\left(x-\mu \right)/\gamma }\right)}^2}$$
其中$\mu$为位置参数，$\gamma >0$为形状参数。

其图像如下所示：

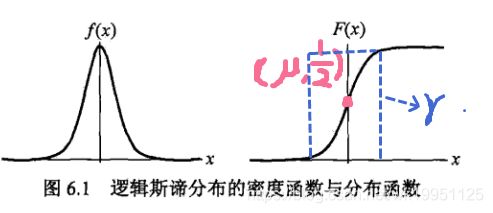
可以发现图形为$S$形曲线，以点$\left(\mu ,\frac{1}{2}\right)$中心对称，$\gamma$越小，曲线在中心附近增长越快。

二项逻辑斯蒂回归模型

• 逻辑斯蒂回归模型
  二项式逻辑斯蒂回归模型的条件概率如下：
  $$P\left(Y=1|x\right)=\frac{\exp \left(w\cdot x+b\right)}{1+\exp \left(w\cdot x+b\right)}$$
  $$P\left(Y=0|x\right)=\frac{1}{1+\exp \left(w\cdot x+b\right)}$$
  这里$x$为输入，$Y\in \left\{0,1\right\}$为输出，$w$和$b$为参数，$w\cdot x$为内积。
• 特点
  • 输出$Y=1$的对数几率是输入$x$的线性函数
    设事件发生的概率为$p$，则发生几率为$\frac{p}{1-p}$，对数几率为：
    $$logit\left(p\right)=\log \frac{p}{1-p}=\log \frac{P\left(Y=1|x\right)}{1-P\left(Y=1|x\right)}=w\cdot x+b$$

模型参数估计

对于逻辑斯蒂回归模型学习时，可以使用最大似然估计算法估计模型参数。

---

训练集为$T=\left\{\left(x_1,y_1\right),\cdots ,\left(x_N,y_N\right)\right\}$，$x_i\in R^n$，$y_i\in \left\{0,1\right\}$。
设$P\left(Y=1|x\right)=\pi \left(x\right)$，$P\left(Y=0|x\right)=1-\pi \left(x\right)$，则似然函数为：
$$\prod _{i=1}^N{\left[\pi \left(x_i\right)\right]}^{y_i}{\left[1-\pi \left(x_i\right)\right]}^{1-y_i}$$
对应的对数似然函数为：
$$L\left(w\right)=\sum _{i=1}^N\left[y_i\log \pi \left(x_i\right)+\left(1-y_i\right)\log \left(1-\pi \left(x_i\right)\right)\right]=\sum _{i=1}^N\left[y_i\left(w\cdot x_i\right)-\log \left(1+\exp \left(w\cdot x_i\right)\right)\right]$$
求取$L\left(w\right)$的极大值就可以得到$w$的估计值。

---

多项逻辑斯蒂回归

假设离散型随机变量$Y$的取值集合为$\left\{1,2,\cdots ,K\right\}$，则多项逻辑斯蒂回归模型为：
$$P\left(Y=k|x\right)=\frac{\exp \left(w_k\cdot x\right)}{1+\sum _{i=1}^{K-1}\exp \left(w_i\cdot x\right)}k=1,2,\cdots ,K-1$$
$$P\left(Y=K|x\right)=\frac{1}{1+\sum _{i=1}^{K-1}\exp \left(w_i\cdot x\right)}$$
二项逻辑斯蒂回归的参数估计可以类似推至多项逻辑斯蒂回归。

最大熵模型

最大熵原理

• 最大熵原理：学习概率模型时，在所有可能的概率模型（分布）中，熵最大的模型是最好的模型。
• 解释来说：选择的模型首先要满足已有事实（约束条件），剩下不确定的部分都是“等可能的”，最大熵原理则是通过熵的最大化来表示等可能性。

最大熵模型的定义

• 学习目标：用最大熵原理选择最好的分类模型。
• 最大熵模型
  假设满足所有约束条件的模型集合为
  $$\mathcal{C}=\left\{P\in \mathcal{P}|E_p\left(f_i\right)=E_{\tilde{p}}\left(f_i\right),i=1,2,\cdots ,n\right\}$$
  其中$E_{\tilde{P}}\left(f\right)=\sum _{x,y}\tilde{P}\left(x,y\right)f\left(x,y\right)$，$E_P\left(f\right)=\sum _{x,y}\tilde{P}\left(x\right)P\left(y|x\right)f\left(x,y\right)$，$f\left(x,y\right)=\{\begin{array}{l}1x与y满足某一事实\\ 0不满足\end{array}$。定义在条件概率分布$P\left(y|x\right)$上的条件熵为：
  $$H\left(P\right)=-\sum _{x,y}\tilde{P}\left(x\right)P\left(y|x\right)\log P\left(y|x\right)$$
  则模型集合$\mathcal{C}$中条件熵$H\left(P\right)$最大的模型称为最大熵模型。

最大熵模型的学习

• 最大熵学习可以形式化为约束最优化问题。
  对于给定的训练集$T=\left\{\left(x_1,y_1\right),\cdots ,\left(x_N,y_N\right)\right\}$以及特征函数$f_i\left(x,y\right),i=1,2,\cdots ,n$，最大熵模型的学习等价于约束最优化问题：
  $$\underset{P\in \mathcal{C}}{\max }H\left(P\right)=-\sum _{x,y}\tilde{P}\left(x\right)P\left(y|x\right)\log P\left(y|x\right)$$
  $$s.t.E_P\left(f_i\right)=E_{\tilde{P}}\left(f_i\right),i=1,2,\cdots ,n$$
  $$\sum _{y}P\left(y|x\right)=1$$

极大似然估计

• 最大熵模型的学习问题可以转化为求解对数似然函数极大化或对偶函数极大化的问题。
• 最大熵模型的一般形式
  $$P_w\left(y|x\right)=\frac{1}{Z_w\left(x\right)}\exp \left(\sum _{i=1}^n{w}_i{f}_i\left(x,y\right)\right)$$
  其中$$Z_w\left(x\right)=\sum _y\exp \left(\sum _{i=1}^n{w}_i{f}_i\left(x,y\right)\right)$$
  $x\in R^n$为输入，$y\in \left\{1,2,\cdots ,K\right\}$为输出，$w\in R^n$为权值向量，$f_i\left(x,y\right),i=1,2,\cdots ,n$为任意实值特征函数。

参考文献

《统计学习方法》