【深度学习论文阅读】TCN:An Empirical Evaluation of Generic Convolutional and Recurrent Networks for Sequence
2018年人工智能十佳论文之一:TCN
论文地址:An Empirical Evaluation of Generic Convolutional and Recurrent Networks for Sequence Modeling
项目地址:TCN的github链接
文章目录
- 1. ABSTRACT
- 2. INTRODUCTION & BACKGROUND
- 2.1 Temporal Convolutional Networks
- 2.2 Sequence Modeling (序列建模)
- 2.2.1 整体构架:
- 2.3 Casual Convolutions(因果卷积)
- 2.4 Dilated Convolutions(膨胀卷积、空洞卷积)
- Residual Connections
- 2.5 Discussion
- 3. Sequence Modeling Tasks & Experiments(序列模型任务 & 实验)
- 4. Conclusion
- 膨胀卷积

1. ABSTRACT
对于大多数 深度学习研究者而言,序列建模任务等价于RNN。但是最近的研究表明,在音频合成以及机器翻译等任务上,CNN的表现胜过RNN。对于新的序列建模任务,RNN还是CNN,该如何选择? 作者通过对用于RNN性能的标准任务来评估CNN的性能。结果证实,简单的CNN结构在不同的任务以及数据集上的性能优于LSTM这类典型的RNN模型。作者认为,应该重新考虑序列任务与RNN、CNN之间的联系,甚至是将CNN作为序列建模任务的起点。(作者在文中将其记做TCN)
2. INTRODUCTION & BACKGROUND
近期的研究者发现,在音频合成、单词级语言建模以及机器翻译等任务上的性能精度高于传统认为的最优解决方案的LSTM以及GRU,作者思考CNN在序列建模上的成功是针对特定领域呢,还是它在所有序列建模任务上表现都很好?
作者设计一系列序列建模任务来评估,包含复调音乐建模、单词级和字符级语言建模任务以及压力测试任务等。结果表明。CNN架构它在音频处理领域的成功并不局限于这些领域。
除此之外,尽管循环神经网络具有长期记忆的能力,但是CNN架构(文中的TCN)表现出更加长期的记忆能力。
背景部分主要是讲 序列建模领域的研究进展,包括对RNN的改进,对LSTM的改进等等,到后来对LSTM加入卷积操作等等,这里不详谈。
2.1 Temporal Convolutional Networks
我们首先描述卷积序列预测的一般架构。我们的目标是将卷积网络设计中的最佳实践提炼为一个简单的架构,它可以作为一个方便而强大的起点。我们将提出的体系结构称为时间卷积网络(TCN),并强调我们采用这个术语并不是作为一个真正的新体系结构的标签,而是作为一个简单的描述一系列体系结构的术语。TCNs的显著特点是:1)结构上的卷积是因果关系,即没有从未来到过去的信息泄漏;2)体系结构可以获取任意长度的序列,并将其映射到相同长度的输出序列,就像使用RNN一样。除此之外,我们强调如何构建非常长的有效历史规模(即通过结合非常深的网络(用剩余层增强)和膨胀的卷积,网络能够看到非常遥远的过去并做出预测
我们的体系结构借鉴了最近的卷积序列数据体系结构(van den Oord et al., 2016;Kalchbrenner等,2016;Dauphin等,2017;Gehring等人,2017a;例如,TCN比wavenet (van den Oord et al., 2016)简单得多(没有跨层的跳过连接、条件设置、上下文叠加或门控激活)。
与Dauphin等人(2017)的语言建模体系结构相比,TCNs不使用门控机制,内存更长。
2.2 Sequence Modeling (序列建模)
对于某一个输入序列{ X 0 , X 1 , X 3 , . . . , X t − 1 , X t , X t + 1 , X t + 2 {X_0,X_1,X_3,...,X_{t-1},X_t,X_{t+1},X_{t+2}} X0,X1,X3,...,Xt−1,Xt,Xt+1,Xt+2},希望预测一些相应的输出{ Y 0 , Y 1 , Y 2 , . . . , Y t − 1 , Y t , Y t + 1 , Y t + 2 Y_0,Y_1,Y_2,...,Y_{t-1},Y_t,Y_{t+1},Y_{t+2} Y0,Y1,Y2,...,Yt−1,Yt,Yt+1,Yt+2}。如果我们将这样一个问题试做序列问题,其中最关键的一点是,假如要预测 t t t时刻的输出,那么我们只能使用 t t t时刻之前的记录作为输入,如{ X 0 , X 1 , X 3 , . . . , X t − 1 , X t {X_0,X_1,X_3,...,X_{t-1},X_t} X0,X1,X3,...,Xt−1,Xt},也就是找到一个从输入到输出的映射,表示如下:

对于每个时刻的输出,都计算与真实值之间的差异,并且尽可能的减少这个差异,也即最小化这个损失函数:
![]()
上述的模型类似于自回归预测,但是不同于机器翻译等问题,因为在机器翻译、机器推理等问题中,均以所有时刻的取值作为输入。
2.2.1 整体构架:
- 网络的上一层到下一层,输入与输出的长度相同
- 不存在利用将来信息的情形
文中的做法是:
- 针对第一点使用Full-Convolutional ,全卷积神经网络FCN架构。
- 使用casual convolution
2.3 Casual Convolutions(因果卷积)
因果卷积只是个叫法,保证t时刻的输出只与前一层t时刻以及更早的元素进行卷积。(我感觉就是传统的卷积操作)
回顾一下以前模型中VGG里面说2个3 * 3的filter等价于一个5 * 5的filter、3个3 * 3的filter等价于一个7*7的filter。假如这3个filter相邻,最后得到的感受野大小即是7 * 7,计算公式是:receptive field = (filter_size -1) * num+1 = (3-1)*3+1
但这种做法存在的问题是,如果整个网络需要记录非常多的信息,那么势必会导致网络模型的深度急剧增加。为此作者的做法是使用Dilated Convolution。
2.4 Dilated Convolutions(膨胀卷积、空洞卷积)
一个简单的因果卷积只能用网络深度的线性大小来回顾历史。这使得将上述因果卷积应用于序列任务非常困难,特别是对于需要长期记忆的问题,如机器翻译、逻辑推理等。
作者的做法是采用dilated convolution,又称膨胀卷积、空洞卷积,下称膨胀卷积,能够以指数形式增加感受野,对于一维的输入序列 X X X、卷积核 f : f: f:{ 0 , 1 , 2 , . . . , k − 1 {0,1,2,...,k-1} 0,1,2,...,k−1},膨胀卷积操作可表示为:

其中d是膨胀系数,k是卷积核大小, X s − d ⋅ i X_{s-d·i} Xs−d⋅i代表过去的数据。
看公式看不太明白,在文末解释dilated convlution
Residual Connections
ResNet中的快速通道使得模型学习差异信息,这一点在深层网络中十分有效且十分必要。p
这有效地允许层学习对标识映射的修改,而不是整个转换,这已多次被证明有利于非常深入的网络。对于本文中的TCN模型,如果想要使模型记录非常多的历史信息,就要求模型最后的感受野足够的大,感受野大小又依赖于网络深度、滤波器大小以及扩张系数。例如预测可能依赖于 2 12 2^{12} 212的历史记录以及高纬度的输入序列,那么则需要多大12层的网络,所以TCN采用了ResNet构架。

其中包含每一个Residual block模块包含两层Dilated conv,ReLU,BN操作采用weight normalization,此外在激活函数之后还使用spatial dropout。
而对于ResNet中可能存在的输入输出的长度不一致时,增加了1*1 conv以确保元素内积得到同样大小的tensor。
2.5 Discussion
TCN包含以下优点:
- 并行 RNN模型某一时刻的计算需依赖于上一层的计算结束,但是由于卷积核一致,CNN中卷积操作可以并行计算。因此,无论是在训练还是评估中,TCN都能够保存更加长期的记忆。
- 感受野的大小灵活 TCN可以通过叠加更多的扩张卷积层、使用更大的扩张因子或者使用更大的卷积核来增加感受野,所以TCN能够更加灵活的空值模型的内存大小,并且容易迁移到其它领域中。
- 梯度稳定 TCN具有不同于序列时间方向的反向传播路径,避免了RNN中的梯度爆炸和梯度消失问题。
- 训练时内存需求低 输入序列非常长的情况下,LSTM和GRU需要使用大量的内存来存储门结构的结果。而TCN中卷积核是跨层贡献的,反向传播的路径仅仅依赖于网络的深度。
- 可变长度的输入 与RNN一样,TCN也可以通过滑动一维卷积核来接收任意长度的输入
同样的TCN也有以下两个缺点:
- 评估期间的数据存储 在评估/测试中,为了生成预测,RNNs只需要保持一个隐藏状态并接受一个当前输入 x t x_t xt。也即整个历史的总结是由固定长度的 h t h_t ht向量表示,实际观测到的序列可以被丢弃。相比之下,TCN需要将原始序列保留到有效历史长度,因此在评估时可能需要更多的内存
- 领域转化时潜在的参数变化。为了进行预测,不同的领域可能对模型所需的历史记忆有不同的需求。所以,当其记忆长度由短变长时,TCN可能表现不好,因为没有足够大的感知域。
3. Sequence Modeling Tasks & Experiments(序列模型任务 & 实验)
包含如下模型序列任务:
- adding problem. 加法问题,每个输入由一个深度为2的序列组成,所有值从[0,1]中随机选取。在第二维度中,除第一维被标记为1的元素外,其余数均为0。将两个随机值相加,如果为1,则其MSE为0.1767。被用于序列模型的压力测试。
- Sequential MNIST and P-MNIST. Sequential MNIST用来测试一个循环网络保留遥远过去信息的能力
- Copy memory. 每个输入序列的长度为 T + 20 T+20 T+20,前十个是是从{ 1 , 2 , . . . , 8 1,2,...,8 1,2,...,8}中随机选取的,除最后11个被置为9外,全部为0。目的是生成一个长度相同的输出。除分隔符之后的10个值外,其余数值全部是0.
这里感觉写了没什么太大意思,不写了。 - JSB Chorales and Nottingham
- PennTreebank
- Wikitext-103
- LAMBADA
- text8
实验中所使用的扩张系数为 d = 2 i d=2^i d=2i,其中 i i i是第 i i i层。模型中使用Adam optimizer并且设置learning rate=0.002
4. Conclusion
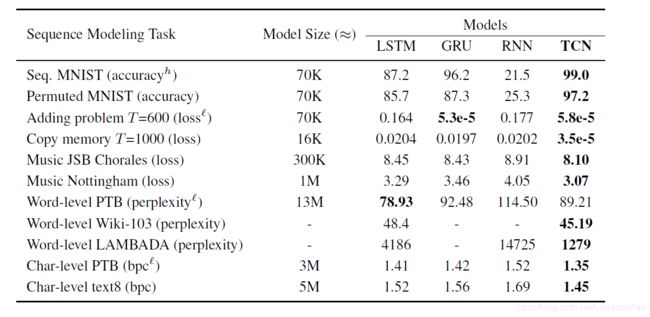
实验结果表明,TCN模型的性能明显优于LSTMs和GRUs等一般的递归体系结构。并且针对于卷积神经网络与循环神经网络的长期记忆能力,在实际应用中,RNN的无限记忆的优势并不存在。与之相比,相同大小的TCN模型表现出更加出色的长期记忆。
膨胀卷积
传统的卷积操作存在一些缺点,较为著名的是 up-sampling 和 pooling layer 。
主要包含:
- Up-sampling / pooling layer (e.g. bilinear interpolation) is deterministic. (参数不可学习)
- 内部数据结构丢失;空间层级化信息丢失。
- 小物体信息无法重建 (假设有四个pooling layer 则 任何小于 2^4 = 16 pixel 的物体信息将理论上无法重建。)
在这样问题的存在下,语义分割问题一直处在瓶颈期无法再明显提高精度, 而 dilated convolution 的设计就良好的避免了这些问题。
想了想,这里还是另起一篇文章系统讲述卷积、反卷积、空洞卷积。
