排序是生活中常常会遇到的问题,也是面试中经常会问的算法,本文简单记录了常见的排序算法,使用C++与Python分别实现。
稳定性
将设ki = kj ( 1 <= i < j <=n ),在序列中的位置ri 领先于 rj,如果排序后 ri依旧领先于 rj,则成为算法是稳定的,反之,如果可能使得排序后的序列中 rj 领先于ri,则称排序为不稳定的。
代码用到公用函数
c++
//utils.h
#include
#include
#include
#include
typedef std::vector IntArray;
typedef IntArray::iterator ArrayIter;
void GetRandomArray(IntArray &array, int min, int max, uint32_t size);
int GetRandom(int min, int max);
void PrintArray(const IntArray &array);
void swap(ArrayIter val1, ArrayIter val2);
void swap(int &a, int &b);
//utils.cc
#include "utils.h"
int GetRandom(int min, int max)
{
srand(clock());
int interval = max - min;
int random = rand() % interval;
return random + min;
}
void GetRandomArray(IntArray &array, int min, int max, uint32_t size){
while(size--){
array.push_back(GetRandom(min, max));
}
}
void PrintArray(const IntArray &array)
{
const int ROW_NUM = 20;
const int WIDTH = 8;
int row_index = 0;
for (IntArray::const_iterator iter = array.begin(); iter != array.end(); iter++)
{
std::cout.setf(std::ios::left);
std::cout.width(WIDTH);
std::cout << *iter;
row_index ++;
if(row_index == ROW_NUM){
std::cout << std::endl;
row_index = 0;
}
}
std::cout << std::endl;
}
void swap(ArrayIter val1, ArrayIter val2){
int temp = *val1;
*val1 = *val2;
*val2 = temp;
}
void swap(int &a, int &b)
{
int temp = a;
a = b;
b = temp;
}
python
import random
CONST_ROW_NUM = 10
def get_random(min, max, num):
return [int(random.random()*(max-min) + min) for i in range(num)]
def print_nums(nums):
for i in range(len(nums)):
if i!=0 and i%CONST_ROW_NUM == 0:
print()
print("%-10d"%(nums[i]), end="")
print()
冒泡排序
两两比较相邻记录,若反序则交换,直到没有反序的记录为止。
从图中可以看到,每一轮比较可以得到待比较序列的最大值,每次将最大值往上移动后,对剩下的序列进行冒泡排序,最终可以得到有序序列。
c++
#include
#include "utils.h"
using namespace std;
void BubbleSort(IntArray &data)
{
bool sort_flag = true;
for (ArrayIter out_iter = data.begin(); out_iter != data.end() && sort_flag; out_iter++)
{
sort_flag = false;
for (ArrayIter in_iter = data.end() - 1; in_iter > out_iter; in_iter--)
{
if(*in_iter < *(in_iter - 1)){
sort_flag = true; //优化,如果没有走到这一步,那么序列现在已经有序,无需在进行下去
int temp = *in_iter;
*in_iter = *(in_iter - 1);
*(in_iter - 1) = temp;
}
}
}
}
int main(int argc, char const *argv[])
{
IntArray data;
GetRandomArray(data, 0, 100, 10);
cout << "Raw input:" << endl;;
PrintArray(data);
BubbleSort(data);
cout << "Result output:"< python
import utils
def bubble_sort(nums):
sort_flag = True
for i in range(len(nums) - 1):
sort_flag = False
for j in range(len(nums)-1, i, -1):
if nums[j] < nums[j-1]:
sort_flag = True
nums[j],nums[j-1] = nums[j-1],nums[j]
if not sort_flag:
break
def main():
nums = utils.get_random(0,100,10)
print("Raw input:")
utils.print_nums(nums)
bubble_sort(nums)
print("Result output:")
utils.print_nums(nums)
if __name__ == "__main__":
main()
时间复杂度
最坏情况下,即序列是逆序的,需要进行1+2+3+...+n=n(n-1)/2次比较,并做同等数量的移动,因此,总的时间复杂度为o(n^2)。
选择排序
通过
n-i次的比较,从n-i+1序列中选择最小(最大)的元素,并和第i个记录进行交换。
c++
#include
#include "utils.h"
using namespace std;
void SelectSort(IntArray &data)
{
for (ArrayIter out_iter = data.begin(); out_iter != data.end(); out_iter++)
{
ArrayIter min_iter = out_iter;
for (ArrayIter in_iter = out_iter + 1; in_iter != data.end(); in_iter++)
{
if (*min_iter > *(in_iter))
{
min_iter = in_iter;
}
}
if (min_iter != out_iter)
{
swap(min_iter, out_iter);
}
}
}
int main(int argc, char const *argv[])
{
IntArray data;
GetRandomArray(data, 0, 100, 10);
cout << "Raw input:" << endl;
PrintArray(data);
SelectSort(data);
cout << "Result output:" << endl;
PrintArray(data);
return 0;
}
python
import utils
def select_sort(nums):
for i in range(len(nums) - 1):
min_index = i
for j in range(i+1, len(nums)):
if nums[min_index] > nums[j]:
min_index = j
if min_index != i:
nums[min_index], nums[i] = nums[i], nums[min_index]
def main():
nums = utils.get_random(0,100,10)
print("Raw input:")
utils.print_nums(nums)
select_sort(nums)
print("Result output:")
utils.print_nums(nums)
if __name__ == "__main__":
main()
时间复杂度
选择排序无论最好还是最坏的情况下,其比较次数一样多,第i趟排序需要n-i次比较,因此需要比较n-1+n-2+...+1 = n(n-1)/2次,对于交换次数,最好情况下,交换0次,最坏情况下交换n-1次,因此总的时间复杂度仍然是O(n^2)。
直接插入排序
将一个记录插入到已排序的序列当中。
c++
#include
#include
#include "utils.h"
using namespace std;
void InsertSort(IntArray &data)
{
IntArray temp;
for (ArrayIter input_iter = data.begin(); input_iter != data.end(); input_iter++)
{
if (temp.empty() || *input_iter > temp.back())
{
temp.push_back(*input_iter);
}
else
{
temp.push_back(INT_MIN);
ArrayIter output_iter;
// 终止条件比较复杂
for (output_iter = temp.end() - 1; *(output_iter - 1) > *input_iter && output_iter > temp.begin(); output_iter--)
{
*(output_iter) = *(output_iter-1);
}
*output_iter = *input_iter;
}
}
data = temp;
}
int main(int argc, char const *argv[])
{
IntArray data;
GetRandomArray(data, 0, 100, 10);
cout << "Raw input:" << endl;
PrintArray(data);
InsertSort(data);
cout << "Result output:" << endl;
PrintArray(data);
return 0;
}
python
import utils
def insert_sort(nums):
temp = []
for num in nums:
if len(temp) == 0 or num > temp[-1]:
temp.append(num)
else:
temp.append(num)
i = len(temp) - 2
while temp[i] > num and i > -1:
temp[i+1] = temp[i]
i -= 1
temp[i+1] = num
for i in range(len(nums)):
nums[i] = temp[i]
def main():
nums = utils.get_random(0,100,10)
print("Raw input:")
nums= [2,0,2,1,1,0]
utils.print_nums(nums)
insert_sort(nums)
print("Result output:")
utils.print_nums(nums)
if __name__ == "__main__":
main()
时间复杂度
最好情况下,即序列本身是有序的,无需移动,只需比较n次,因此时间复杂度为O(n);最坏情况下,即序列本身是逆序的,因此需要比较 2 + 3 + 4 + ... + n = (n+2)(n-1)/2次,记录的移动次数也达到最大值(n+4)(n-1)/2次,因此最大时间复杂度为O(n^2);平均时间复杂度约为n^2/4。
堆排序
堆是具有下列性质的完全二叉树,每个节点的值都大于或等于其左右孩子节点的值,成为大顶堆;或者每个几点的值小于或等于其左右孩子节点的值,称为小顶堆。
堆排序的具体过程为,将待排序的序列构成一个大顶堆,此时根节点一定是最大值,将根节点与尾节点进行交换,然后将剩余的n-1个序列重新构成一个堆,这样就可以得到n个元素中的次大值,如此反复执行,最后就构成一个有序序列。
c++
#include
#include "utils.h"
using namespace std;
void BuildSort(IntArray &data, int index, int len)
{
//置顶向下调整
for (int i = index; i < data.size();)
{
int left_child_index = 2 * i + 1;
int max_child_index = left_child_index;
if (left_child_index >= len)
{
//无子节点
break;
}
if (left_child_index + 1 < len && data[left_child_index + 1] > data[left_child_index])
{
max_child_index = left_child_index + 1;
}
if (data[i] > data[left_child_index])
{
//接下去的不用调整了
break;
}
else
{
//交换
int temp = data[max_child_index];
data[max_child_index] = data[i];
data[i] = temp;
}
i = max_child_index;
}
}
void HeapSort(IntArray &data)
{
for (int i = data.size() / 2 - 1; i >= 0; i--)
{
BuildSort(data, i, data.size());
}
for (int i = data.size(); i > 0; i--)
{
swap(data[0], data[i - 1]);
BuildSort(data, 0, i - 1); //是i-1而不是i
}
}
int main(int argc, char const *argv[])
{
IntArray data;
GetRandomArray(data, 0, 100, 100);
cout << "Raw input:" << endl;
PrintArray(data);
HeapSort(data);
cout << "Result output:" << endl;
PrintArray(data);
return 0;
}
python
import utils
#从heap_index往下重建堆
def build_heap(nums, heap_index, end):
while heap_index <=end:
left_index = 2 * heap_index + 1
right_index = 2 * heap_index + 2
max_child_index = left_index
#到堆底
if left_index > end:
return
if right_index <= end and nums[right_index] > nums[left_index]:
max_child_index = right_index
if nums[max_child_index] <= nums[heap_index]:
return
nums[heap_index],nums[max_child_index] = nums[max_child_index],nums[heap_index]
heap_index = max_child_index
def heap_sort(nums):
for heap_index in range(int(len(nums)/2) - 1, -1, -1):
# 初始重建需要从下往上建立
build_heap(nums, heap_index, len(nums) - 1)
for i in range(len(nums)-1, 0, -1):
nums[i], nums[0] = nums[0], nums[i]
#调整
build_heap(nums, 0, i-1)
def main():
nums = utils.get_random(0,100,10)
print("Raw input:")
utils.print_nums(nums)
heap_sort(nums)
print("Result output:")
utils.print_nums(nums)
if __name__ == "__main__":
main()
时间复杂度
构建堆的时间复杂度为O(n),每次重建对堆的需要用O(logn),需要取n-1次堆顶记录,因此时间复杂度为O(nlongn)。
归并排序
假设初始序列有n个记录,则可以看成是有n个有序的子序列,每个子序列的长度为1,然后两两归并,得到[n/2]个长度为2或为1的子序列,然后再两两归并,如此重复,直到一个长度为n的有序序列位置,这种成为2路归并排序。
c++
//递归版
#include
#include
#include "utils.h"
using namespace std;
void Merge(IntArray::iterator iter, uint32_t left, uint32_t mid, uint32_t right)
{
IntArray temp_array;
uint32_t left_index = left, right_index = mid + 1;
//比较
while (left_index <= mid && right_index <= right)
{
if (*(iter + left_index) < *(iter + right_index))
{
temp_array.push_back(*(iter + left_index));
left_index++;
}
else
{
temp_array.push_back(*(iter + right_index));
right_index++;
}
}
//将剩余的复制过去
while (left_index <= mid)
{
temp_array.push_back(*(iter + (left_index++)));
}
//将剩余的复制过去
while (right_index <= right)
{
temp_array.push_back(*(iter + (right_index++)));
}
//注意坐标的变化
int begin_index = 0;
while (begin_index + left <= right)
{
*(iter + left + begin_index) = temp_array[begin_index];
begin_index++;
}
}
void _MergeSort(IntArray::iterator iter, uint32_t left, uint32_t right)
{
if (left == right)
{
return;
}
uint32_t mid = (right + left) / 2;
_MergeSort(iter, left, mid); //递归归并排序
_MergeSort(iter, mid + 1, right);
Merge(iter, left, mid, right); //合并
return;
}
void MergeSort(IntArray &input_data)
{
_MergeSort(input_data.begin(), 0, input_data.size() - 1);
}
int main(int argc, char const *argv[])
{
const uint32_t TEST_NUM_COUNT = 10;
const int MIN_NUM = 0;
const int MAX_NUM = 100;
IntArray input_data;
GetRandomArray(input_data, MIN_NUM, MAX_NUM, TEST_NUM_COUNT);
cout << "Raw input:" << endl;
PrintArray(input_data);
MergeSort(input_data);
cout << "Raw input:" << endl;
PrintArray(input_data);
return 0;
}
//非递归版
#include
#include
#include "utils.h"
using namespace std;
//合并子序列
void Merge(IntArray &input, IntArray &output, int left, int mid, int right)
{
int left_index = left, right_index = mid + 1;
int start_index = left;
while (left_index <= mid && right_index <= right)
{
if (input[left_index] < input[right_index])
{
output[start_index++] = input[left_index];
left_index++;
}
else
{
output[start_index++] = input[right_index];
right_index++;
}
}
while (left_index <= mid)
{
output[start_index++] = input[left_index];
left_index++;
}
while (right_index <= right)
{
output[start_index++] = input[right_index];
right_index++;
}
}
void MergeSort(IntArray &input)
{
int len = (int32_t)(input.size()); //转化为有符号整型,防止下面计算的时候负数变为正整数(len-2*k -1)
IntArray output(input.size(), 0);
//k表示合并的子序列长度,大于len就无意义了,每次以2的倍数增长
for (int k = 1; k < len; k *= 2)
{
int l = 0;
//序号0开始, 一直到要合并的第二对合并子序列,因为最后一对可能长度不够,因此终止条件为 len-1 - 2*k
//如果恰好最后一对也是两个k序列,那么 刚刚len-1-2*k +2*k 为最后一个序号
for (l = 0; l <= len - 2 * k - 1; l += 2 * k)
{
Merge(input, output, l, l + k - 1 , l+2*k - 1 );
}
//l是最后一对要合并的序列的起始序号,如果剩余的序列长度>k要合并,否则不需要合并
if(len - l >= k)
{
Merge(input, output, l, l + k - 1, len - 1);
}
input = output;
}
}
int main(int argc, char const *argv[])
{
IntArray input_data, output_data;
GetRandomArray(input_data, 0, 100, 10);
cout << "Raw input:" << endl;
PrintArray(input_data);
MergeSort(input_data);
cout << "Result output:" << endl;
PrintArray(input_data);
return 0;
return 0;
}
python
#非递归
import utils
def _merge(nums, left, mid, right):
temp = []
left_index = left
right_index = mid+1
while left_index <= mid and right_index <= right:
if nums[left_index] <= nums[right_index]:
temp.append(nums[left_index])
left_index += 1
else:
temp.append(nums[right_index])
right_index += 1
while left_index <= mid:
temp.append(nums[left_index])
left_index += 1
while right_index <= right:
temp.append(nums[right_index])
right_index += 1
for index,num in enumerate(temp):
nums[left + index] = num
def _merge_sort(nums, left, right):
if left == right:
return
mid = int((left+right) / 2)
_merge_sort(nums, left, mid)
_merge_sort(nums, mid+1, right)
_merge(nums, left, mid, right)
def merge_sort(nums):
_merge_sort(nums, 0, len(nums)-1)
def main():
nums = utils.get_random(0,100,10)
print("Raw input:")
utils.print_nums(nums)
merge_sort(nums)
print("Result output:")
utils.print_nums(nums)
if __name__ == "__main__":
main()
#非递归
import utils
def _merge(nums, left, mid, right):
temp = []
left_index = left
right_index = mid+1
while left_index <= mid and right_index <= right:
if nums[left_index] <= nums[right_index]:
temp.append(nums[left_index])
left_index += 1
else:
temp.append(nums[right_index])
right_index += 1
while left_index <= mid:
temp.append(nums[left_index])
left_index += 1
while right_index <= right:
temp.append(nums[right_index])
right_index += 1
for index,num in enumerate(temp):
nums[left + index] = num
def merge_sort(nums):
k = 1 #子序列大小从1开始
while k < len(nums):
start = 0
while start <= len(nums) - 2*k :
_merge(nums, start, start + k - 1, start + 2*k -1)
start += 2*k
#剩余长度不足2k长度的序列
if len(nums) > start + k:
_merge(nums, start, start + k -1, len(nums) - 1)
k *= 2 #每次扩大到原来的2倍
def main():
nums = utils.get_random(0,100,10)
nums = [0,0,1,1,2,2]
print("Raw input:")
utils.print_nums(nums)
merge_sort(nums)
print("Result output:")
utils.print_nums(nums)
if __name__ == "__main__":
main()
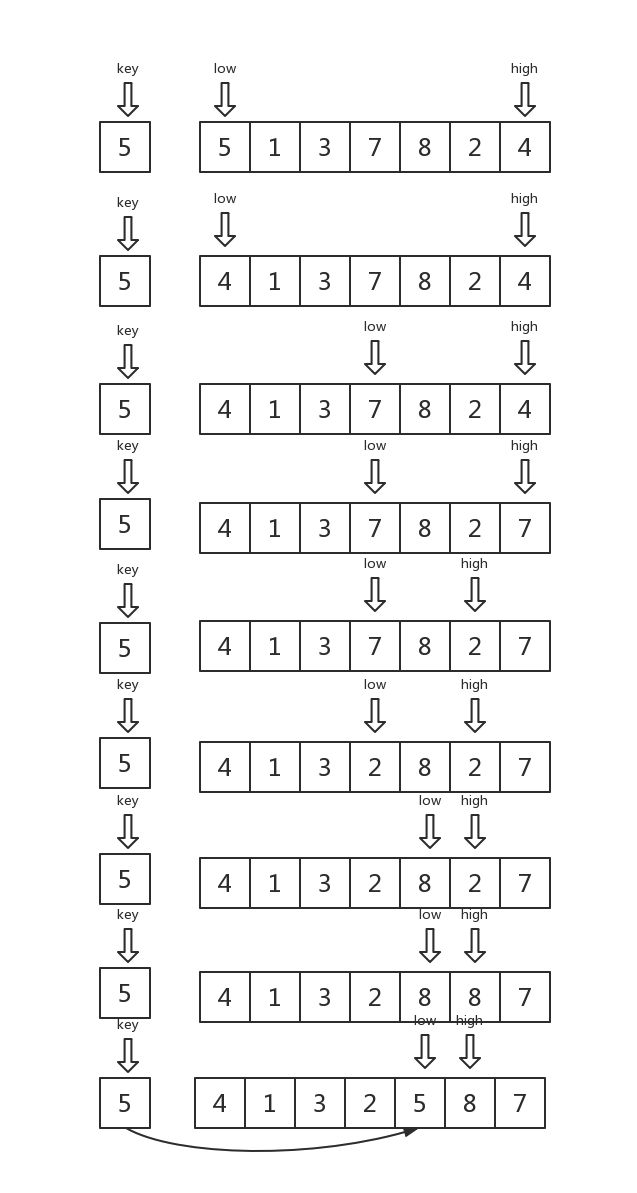
快速排序
对于一个顺序的序列来说,对于其中的每一个数字,它左边的数字总是小于或等于它,它右边的数字总是大于或等于它,根据这个思想,提出了快速排序的概念。
基本思想是通过一趟排序将待排序的记录分割成独立的两部分,其中一部分记录的关键字比另一个部分的关键字小,则可分别对这两部分记录进行排序,已达到整体有序的目的。
c++
#include
#include "utils.h"
using namespace std;
void Partition(IntArray &input, int low, int high, int &partition_index)
{
int key = input[low];
while (low < high)
{
//找到右侧小于key的值
while (low < high && input[high] > key)
{
high--;
}
//移动到左边
if (low < high)
{
int temp = input[low];
input[low] = input[high];
input[high] = temp;
}
//寻找左边大于key 的值
while (low < high && input[low] <= key)
{
low++;
}
//移动到右边
if (low < high)
{
int temp = input[low];
input[low] = input[high];
input[high] = temp;
}
//low~hight又是跟初始状态一样,再继续寻找
}
partition_index = low;
}
void QSort(IntArray &input, int low, int high)
{
if (low >= high)
{
return;
}
int partition_index = -1;
/*
原理:元素在排序中所在的位置,之前的元素都比该元素小,之后的元素都比该元素大
因此快排的原理就是寻找位置,使得之前的元素比该值小,之后的元素比该值大
*/
Partition(input, low, high, partition_index);
QSort(input, low, partition_index - 1);
QSort(input, partition_index + 1, high);
}
void QuickSort(IntArray &input_data)
{
int low = 0;
int high = input_data.size() - 1;
QSort(input_data, low, high);
}
int main(int argc, char const *argv[])
{
IntArray input_data, output_data;
GetRandomArray(input_data, 0, 100, 10);
cout << "Raw input:" << endl;
PrintArray(input_data);
QuickSort(input_data);
cout << "Result output:" << endl;
PrintArray(input_data);
return 0;
return 0;
}
python
import utils
import time
def _partitions(nums, low, high):
key = nums[low]
while low < high:
while low < high and nums[high] >= key:
high -= 1
if low < high:
nums[low] = nums[high]
while low < high and nums[low] <= key:
low += 1
if low < high:
nums[high] = nums[low]
nums[low] = key
return low
def _quick_sort(nums, low, high):
if low >= high: #条件为大于或等于
return
partition_index = _partitions(nums, low, high)
_quick_sort(nums, low, partition_index)
_quick_sort(nums, partition_index+1, high)
def quick_sort(nums):
_quick_sort(nums, 0, len(nums) - 1 )
def main():
nums = utils.get_random(0,100,10)
print("Raw input:")
utils.print_nums(nums)
quick_sort(nums)
print("Result output:")
utils.print_nums(nums)
if __name__ == "__main__":
main()
总结
| 排序方法 | 平均复杂度 | 最好情况 | 最坏情况 | 辅助空间 | 稳定性 |
|---|---|---|---|---|---|
| 冒泡 | O(n^2) | O(n) | O(n^2) | O(1) | 稳定 |
| 选择排序 | O(n^2) | O(n^2) | (n^2) | O(1) | 稳定 |
| 插入排序 | O(n^2) | O(n) | O(n^2) | O(n) | 稳定 |
| 堆排序 | O(nlogn)~O(n^2) | O(n^1.3) | O(n^2) | O(1) | 不稳定 |
| 归并排序 | O(nlogn) | O(nlogn) | O(nlogn) | O(n) | O(n) 不稳定 |
| 快速排序 | O(nlogn) | O(nlogn) | O(n^2) | O(logn)~O(n) | 不稳定 |