matlab RBF 神经网络拟合
(1)newrb()
https://www.mathworks.com/help/deeplearning/ref/newrb.html
该函数可以用来设计一个近似径向基网络(approximate RBF)。调用格式为:
[net,tr]=newrb(P,T,GOAL,SPREAD,MN,DF)
其中P为Q组输入向量组成的R*Q位矩阵,T为Q组目标分类向量组成的S*Q维矩阵。GOAL为均方误差目标(Mean Squard Error Goal),默认为0.0;SPREAD为径向基函数的扩展速度,默认为1;MN为神经元的最大数目,默认为Q;DF维两次显示之间所添加的神经元数目,默认为25;ner为返回值,一个RBF网络,tr为返回值,训练记录。
用newrb()创建RBF网络是一个不断尝试的过程(从程序的运行可以看出来),在创建过程中,需要不断增加中间层神经元的和个数,知道网络的输出误差满足预先设定的值为止。
(2)newrbe()
https://www.mathworks.com/help/deeplearning/ref/newrbe.html
该函数用于设计一个精确径向基网络(exact RBF),调用格式为:
net=newrbe(P,T,SPREAD)
其中P为Q组输入向量组成的R*Q维矩阵,T为Q组目标分类向量组成的S*Q维矩阵;SPREAD为径向基函数的扩展速度,默认为1
和newrb()不同的是,newrbe()能够基于设计向量快速,无误差地设计一个径向基网络。
(3)radbas()
该函数为径向基传递函数,调用格式为
A=radbas(N)
info=radbas(code)
其中N为输入(列)向量的S*Q维矩阵,A为函数返回矩阵,与N一一对应,即N的每个元素通过径向基函数得到A;info=radbas(code)表示根据code值的不同返回有关函数的不同信息。包括
derive——返回导函数的名称
name——返回函数全称
output——返回输入范围
active——返回可用输入范围
使用exact径向基网络来实现非线性的函数回归:
%%清空环境变量
clc
clear
%%产生输入输出数据
%设置步长
interval=0.01;
%产生x1,x2
x1=-1.5:interval:1.5;
x2=-1.5:interval:1.5;
%按照函数先求的响应的函数值,作为网络的输出
F=20+x1.^2-10*cos(2*pi*x1)+x2.^2-10*cos(2*pi*x2);
%%网络建立和训练
%网络建立,输入为[x1;x2],输出为F。spread使用默认
net=newrbe([x1;x2],F);
%%网络的效果验证
%将原数据回带,测试网络效果
ty=sim(net,[x1;x2]);
%%使用图像来看网络对非线性函数的拟合效果
figure
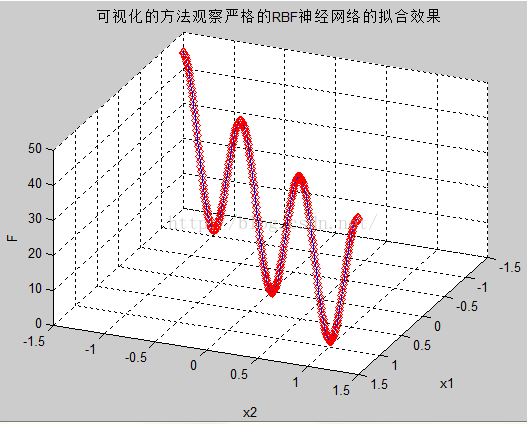
plot3(x1,x2,F,'rd');
hold on;
plot3(x1,x2,ty,'b-.');
view(113,36);
title('可视化的方法观察严格的RBF神经网络的拟合效果');
xlabel('x1')
ylabel('x2')
zlabel('F')
grid onapproximate RBF网络对函数进行拟合
%%清空环境变量
clc
clear
%%产生训练样本,训练输入,训练输出
%ld为样本隶属
ld=400;
%产生2*ld的矩阵
x=rand(2,ld);
%将x转换到[-1.5 1.5]之间
x=(x-0.5)*1.5*2;
%x的第一行为x1,第二行为x2
x1=x(1,:);
x2=x(2,:);
%计算网络输出F值
F=20+x1.^2-10*cos(2*pi*x1)+x2.^2-10*cos(2*pi*x2);
%%建立RBF神经网络
%采用approximate RBF神经网络,spread为默认值
net=newrb(x,F);
%%建立测试样本
interval=0.1;
[i,j]=meshgrid(-1.5:interval:1.5);
row=size(i);
tx1=i(:);
tx1=tx1';
tx2=j(:);
tx2=tx2';
tx=[tx1;tx2];
%%使用建立的RBF网络进行模拟,得出网络输出
ty=sim(net,tx);
%%使用图像,画出三维图
%真正的函数图像
interval=0.1;
[x1,x2]=meshgrid(-1.5:interval:1.5);
F=20+x1.^2-10*cos(2*pi*x1)+x2.^2-10*cos(2*pi*x2);
subplot(1,3,1);
mesh(x1,x2,F);
zlim([0,60]);
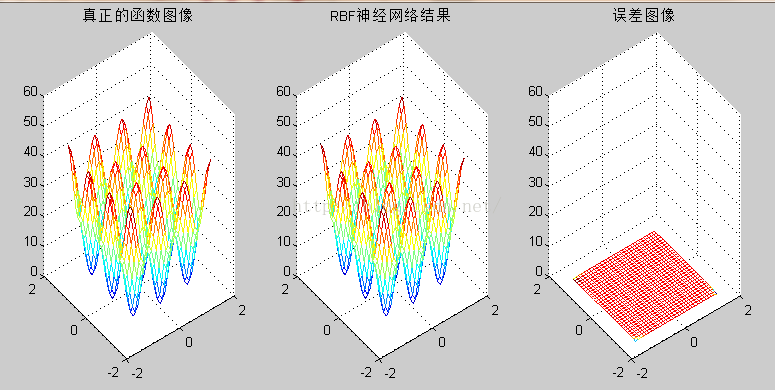
title('真正的函数图像');
%网络得出的函数图像
v=reshape(ty,row);
subplot(1,3,2);
mesh(i,j,v);
zlim([0,60]);
title('RBF神经网络结果');
%误差图像
subplot(1,3,3);
mesh(x1,x2,F-v);
zlim([0,60]);
title('误差图像');
set(gcf,'position',[300,250,900,400])结论:可以看出神经网络的训练结果能够较好逼近该非线性函数F,由误差图可知,实景网络的预测效果在数据边缘处的误差较大,在其它书指出的拟合效果很好,网络的输出值与函数值之间的插值在隐藏层神经元的个数为100时已经接近0,说明网络输出能非常好地逼近函数。
![]()