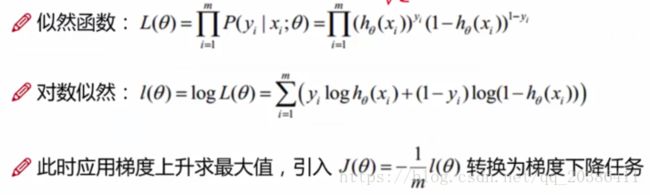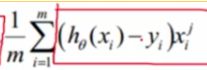LR逻辑回归

LR逻辑回归

先看线性回归，sigmoid函数中的z就是线性回归的内容。线性回归带入SIGMOD函数

目的：

训练出0/1分类器

步骤

想到sigmoid函数中的概率→目标函数P(y|θ,x)，hθ(x)→求θ，取似然函数，取对数L(θ)→max(L(θ))→min((L(θ)))→求偏导，另偏导为0

 

线性回归的升级

虽然叫回归，但是是最厉害的二分类算法

非线性就是高阶（视频解释）

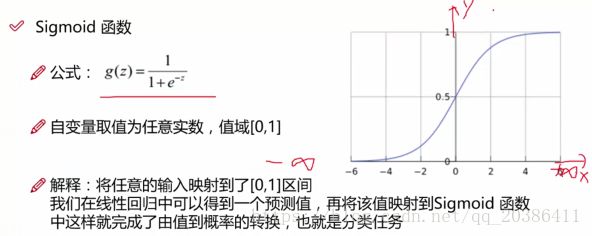
由输入到概率的转化

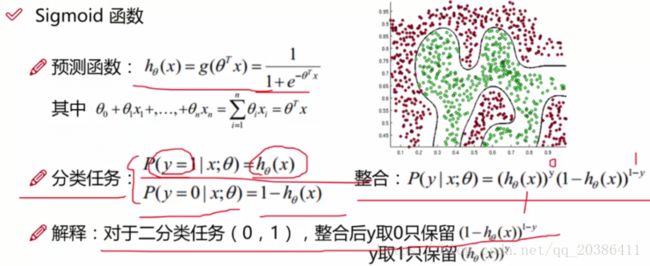
y表示分类为0还是1，h(x)表示概率

把特征的线性组合带入sigmoid函数得到y=1的概率

线性回归里面的标签y为连续值，在最小二乘法的被减数上；LR中的标签为0,1，在幂次上

用每一个机器学习模型都要弄清楚目标函数是什么

为了让结果值最符合数据，写出整合表达式对应的似然函数，根据似然函数求出最合适的参数

求对数似然的最大值，这是梯度上升问题，而常规操作时处理梯度下降问题。1/m，表示综合考虑m个样本

目标函数/损失函数是什么？

偏导结果可以凑成（这一这个小技巧）

偏导更新的方向已经求出

有多少个θ就求多少次偏导，这里直接用θj表示所有的偏导（每个特征都对应一个j，说明有j个特征）

xij表示第i个样本的第j个特征（某一行数据中的那列数据）。i表示第几个样本，j表示此样本的第j个特征

 

根据对数似然知要求出最大值，通常方法是求解最小值，于是把似然函数取负值再求解（梯度上升转梯度下降）

是梯度下降的目标函数

步长乘方向即为更新的幅度，前面的负号表示用梯度下降做的，这样就得到了所有θ

求偏导的结果为更新的方向（偏导方向），步长α（学习率，控制更新速度）乘方向为结果值（更新幅度），m表示综合考虑m个样本

θ不断更新，每迭代一次更新一次，θ=θ-α*grad，直到得到最终的θ

 

实例：根据学生的两门成绩判断该学生是够能被某大学录取

目标：建立分类器，求解三个参数，即θ0（偏置项）θ1（第一门成绩的参数）θ2（第二门成绩的参数）

设定阈值，根据阈值判断录取结果

np.random.shuffle()洗牌操作，打乱数据顺序

cost目标函数（纵轴），随着不断迭代（横轴），cost会下降到稳定值（收敛）

head()函数打印前5行数据

 

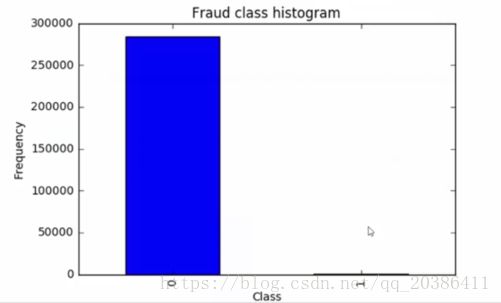
实例：信用卡欺诈检测

0正常，1异常，即标签y

数据为28个特征（已经进行预处理）的的多行数据

 

样本不均衡问题：正负样本的比例，面试问到

样本不均衡怎么做，如大多是正常数据，很少的异常数据

过采样（over sample）：同样多。生成一些1样本数据，使1和0的样本数量一样多。首选方法，数据肯定是越多越好

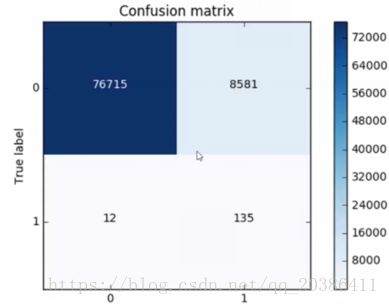
优点：误判的数据减少（因为所有的正常数据都被拿来训练了），右上的数据（0预测为1，即错判）会比下采样小10倍（与下图相比）

recall=TP/(TP+FN)，FN表示正例被预测成负例，在此处表示将真实标签0被预测为1，即右上角表示的数，而这个在下采样是非常大的，在过采样中是非常小的

横轴为预测标签

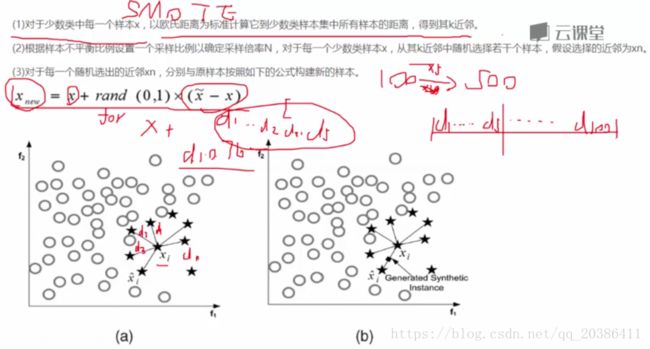
生成数据方法：SMOTE算法

训练集生成数据，生成数据与测试集无关

下采样（under sample）：同样少。0多1少，从0中选取和1相同数量的样本

缺点：用了少量数据训练模型，结果导致过拟合。将本来正常的数据0误判为数据1，这个误判的数据个数会增多（原来很大部分没有用来训练的的数据输入模型后发生错判，正常0被误判有欺诈1的情况增多）

下采样对应的混淆矩阵：下面的数据只包含采样后的数据，上面的数据包含所有的数据

横轴为预测标签

 

交叉验证:用于模型评估找出最好的参数（不同的参数对应的模型召回率和精度有很大区别）

数据切分为训练集和测试集

训练出的模型会包含很多参数，这些参数选大的好还是选小的好？

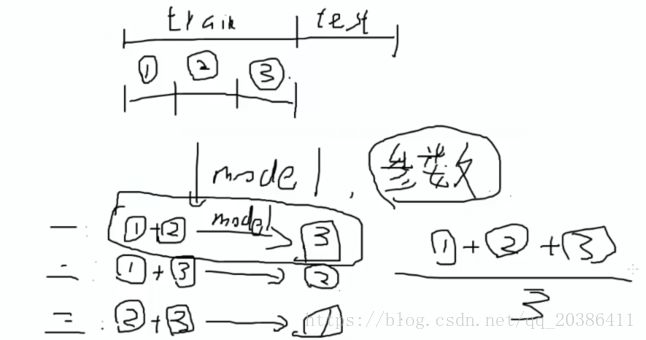
通过交叉验证来确定出参数：再将训练集再分为3段

1和2训练模型，3验证模型

1和3训练模型，2验证模型

2和3训练模型，1验证模型

K交叉验证（KFold），训练集切分为3份，K值为3；训练集切分为5份，K值为5

根据交叉验证模型的最终评估值cross_val_score来决定用哪个参数

 

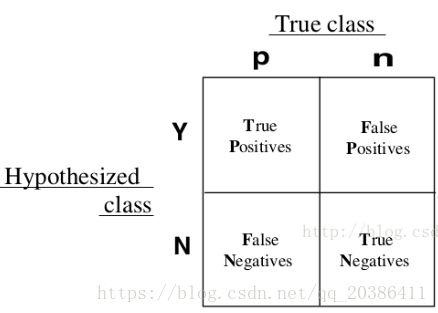
模型评估的几个指标

TP和TN是拿挑出的样本来看的： 

TP：判断正确了，且判断为正例（挑出样本中，女判为女）

FP：判断错误了，且判断为正例（挑出样本中，男判为女）

这个图没有理解？横纵表示什么含义？

准确：对的错的都包括

精准：只看对的

 

 

正则化：两种 ，L1（|w|）和L2（1/2w^2），上面求出的目标/损失函数需要加一些额外的项

加上正则化项目的：可以更好的选择合适的参数，正则化能对结果产生很大的影响

加上正则化去惩罚目标函数（本来是希望目标函数越小越好的，现在加了一项，相当于惩罚了目标函数，但是可以判断出那个模型效果更好了）

通过梯度下降方法求出每个特征最合适的权重参数θ

现在通过交叉验证得到如上图A，B两个模型，假设这两个模型的recall值都为90%，那应该选择哪一个模型？

可以画出θ参数的分布

选择的θ要使模型的泛化能力更强（不仅仅表现在训练数据，在测试数据上的效果也要很好），θ浮动越小，过拟合的风险越低，因此选择θ浮动较小的权重参数

 

现在就用惩罚项大力度的惩罚A模型，小力度的惩罚B模型

 

λ：惩罚力度，一般是λL1，λL2，这里λ就可以取很多值，根据交叉验证选出最合适的值

数据需要标准化的原因：模型会认数值大的的特征重要程度比较大，所以数据要进行标准化

 

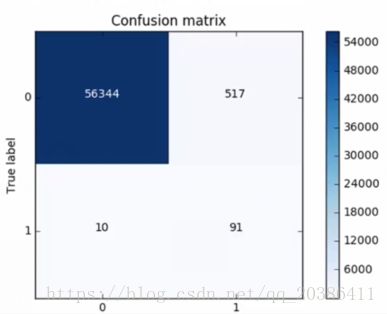
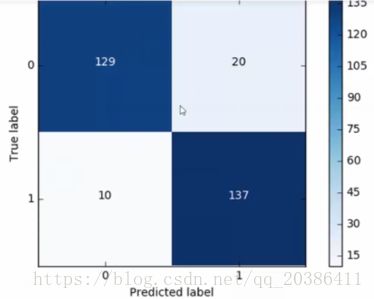
混淆矩阵：下采样数据情况下计算

背景：1是正例，0是负例

Recall=TP/(TP+FN)=137/(137+10)  注意这个图纵轴是从1开始的（recall需要先弄清楚0表示正例还是1表示正例，这里的例子背景与上面的就不同）

注：FN（左下部分）表示预测错了，预测成负例，即真实标签为1预测成0（横纵轴含义，真实标签和预测标签都是已知的）。也可以理解为没有被找出来的数据，本来标签为1，但是预测成0，即没有找出来

精度=（0预测为0+1预测为1）/all=(129+137)/all

注：奢侈品广告投放给奢侈品用户，模型分类准确率达到95%，但在实际过程中，还是把大部分广告投放给非奢侈品用户？

这个问题就是用精度作为模型评估的缺点

当负样本占99%时，分类器把所有样本预测为负样本也可以获取99%的准确率。样本比例非常不均衡是，占比达的类别往往会成为影响准确率的最主要因素

当奢侈品用户只占全体用户的一小部分，虽然模型分类准确率很高，不代表对奢侈品用户的分类准确率也很高

解决：平均准确率，每个类别下的样本准确率的平均作为模型评估的指标

 

LR阈值选择对Recall影响（人为控制模型效果）：

默认为0.5

当阈值为0.1，会使所有样本预测值和原始标签值相同，即都会被预测为正例，其中FN表示将正例预测成负例的个数，显然FN这个值为0，recall会接近1

阈值不断增大，recall会不断减小

还需要再原始的数据集上操作，即下采样中没有用到的原始数据：