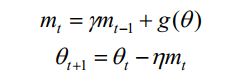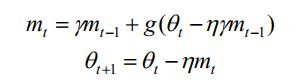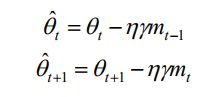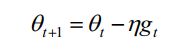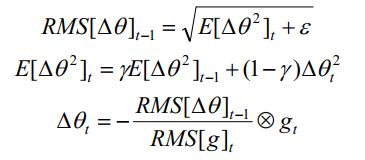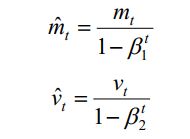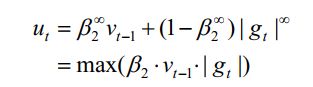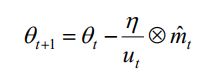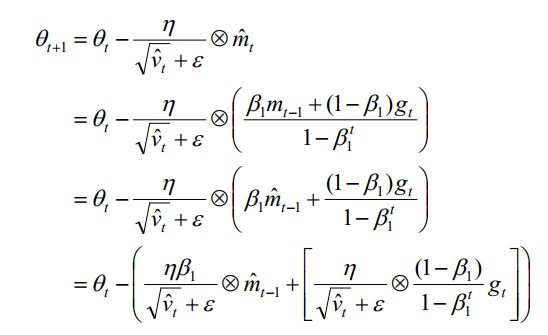【深度学习】1、常见模型优化算法原理与项目实践对比(PyTorch实践)
目录
简介
1、SGD(Stochastic Gradient Descent, SGD)
2、Momentum
3、NAG(Nesterov Accelerated Gradient,NAG)
4、Adagrad
5、RMSProp
6、Adadelta
7、Adam
8、AdaMax
9、Nadam
10、优化算法的使用
11、训练笔记
优化实践对比
简介
在传统的机器学习算法的实践中,优化总是重头戏,也是最考验功底的部分。深度学习得益于传统的有效方式,往往普通的随机下降优化算法就能取得不错的训练效果,优化的重要性相比于传统机器学习要弱一些,大部分从业者主要聚焦于应用或模型创新,而优化部分更多的工作只是调参。
实际上,深度学习优化方面的研究非常多,很多方法也非常有效,尤其在数据量比较大的时候,所以有必要掌握一些常见的优化算法。
1、SGD(Stochastic Gradient Descent, SGD)
随机梯度下降(Stochastic Gradient Descent, SGD)每次训练样本随机抽取一个样本计算loss和梯度并对参数进行更新,由于每次不需要遍历所有的数据,所以每次迭代速度快;但是这种优化算法比较弱,往往容易走偏,反而会增加很多次的迭代。随机梯度下降法有时可以用于在线学习(Online Learning)系统,可使系统快速学习到新的变化。
与随机梯度下降算法对应的还有批量梯度下降(Batch Gradient Descent,BGD),每次使用整个训练集合计算梯度,这样计算的梯度比较稳定,相比随机梯度下降法不那么容易振荡,但是因为每次都需要更新整个数据集,所以批量梯度下降法非常慢,而且无法放在内存中计算,更无法应用于在线学习系统。
介于随机梯度下降法和批量随机梯度下降法之间的是小批量随机梯度下降法(Mini-Batch Gradient Descent),即每次随机抽取m个样本,以它们的梯度均值作为梯度的近似估计值。
为了使得随机梯度下降获取更好的性能,学习率需要取值合理,并根据训练过程动态调整。如果学习率过大,模型就会收敛过快,最终离最优值较远;如果学习率较小,迭代次数就会很多,导致模型长时间不能收敛。
2、Momentum
动量(Momentum)是来自物理学中的定义,是力的时间积累效应的度量。动量的方法在随机梯度下降的基础上,加上了上一步的梯度:
其中γ是动量参数且γ∈[0,1]。动量的优化方法也可以写成如下的形式:
由于上面两种的表达方式是一致的,所以选择第一种的表达方式。
相比于随机梯度下降,动量会使相同方向的梯度不断累加,而不同方向的梯度则相互抵消,因而可以一定程度上客服“Z”字形的振荡,更快到达最优点。
3、NAG(Nesterov Accelerated Gradient,NAG)
Nesterov 加速梯度于动量类似,也是考虑最近的梯度的情况,但是NAG相对超前一点,它先使用动量mt计算参数θ下一个位置的近似值θ+ηmt,然后在近似位置上计算梯度:
NAG与动量法的区别就是,NAG算法会计算本轮迭代时动量到达的位置的梯度,可以说成“未来”的梯度。如果未来的梯度存在一定的规律,那么这些梯度就会有更好的利用价值。
在实际的应用中,为了前向、后向计算统一,引入以下爱的变量:
将上面的两个公式代入,可以得到:
将上面的第一个公式代入第二个公式,就可以得到:
整理可以得到:
这样梯度计算就可以解决计算不一致的问题。
4、Adagrad
Adagrad是一种自适应的梯度下降法,它能够针对参数更新的频率调整它们的更新幅度——对于更新频繁且更新量大的参数,适当减小他们的步长;对于更新不频繁的参数,适当增大它们的步长。这种方法的思想很适合一些数据分布不均匀的任务。
具体的方法就是在之前的梯度下降法的基础上增加一个梯度的累积项作为分母,之前的梯度下降法的更新公式为:
而Adagrad变成:
其中⊙表示向量之间元素级的乘法,Gt就是Adagrad增加的内容。它是所有轮迭代的梯度平方和:
从公式可以看出,加入这一下项以后,参数的更新确实得到了一定的控制。对于经常更新的参数,Gt项的数值会比较大,因而它的参数更新量会得到控制;对于不经常更新的参数,由于Gt项的数值比较小,它的参数更新量会变大。
从算法里面可以看出,Adagrad依然存在一些缺陷,如果模型的参数数值保持稳定,那么参数的梯度值总体不会有太大的波动,而分母上的梯度积累项一直在积累,因此分母会不断变大,因此从梯度的趋势上分析,梯度总值会不断减小。虽然在实际训练中一般也会将学习率调小,但两者变小的程度不同,因此Adagrad可能会出现更新量太小而不易优化的情况。
5、RMSProp
RMSProp利用滑动平均的方法来解决Adagrad算法中的问题。它的思路是让梯度积累值G不要一直变大,而是按照一定的比例衰减,这样其含义就不再是梯度的积累项了,而是梯度的平均值:
因为此时的G更像是梯度的平均值甚至期望值,因此在很多文献中会将G写成E[g2]。
6、Adadelta
Adadelta考虑了一些更新量“单位”的问题。为了让“单位”匹配,Adadelta选择在分子上再增加一个项目,于是方法的概念公式变成:
其中RMS表示Root Mean Square,也就是“均方根”的意思。分母中的RMS[g]t展开与RMSProp相同:
分子采取类似的方法,展开后可以得:
7、Adam
Adam算法的全称是Adaptive Moment Estimation,这种方法结合了上面提到的两类算法:基于动量的算法和基于自适应的算法。基于动量的算法有动量法和NAG法,这两种方法都基于历史梯度信息进行参数更新。基于自适应学习率的算法有Adagrad、RMSProp、Adadelta,它们通过计算梯度的累计信息量来调整不同参数的更新量。Adam算法记录了梯度的一阶矩(梯度的期望)和二阶矩(梯度平方的期望):
为了确保两个梯度累积量能够良好的估计梯度的一阶矩和二阶矩,两个累积量还需要乘以一个偏置纠正的系数:
然后再使用两个累积量进行参数更新:
完整伪代码:
8、AdaMax
AdaMax算法主要是针对Adam算法进行了修改,而修改的位置在二阶矩v这里。AdaMax将二阶矩修改为无穷矩,这样在数值上更加稳定:
将vt替换为ut后,最终的更新变为:
此时的无穷矩估计不再是有偏的,因此也不需要再做纠正。最终的伪代码如下:
9、Nadam
与AdaMax具有类似的思想,Nadam算法修改的是一阶矩的估计值,将Nesterov算法和Adam算法的结合,形成了Nadam(Nesterov-Accelerated Adaptive Moment Estimate)算法。
NAG算法的计算公式为:
Adam更新的公式可以展开为:
可以看出,公式形式和NAG很接近,为了体现Nesterov的效果,只需将公式中的mt-1修改为mt即可。
10、优化算法的使用
优化算法分为两类:其中一类是以动量为核心的算法;另一类以自适应为核心的算法。
以动量为核心的算法更容易在山谷的优化曲面中找到最优解,如果优化曲面在某个地方振荡严重,而在另外一些方面趋势明显,那么基于动量的算法能够把握这种趋势,让又趋势的方向累积能量,同时让振荡的方向相互抵消;基于动量的方法如果遇到趋势不明显的情况,那么优化参数的路径必然会存在一些绕弯的情况;
以自适应为核心的算法容易在各种场景下找到平衡,对于梯度较大的一些场景,它会适当地减少更新量;而对于梯度较小的一些场景,它会适当增加更新量,所以实际上是对优化做了一定的折中。当然,对于一些复杂且难以优化的问题来说,这样的限制实际上阻碍了优化的快速进行。
当然,理论上结合两者的算法效果应该更好,因此Adam以及它的一些改进算法的效果通常不错,但是其计算量也会增加,这一点在使用时要权衡考虑。
11、训练笔记
(1)对于稀疏数据,尽量使用学习率可自适应的优化方法,不用手动调节,而且最好采用默认值;
(2)SGD通常训练时间更长,但是在好的初始化和学习率训练方案下,结果更加可靠;
(3)如果在意更快收敛,并且需要训练较复杂的网络时,尽量使用自适应的优化方法;
(4)Adadelta、RMSProp、Adam是比较相近的算法,在相似的情况下表现差不多;
(5)在想使用动量的RMSProp或者Adam的地方,大多可以使用Nadam取得更好的效果。
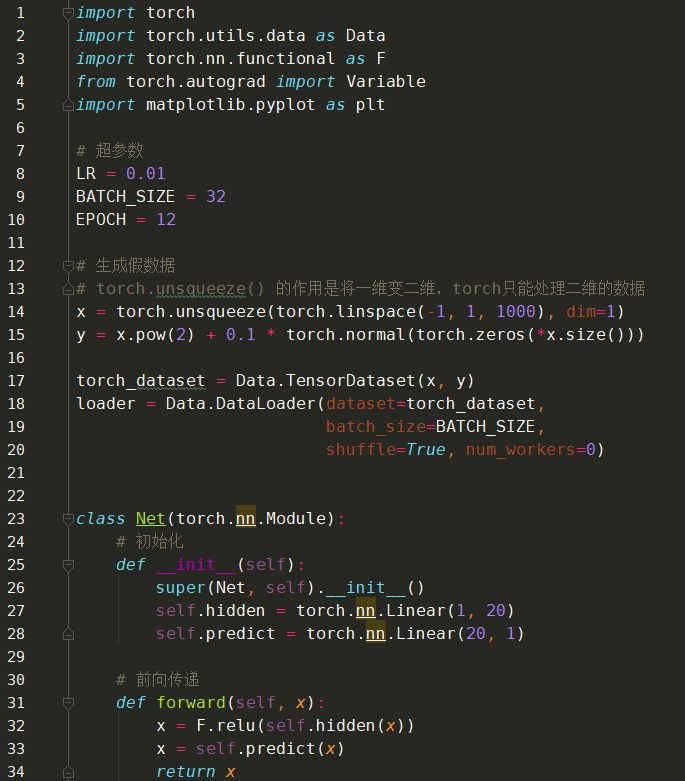
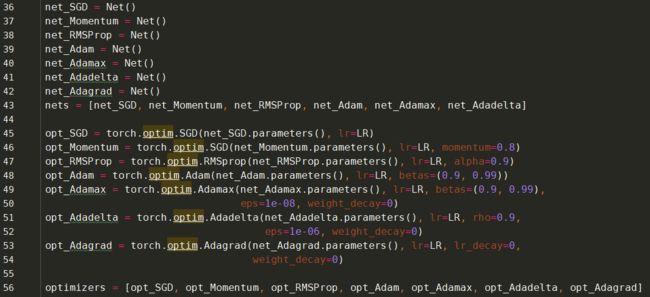
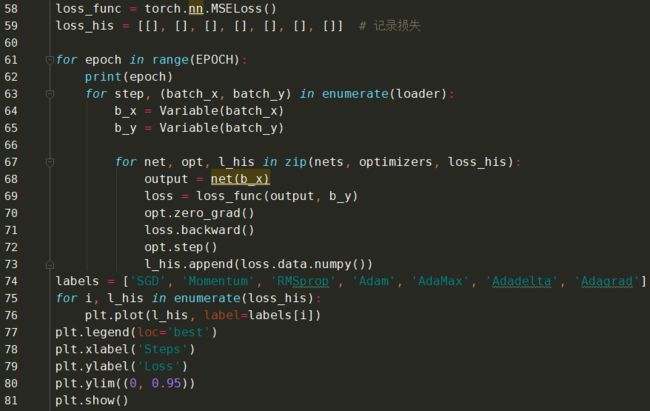
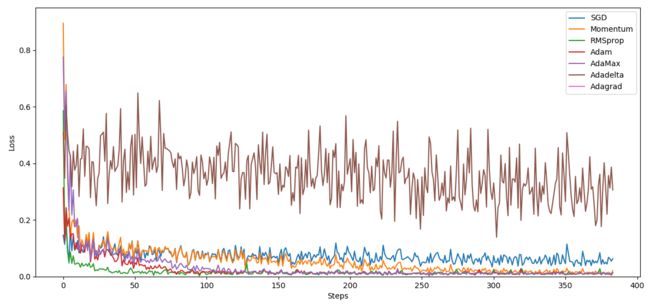
优化实践对比
执行结果:
公众号回复【优化算法】即可获取该文章的PDF文件和项目实践代码,也非常期待您的打赏。
参考:
PyTorch的十个优化器:
https://blog.csdn.net/u011995719/article/details/88988420
《深度学习核心技术与实践》
声明:转载请说明出处
下方为小生公众号,还望包容接纳和关注,非常期待与您的美好相遇,让我们以梦为马,砥砺前行。
希望技术与灵魂可以一路同行
长按识别二维码关注一下更多精彩内容可回复关键词每篇文章的主题即可
![]()
![]()