计算机视觉教程核心版(六)数据预处理、初始化和分类与回归
数据预处理、权重初始化和损失函数
- warming up
- 数据预处理
- 权重初始化
- 学习率初始化
- 正则化
- 总结
warming up
在之间的章节中。我们介绍了神经元的模型,其计算点乘后跟着一个非线性化,而神经元排列成层。合并起来,不同的层数、每层不同神经元的个数以及不同的激活函数定义了新型的得分函数(从线性映射扩展得来)。在本节中,我们将讨论其他针对数据预处理、权重初始化和损失函数的设计选择。

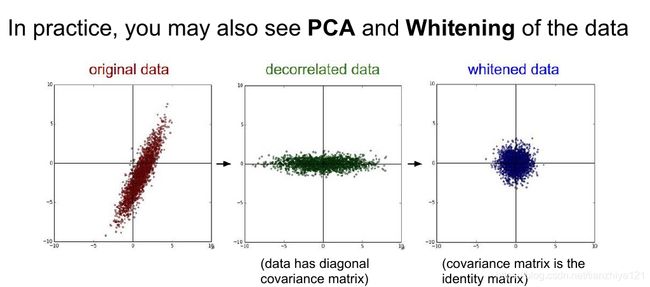
在实际中并不常用标准化方差,PCA或者白化。另外预处理操作仅仅作用于训练数据,之后运用于验证集和测试集合,即均值必须现在整个训练集上计算出来,之后被训练集、验证集和测试集减去。
数据预处理
我们假设输入矩阵的size[N*D],N是数据的数量,D是它们的维度。
均值相减是最常用的预处理方法。操作方法是将数据集上的每个特征值减去均值,其几何解释是将数据云在每一个维度都以原点为中心。在numpy中这个操作的执行代码如下:
x -= np.mean(x, axis = 0)
特别地,对于图像为了方便经常将所有的像素值减去均值(AlexNet),或者将图像通道分离,减去每个通道的均值(VGGNet)
权重初始化
我们已经学习了如何构建一个神经网络,和如何预处理数据。在我们开始训练神经网络之前,我们还必须初始化参数。
注意
不要将所有的权重初始化为零。如果这样做,将导致所有的神经元计算同样的输出,之后他们将计算出同样的梯度,所有的神经元将经手相同的梯度更新。换句话说,神经元的之间的权重对称行没有解决。
如果你观察损失函数如图示例:
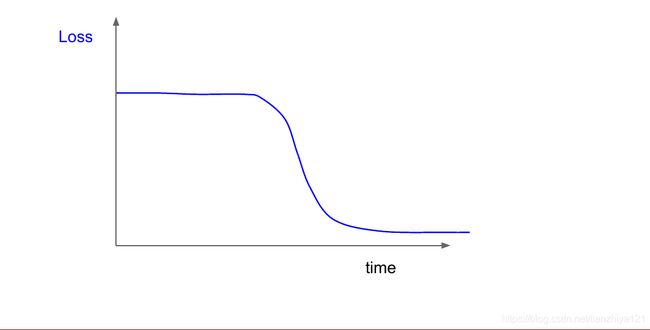
在上图中,损失函数在初期几乎没有变化,之后一段时间开始下降,这表明在初期权重初始化并不好。
小而随机的数字:一般情况下,我们希望权重接近于零,但是又不是完全是零。因此,常用的一种做法是使用较小的数字初始化神经元权重,以此对称破碎。这样做的思想是,神经元全初始都是随机和独立,因此它们将计算独立的更新并且最终作为给的不同的部分混入神经网络中。
注意,不一定越小的初始权重就越好。例如较小的权重初始化可能会导致反向传播时候,有很小的梯度,进而导致梯度消失问题。
使用1/sqrt(n)校准方差。上述问题的一个建议是零w=np.random.rand(n)/sqrt(n)
更多相关内容
properties of variance
Understanding the difficulty of training deep feedforward neural networks
Delving Deep into Rectifiers: Surpassing Human-Level Performance on ImageNet Classification
实际中常用w = np.random.randn(n) * sqrt(2.0/n)和Relu参见 He et al…
批标准化(batch normalization)是在神经网路的每一层的预处理。它在神经网络中的使用很常见,一般用于全连接层和卷积层之后。更多Batch Normalization
学习率初始化
对于学习率的设置一般初始设置为[1e-3,1e-5]之间,具体视情况而定。如果你发现该训练中的损失几乎不改变,则可能是学习率设置太低的原因进而导致梯度几乎不更新。然而在损失几乎不变的情况下,依然可以出现准确率提升的现象,这表明权重参数正在朝正确的方向前进。如果你的训练中出现了损失Nan,这表明你的学习率太大,需要降低学习率。
示例如下
正则化
控制神经网络过拟合有多种方法
常见的添加项的正则化方法有L2 regularization、L1 regulization,对于它们的作用由很多争议。一种更为常见的方法是Dropout方法。Dropout方法通过随机概率仅仅保留一部分神经元出于激活状态。如图
""" Vanilla Dropout: Not recommended implementation (see notes below) """
p = 0.5 # probability of keeping a unit active. higher = less dropout
def train_step(X):
""" X contains the data """
# forward pass for example 3-layer neural network
H1 = np.maximum(0, np.dot(W1, X) + b1)
U1 = np.random.rand(*H1.shape) < p # first dropout mask
H1 *= U1 # drop!
H2 = np.maximum(0, np.dot(W2, H1) + b2)
U2 = np.random.rand(*H2.shape) < p # second dropout mask
H2 *= U2 # drop!
out = np.dot(W3, H2) + b3
# backward pass: compute gradients... (not shown)
# perform parameter update... (not shown)
def predict(X):
# ensembled forward pass
H1 = np.maximum(0, np.dot(W1, X) + b1) * p # NOTE: scale the activations
H2 = np.maximum(0, np.dot(W2, H1) + b2) * p # NOTE: scale the activations
out = np.dot(W3, H2) + b3
Dropout方法一般在训练时候使用,由于测试时候的表现非常重要,通常更倾向于使用翻版的Dropout,代码如下
"""
Inverted Dropout: Recommended implementation example.
We drop and scale at train time and don't do anything at test time.
"""
p = 0.5 # probability of keeping a unit active. higher = less dropout
def train_step(X):
# forward pass for example 3-layer neural network
H1 = np.maximum(0, np.dot(W1, X) + b1)
U1 = (np.random.rand(*H1.shape) < p) / p # first dropout mask. Notice /p!
H1 *= U1 # drop!
H2 = np.maximum(0, np.dot(W2, H1) + b2)
U2 = (np.random.rand(*H2.shape) < p) / p # second dropout mask. Notice /p!
H2 *= U2 # drop!
out = np.dot(W3, H2) + b3
# backward pass: compute gradients... (not shown)
# perform parameter update... (not shown)
def predict(X):
# ensembled forward pass
H1 = np.maximum(0, np.dot(W1, X) + b1) # no scaling necessary
H2 = np.maximum(0, np.dot(W2, H1) + b2)
out = np.dot(W3, H2) + b3
更多关于Dropout参见Dropout Training as Adaptive Regularization
分类与回归
回归问题:输出连续,常用来预测真实的值,例如房价。对于这样的任务,常用L2平方标准化作为损失函数。然而L2损失更加难以优化并且更加脆弱。在面对一个回归问题时候,判断是否绝对无法量化输出为多个空间,如果不是,就用分类方法。且L2损失函数的网络中并不适合用Dropout.
分类问题:输出离散。对于分类问题,大小合适即可,不必那么精确,且分类问题常用sorfmax损失,具体相关公式如下
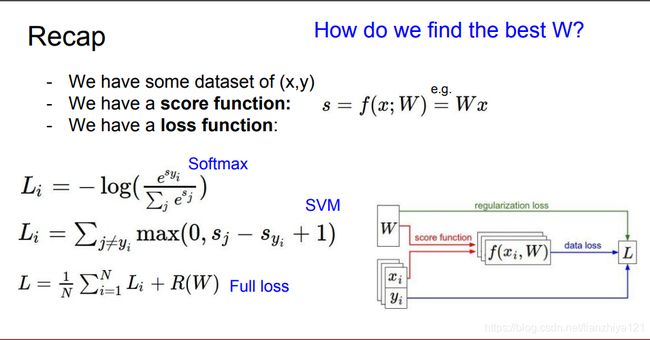
总结
-
推荐的处理过程是使得数据有零均值,且归一化每一个特征值范围在[-1,1]之间。
-
通过带有标准差的高斯分布初始化权重,n是输入的个数,w = np.random.randn(n) * sqrt(2.0/n)
-如果 使用L2正则化加使用Dropout(翻版) -
使用batch normalization ,如果无法满足条件,再使用其他技术
-
每种类型任务最常见的损失函数介绍
