超详细!!!匈牙利算法流程以及Python程序实现!!!通俗易懂
前不久在无人机检测跟踪的项目中用到了多目标跟踪算法(该项目后续会发贴介绍),其中需要涉及多个目标在两帧之间的匹配问题,最初使用的是最简单的距离最小化原则进行帧间多目标的匹配。后来通过实习和查阅论文等渠道了解到了多目标跟踪领域经典的Sort和DeepSort算法,其中都使用到了匈牙利算法解决匹配问题,因此开此贴记录一下算法的学习过程。
指派问题概述
首先,对匈牙利算法解决的问题进行概述:实际中,会遇到这样的问题,有n项不同的任务,需要n个人分别完成其中的1项,每个人完成任务的时间不一样。于是就有一个问题,如何分配任务使得花费时间最少。
通俗来讲,就是n*n矩阵中,选取n个元素,每行每列各有1个元素,使得和最小。
如下表所示
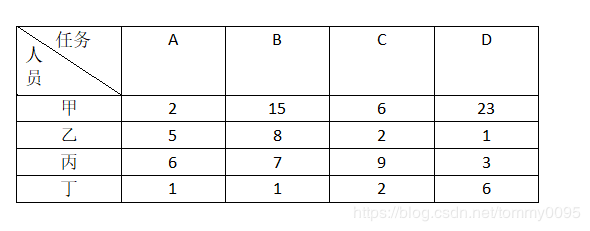
上表可以抽象成一个矩阵,如果是如上表所示的求和最小问题,那么这个矩阵就叫做花费矩阵(Cost Matrix);如果要求的问题是使之和最大化,那么这个矩阵就叫做利益矩阵(Profit Matrix)。
匈牙利算法流程
算法流程
匈牙利算法有多种实现方式,比如基于图论的方式等,本文主要使用矩阵变换来实现,这种方式你甚至可以在纸上写写画画,而且理解起来比较简单。

本文算法流程如上图所示,首先进行列规约,即每行减去此行最小元素,每一列减去该列最小元素,规约后每行每列中必有0元素出现。接下来进行试指派,也就是划最少的线覆盖矩阵中全部的0元素,如果试指派的独立0元素数等于方阵维度则算法结束,如果不等于则需要对矩阵进行调整,重复试指派和调整步骤直到满足算法结束条件。
以上是我简要描述的算法流程,值得一提的是,用矩阵变换求解的匈牙利算法也有多种实现,主要不同就在于试指派和调整矩阵这块,但万变不离其宗都是为了用最少的线覆盖矩阵中全部的零元素。咱们废话少说,来看一个例子。

程序实现
完整代码(带测试用例)
'''
@Date: 2020/2/23
@Author:ZhuJunHui
@Brief: Hungarian Algorithm using Python and NumPy
'''
import numpy as np
import collections
import time
class Hungarian():
"""
"""
def __init__(self, input_matrix=None, is_profit_matrix=False):
"""
输入为一个二维嵌套列表
is_profit_matrix=False代表输入是消费矩阵(需要使消费最小化),反之则为利益矩阵(需要使利益最大化)
"""
if input_matrix is not None:
# 保存输入
my_matrix = np.array(input_matrix)
self._input_matrix = np.array(input_matrix)
self._maxColumn = my_matrix.shape[1]
self._maxRow = my_matrix.shape[0]
# 本算法必须作用于方阵,如果不为方阵则填充0变为方阵
matrix_size = max(self._maxColumn, self._maxRow)
pad_columns = matrix_size - self._maxRow
pad_rows = matrix_size - self._maxColumn
my_matrix = np.pad(my_matrix, ((0,pad_columns),(0,pad_rows)), 'constant', constant_values=(0))
# 如果需要,则转化为消费矩阵
if is_profit_matrix:
my_matrix = self.make_cost_matrix(my_matrix)
self._cost_matrix = my_matrix
self._size = len(my_matrix)
self._shape = my_matrix.shape
# 存放算法结果
self._results = []
self._totalPotential = 0
else:
self._cost_matrix = None
def make_cost_matrix(self,profit_matrix):
'''利益矩阵转化为消费矩阵,输出为numpy矩阵'''
# 消费矩阵 = 利益矩阵最大值组成的矩阵 - 利益矩阵
matrix_shape = profit_matrix.shape
offset_matrix = np.ones(matrix_shape, dtype=int) * profit_matrix.max()
cost_matrix = offset_matrix - profit_matrix
return cost_matrix
def get_results(self):
"""获取算法结果"""
return self._results
def calculate(self):
"""
实施匈牙利算法的函数
"""
result_matrix = self._cost_matrix.copy()
# 步骤 1: 矩阵每一行减去本行的最小值
for index, row in enumerate(result_matrix):
result_matrix[index] -= row.min()
# 步骤 2: 矩阵每一列减去本行的最小值
for index, column in enumerate(result_matrix.T):
result_matrix[:, index] -= column.min()
#print('步骤2结果 ',result_matrix)
# 步骤 3: 使用最少数量的划线覆盖矩阵中所有的0元素
# 如果划线总数不等于矩阵的维度需要进行矩阵调整并重复循环此步骤
total_covered = 0
while total_covered < self._size:
time.sleep(1)
#print("---------------------------------------")
#print('total_covered: ',total_covered)
#print('result_matrix:',result_matrix)
# 使用最少数量的划线覆盖矩阵中所有的0元素同时记录划线数量
cover_zeros = CoverZeros(result_matrix)
single_zero_pos_list = cover_zeros.calculate()
covered_rows = cover_zeros.get_covered_rows()
covered_columns = cover_zeros.get_covered_columns()
total_covered = len(covered_rows) + len(covered_columns)
# 如果划线总数不等于矩阵的维度需要进行矩阵调整(需要使用未覆盖处的最小元素)
if total_covered < self._size:
result_matrix = self._adjust_matrix_by_min_uncovered_num(result_matrix, covered_rows, covered_columns)
#元组形式结果对存放到列表
self._results = single_zero_pos_list
# 计算总期望结果
value = 0
for row, column in single_zero_pos_list:
value += self._input_matrix[row, column]
self._totalPotential = value
def get_total_potential(self):
return self._totalPotential
def _adjust_matrix_by_min_uncovered_num(self, result_matrix, covered_rows, covered_columns):
"""计算未被覆盖元素中的最小值(m),未被覆盖元素减去最小值m,行列划线交叉处加上最小值m"""
adjusted_matrix = result_matrix
# 计算未被覆盖元素中的最小值(m)
elements = []
for row_index, row in enumerate(result_matrix):
if row_index not in covered_rows:
for index, element in enumerate(row):
if index not in covered_columns:
elements.append(element)
min_uncovered_num = min(elements)
#print('min_uncovered_num:',min_uncovered_num)
#未被覆盖元素减去最小值m
for row_index, row in enumerate(result_matrix):
if row_index not in covered_rows:
for index, element in enumerate(row):
if index not in covered_columns:
adjusted_matrix[row_index,index] -= min_uncovered_num
#print('未被覆盖元素减去最小值m',adjusted_matrix)
#行列划线交叉处加上最小值m
for row_ in covered_rows:
for col_ in covered_columns:
#print((row_,col_))
adjusted_matrix[row_,col_] += min_uncovered_num
#print('行列划线交叉处加上最小值m',adjusted_matrix)
return adjusted_matrix
class CoverZeros():
"""
使用最少数量的划线覆盖矩阵中的所有零
输入为numpy方阵
"""
def __init__(self, matrix):
# 找到矩阵中零的位置(输出为同维度二值矩阵,0位置为true,非0位置为false)
self._zero_locations = (matrix == 0)
self._zero_locations_copy = self._zero_locations.copy()
self._shape = matrix.shape
# 存储划线盖住的行和列
self._covered_rows = []
self._covered_columns = []
def get_covered_rows(self):
"""返回覆盖行索引列表"""
return self._covered_rows
def get_covered_columns(self):
"""返回覆盖列索引列表"""
return self._covered_columns
def row_scan(self,marked_zeros):
'''扫描矩阵每一行,找到含0元素最少的行,对任意0元素标记(独立零元素),划去标记0元素(独立零元素)所在行和列存在的0元素'''
min_row_zero_nums = [9999999,-1]
for index, row in enumerate(self._zero_locations_copy):#index为行号
row_zero_nums = collections.Counter(row)[True]
if row_zero_nums < min_row_zero_nums[0] and row_zero_nums!=0:
#找最少0元素的行
min_row_zero_nums = [row_zero_nums,index]
#最少0元素的行
row_min = self._zero_locations_copy[min_row_zero_nums[1],:]
#找到此行中任意一个0元素的索引位置即可
row_indices, = np.where(row_min)
#标记该0元素
#print('row_min',row_min)
marked_zeros.append((min_row_zero_nums[1],row_indices[0]))
#划去该0元素所在行和列存在的0元素
#因为被覆盖,所以把二值矩阵_zero_locations中相应的行列全部置为false
self._zero_locations_copy[:,row_indices[0]] = np.array([False for _ in range(self._shape[0])])
self._zero_locations_copy[min_row_zero_nums[1],:] = np.array([False for _ in range(self._shape[0])])
def calculate(self):
'''进行计算'''
#储存勾选的行和列
ticked_row = []
ticked_col = []
marked_zeros = []
#1、试指派并标记独立零元素
while True:
#print('_zero_locations_copy',self._zero_locations_copy)
#循环直到所有零元素被处理(_zero_locations中没有true)
if True not in self._zero_locations_copy:
break
self.row_scan(marked_zeros)
#2、无被标记0(独立零元素)的行打勾
independent_zero_row_list = [pos[0] for pos in marked_zeros]
ticked_row = list(set(range(self._shape[0])) - set(independent_zero_row_list))
#重复3,4直到不能再打勾
TICK_FLAG = True
while TICK_FLAG:
#print('ticked_row:',ticked_row,' ticked_col:',ticked_col)
TICK_FLAG = False
#3、对打勾的行中所含0元素的列打勾
for row in ticked_row:
#找到此行
row_array = self._zero_locations[row,:]
#找到此行中0元素的索引位置
for i in range(len(row_array)):
if row_array[i] == True and i not in ticked_col:
ticked_col.append(i)
TICK_FLAG = True
#4、对打勾的列中所含独立0元素的行打勾
for row,col in marked_zeros:
if col in ticked_col and row not in ticked_row:
ticked_row.append(row)
FLAG = True
#对打勾的列和没有打勾的行画画线
self._covered_rows = list(set(range(self._shape[0])) - set(ticked_row))
self._covered_columns = ticked_col
return marked_zeros
if __name__ == '__main__':
#以下为3个测试用例
cost_matrix = [
[4, 2, 8],
[4, 3, 7],
[3, 1, 6]]
hungarian = Hungarian(cost_matrix)
print('calculating...')
hungarian.calculate()
print("Expected value:\t\t12")
print("Calculated value:\t", hungarian.get_total_potential()) # = 12
print("Expected results:\n\t[(0, 1), (1, 0), (2, 2)]")
print("Results:\n\t", hungarian.get_results())
print("-" * 80)
profit_matrix = [
[62, 75, 80, 93, 95, 97],
[75, 80, 82, 85, 71, 97],
[80, 75, 81, 98, 90, 97],
[78, 82, 84, 80, 50, 98],
[90, 85, 85, 80, 85, 99],
[65, 75, 80, 75, 68, 96]]
hungarian = Hungarian(profit_matrix, is_profit_matrix=True)
hungarian.calculate()
print("Expected value:\t\t543")
print("Calculated value:\t", hungarian.get_total_potential()) # = 543
print("Expected results:\n\t[(0, 4), (2, 3), (5, 5), (4, 0), (1, 1), (3, 2)]")
print("Results:\n\t", hungarian.get_results())
print("-" * 80)
profit_matrix = [
[62, 75, 80, 93, 0, 97],
[75, 0, 82, 85, 71, 97],
[80, 75, 81, 0, 90, 97],
[78, 82, 0, 80, 50, 98],
[0, 85, 85, 80, 85, 99],
[65, 75, 80, 75, 68, 0]]
hungarian = Hungarian(profit_matrix, is_profit_matrix=True)
hungarian.calculate()
print("Expected value:\t\t523")
print("Calculated value:\t", hungarian.get_total_potential()) # = 523
print("Expected results:\n\t[(0, 3), (2, 4), (3, 0), (5, 2), (1, 5), (4, 1)]")
print("Results:\n\t", hungarian.get_results())
print("-" * 80)
总结
如开篇所言,匈牙利算法具有多种实现方式,可见该算法多么优秀,本文的实现方式不一定是最优的,但相对而言比较通俗易懂。值得一提的是,在python中使用该算法直接调用一个函数就可解决(如下代码段)。
from scipy.optimize import linear_sum_assignment
cost =np.array([[4,1,3],[2,0,5],[3,2,2]])
row_ind,col_ind=linear_sum_assignment(cost)
print(row_ind)#开销矩阵对应的行索引
print(col_ind)#对应行索引的最优指派的列索引
print(cost[row_ind,col_ind])#提取每个行索引的最优指派列索引所在的元素,形成数组
print(cost[row_ind,col_ind].sum())#数组求和 输出:[0 1 2][1 0 2] [1 2 2] 5
后续我还会发帖介绍此算法在多目标跟踪算法中的使用以及多目标跟踪算法本身,这是我的第一篇博客,如有错误欢迎指正,转载请告知,作图不易希望大家喜欢。