MATLAB数学建模：智能优化算法-神经网络算法

智能优化算法: 神经网络算法

人工神经网络的构筑是受生物神经网络的运作而启发的. 人工神经网络通常通过一个基于数学统计学类型的学习方法从而得以优化, 因此人工神经网络也可被看作是数学统计学方法的一种应用.

通过统计学的标准数学方法, 我们可以得到大量的, 可用函数表达的局部结构空间, 在人工智能学的人工感知领域, 通过数学统计学的应用可以解决人工感知方面的决定问题, 这种方法比起常规的逻辑学推理演算具有更大的优势.

1. 基本原理

人工神经网络模型的区别主要在 神经网络连接的拓扑结构, 神经元的特征和学习规模等等. 根据神经元连接的拓扑结构的区别, 我们大致可将神经网络模型分为以下两种:

1. 前向网络

   在前向网络中, 每个神经元只接受前一级的输入并输出到后一级, 在神经网络中没有反馈. 它的拓扑结构可用一个有向无环路图表示. 这种网络所实现的是信号从输入空间到输出空间的变换, 其信息处理能力在于简单非线性函数的有限次复合.

   最简单的前向网络结构是 两层前向网络结构, 该网络只有输入层和输出层. 一般地, 含有一个输入层, 一个输出层和多个中间层的前向神经网络被称为 多层前向网络结构.

2. 反馈网络
   另一种神经网络模型类型被称为 反馈网络, 这类网络的神经元之间存在反馈, 其拓扑结构可以用一个无向的完备图表示. 其信息处理能力源于状态的变换, 可以用动力系统理论处理. 系统的稳定性和联想记忆功能有密切关系.

2. 程序设计

MATLAB 的神经网络工具箱中预置了多种神经网络函数, 包括:

1. 感知器
2. 线性网络
3. BP神经网络
4. 径向基函数网络
5. 竞争型神经网络
6. 自组织网络和学习向量量化网络
7. 反馈网络

下面, 对重要的神经网络工具箱函数进行介绍:

2.1 通用神经网络工具箱函数

下面介绍数个通用函数的基本功能和用法:

2.1.1 神经网络初始化函数 init

利用神经网络初始化函数 init, 我们可对一个现存的神经网络参数进行初始化, 修正这个神经网络的权值, 偏值等参数.
该函数调用格式为:

net = init(NET)

其中, NET 是尚未初始化的神经网络, net是经过初始化的神经网络.

2.1.2 单层神经网络初始化函数 initlay()

利用函数 initlay(), 我们可对单层神经网络进行初始化, 修正其权值和偏值. 该函数调用格式为:

net = initlay(NET)

其中, NET 是尚未初始化的神经网络, net是经过初始化的神经网络.

2.1.3 神经网络单层权值和偏值初始化函数 initwb()

该函数可对神经网络某一层的权值和偏值进行初始化修正. 调用格式为:

net = initwb(NET,i)

其中, NET 是尚未初始化的神经网络, net是第 $i$ 层经过初始化的神经网络, i 为需要进行权值和偏值修正的目标层数.

2.1.4 神经网络训练函数 train()

该通用函数的作用是训练神经网络: 不断重复地将一组输入向量应用于某一个神经网络, 实时更新它的权值和偏值, 当神经网络训练达到所设定的最大学习步长, 最小误差梯度, 误差目标等条件后停止训练. 函数调用格式如下:

[net,tr,Y,E] = train(NET,X,T,Xi,Ai)

其中:

1. NET - 受训神经网络
2. X - 神经网络输入
3. T - 训练神经网络的目标输出, 默认值为0
4. Xi - 初始输入延时, 默认值为0
5. Ai - 初始层延时
6. net - 完成训练的神经网络
7. tr - 神经网络训练的步长
8. Y - 神经网络的输出
9. E - 神经网络训练误差

在调用该函数之前, 必须先设定 训练函数, 训练步长, 训练目标误差 等参数. 若没有设定, train 函数将调用默认的训练参数对神经网络进行训练.

2.1.5 神经网络仿真函数 sim

该函数的作用是在完成神经网络训练后检测已完成训练的神经网络的性能.其调用格式如下:

[Y,Xf,Af,E] = sim[net,X,Xi,Ai,T]

其中:

1. net - 受训神经网络
2. X - 神经网络输入
3. Xi - 初始输入延时
4. Ai - 初始层延时
5. T - 训练神经网络的目标输出
6. Y - 神经网络输出
7. Xf - 最终输入延时
8. Af - 最终层延时
9. E - 神经网络训练误差

2.1.6 神经网络输入的和函数netsum

该函数通过神经网络的某一层的加权输入和偏值相加,作为该层的输入. 调用格式如下:

N = netsum({Z1,Z2,...,Zn},FP)

其中, $Zn$ 为 $S\ast Q$ 维矩阵.

[例]

使用 netsum 函数将两个权值和一个偏值相加:

z1 = [1 2 4;3 4 1];
z2 = [-1 2 2;-5 6 1];
b = [0;-1];
n = netsum({z1,z2,concur(b,3)})

即得到神经网络输入:

n =

     0     4     6
    -3     9     1

>> 

2.1.7 权值点积函数 dotprod

dotprod令神经网络的输入向量和权值点积, 可得加权输入. 该函数调用格式如下:

Z = dotprod(W,P,FP)

其中, $W$ 为权值矩阵, $P$ 为输入向量, $FP$ 为可省略的功能参数, $Z$ 为权值矩阵和输入向量的点积.

[例]

使用 dotprod 函数求得一个点积:

W = rand(4,3);
P = rand(3,1);
Z = dotprod(W,P)

即得到点积: (输入变量均为随机生成,实机操作输出结果不定)

Z =

    1.1244
    0.7101
    2.3575
    0.1860

>> 

2.1.8 神经网络输入的积函数netprod

netprod 函数将神经网络某一层甲醛输入和偏值相乘的结果作为该层的输入. 其调用格式为:

N = netprod({Z1,Z2,...,Zn})

其中, $Zn$ 为 $Z\ast Q$ 维矩阵.

[例]

使用 netprod 函数求得神经网络输入的积:

Z1 = [1,2,4;3,4,1];
Z2 = [-1 2 2;-5 -6 1];
B = [0;-1];
Z = {Z1,Z2,concur(B,3)};
N = netprod(Z)

即得到:

N =

     0     0     0
    15    24    -1

>> 

2.2 感知器

在 MATLAB 神经网络工具箱中有大量和感知器相关的函数. 下面对它们进行简介:

2.2.1 绘制样本点函数 plotpv

plotpv 函数可在坐标图中绘出样本点及其类别, 不同类别使用不同的符号. 调用格式如下:

plotpv(P,T)

其中, $P$ 为 $n$ 个二维或三维的样本矩阵, $T$ 表示各个样本点的类别.

2.2.2 绘制分类线函数 plotpc

该函数功能是在已知的样本分类图中绘制出样本分类线. 调用格式如下:

plotpc(W,B)

其中, $W$ 和 $B$ 分别是神经网络的权矩阵和偏差向量.

2.2.3 感知器学习函数 learnp

learnp 利用感知器学习规则训练单层神经网络. 感知器学习规则是通过调整神经网络的权值和偏值, 使得感受器平均误差和最小, 以便对输入向量进行正确的分类. 该函数的调用格式为:

[dW,LS] = learnp(P,T,E)

其中, $P$ 为输入向量矩阵, $T$ 为目标向量, $E$ 为误差向量. $dW$, $LS$ 分别为权值和偏值变化矩阵.

2.2.4 平均绝对误差性能函数 mae

该函数用于输出神经网络的平均误差. 调用格式为:

perf = mae(E,Y,X,FP)

其中, $E$ 为感知器输出误差矩阵, $Y$ 表示感知器的输出向量, $X$ 表示感知器的权值和偏值向量.

2.3 线性神经网络函数

MATLAB 的神经网络工具箱中预置了多种线性神经网络函数. 下面对一些线性神经网络函数进行简介.

2.3.1 误差平方和性能函数sse

线性神经网络的学习规则是调整其权值和偏值, 使其误差的 平方和 最小. 误差平方和性能函数的调用格式为:

perf = sse(net,t,y,ew)

其中, net 为所建立的神经网络, $t$ 为目标向量, $y$ 为网络输出向量, ew为权值误差, perf 为误差平方和.

2.3.2 计算线性层最大稳定学习速率函数 maxlinlr

该函数用于计算使用 Widrow-Hoff 准则所训练出的线性神经网络的最大稳定学习速率. 调用格式如下;

lr = maxlinlr(P,'bias')

其中, $P$ 为输入向量, bias 为神经网络偏值, lr 为学习速率.

[注]

一般而言, 学习速率越高, 神经网络所需的训练时间越短, 网络收敛速度越快, 学习效果越不稳定.

2.3.3 网络学习函数 learnwh

该函数称为 最小方差准则学习函数. 调用格式如下:

[dW, LS] = learnwh(W,P,Z,N,A,T,E,gW,gA,D,LP,LS)

其中:

1. W - 权值矩阵
2. P - 输入向量
3. Z - 权值输入向量
4. N - 神经网络输入向量
5. A - 神经网络输出向量
6. T - 目标向量
7. E - 误差向量
8. gW - 权值梯度向量
9. gA - 输出梯度向量
10. D - 神经元间隔
11. LP - 学习函数
12. LS - 学习状态

[注]

dW 和 LS 分别为神经网络的权值和偏值的调整值.

[例]

利用 learnwh 函数获取神经网络权值调整值:

p = rand(2,1);
e = rand(3,1);
lp.lr = 0.5;
dW = learnwh([],p,[],[],[],[],e,[],[],[],lp,[])

代码运行后得到的权值调整值如下:

dW =

    0.0110    0.0519
    0.0338    0.1599
    0.0182    0.0862

>> 

2.3.4 线性神经网络设计函数 newlind

该函数可设计出可以直接使用的线性神经网络. 调用格式如下;

net = newlind(P,T,Pi)

其中, $P$ 为输入向量, $T$ 为目标向量, Pi 为神经元起始状态参数, net 为建立的线性神经网络.

[例]

利用 newlind 函数建立一个线性神经网络并测试其性能.

[解]

编写代码如下:

P = {1 2 1 3 3 2};
Pi = {1 3};
T = {5.0 6.1 4.0 6.0 6.9 8.0};
net = newlind(P,T,Pi);
Y = sim(net,P,Pi)

代码运行结果如下:

Y =

  1×6 cell array

    {[4.9824]}    {[6.0851]}    {[4.0189]}    {[6.0054]}    {[6.8959]}    {[8.0122]}

>> 

注:

在使用 newlind 函数时, 参数 Pi 可以省略.

2.4 BP神经网络函数

下面简介一些常用的BP神经网络函数及其基本功能:

2.4.1 均方误差性能函数 mse

BP神经网络的学习规则是通过不断调整神经网络的权值和偏值, 从而使得网络输出的均方误差和最小. mse 函数调用格式为:

perf = mse(net,t,y,ew)

其中, net 为所建立的神经网络, $t$ 为目标向量, $y$ 为网络输出向量, ew为所有权值和偏值向量, perf 为均方误差.

2.4.2 误差平方和函数 sumsqr

sumsqr 函数的作用是计算输入向量平方和. 调用格式为:

[s,n] = sumsqr(x)

其中, $x$ 为输入向量, $s$ 为有限值的平方和, $n$ 为有限值的个数.

2.4.3 计算误差曲面函数 errsurf

该函数的功能是计算单输入神经元输出误差平方和. 调用格式为:

errsurf(P,T,WV,BV,F)

其中, $P$ 为输入向量, $T$ 为目标向量, $WV$ 为权值矩阵, $BV$ 为偏值矩阵, $F$ 为传输函数.

2.4.4 误差曲面图绘制函数 plotes

该函数的作用是绘制误差曲面图. 调用格式为:

plotes(WV,BV,ES,V)

其中, $WV$ 为权值矩阵, $BV$ 为偏值矩阵, $ES$ 为误差曲面, $V$ 为期望的视角.

[例]

可使用以下代码绘制误差曲面图:

p = [3 2];
t = [0.4 0.8];
wv = -4:0.4:4;
bv = wv;
ES = errsurf(p,t,wv,bv,'logsig');
plotes(wv,bv,ES,[60 30])

所得误差曲面图如下图所示:

2.4.5 误差曲面图权值偏值位置绘制函数 plotep

该函数的作用是在由函数 plotes 所生成的误差曲面图上绘制出单输入网络权值 $W$ 和偏差 $B$ 所对应的误差 $e$ 的位置. 调用格式为:

H = plotep(W,B,e)

其中, $W$ 为偏值矩阵, $B$ 为偏值向量, $e$ 为输出误差.

[例]

p = [3 2];
t = [0.4 0.8];
wv = -4:0.4:4;
bv = wv;
ES = errsurf(p,t,wv,bv,'logsig');
plotes(wv,bv,ES,[60 30])
W = -3;
B = 1;
E = sumsqr(t-sumuff(p,W,B,'logsig'));
plotep(W,B,e)

运行后即得到权值和偏值在误差曲面上的位置.
(本飞舞的MATLAB上连sumuff函数都没有，，，哭哭，，，)

2.5 径向基神经网络函数

下面简介一些常用的径向基神经网络函数及其功能:

2.5.1 向量距离计算函数 dist

大多数神经网络的输入可通过表达式: $Y=W\ast X+B$ 得到: $W,B$ 分别为神经网络的权向量和偏值向量. 但有些神经元的输入可由函数 dist 计算. 该函数是一个欧式距离权值函数, 它对输入加权以得到被加权的输入. 函数的调用格式如下:

Z = dist(W,P,FP)
D = dist(pos)

其中, $W$ 为神经网络的权值矩阵, $P$ 为输入向量, $Z,D$ 均为输出距离矩阵. pos 为神经元位置参数矩阵.

[例]

定义一个两层神经网络, 每层神经网络包含三个神经元. 使用函数 dist 计算该神经网络所有神经元之间的距离:

pos = rand(2,3);
D = dist(pos)

运行所得结果:

D =

         0    0.6479    1.0356
    0.6479         0    0.7349
    1.0356    0.7349         0

>> 

2.5.2 径向基传输函数 radbas

该函数作用于径向基神经网络输入矩阵的每一个输入量. 调用格式为:

A = radbas(N)

其中, $N$ 为神经网络的输入矩阵, $A$ 为函数的输出矩阵.

2.5.3 径向基神经网络建立函数 newrb

newrb 可用于重新创建一个径向基神经网络. 该函数调用格式如下:

net = newrb(P,T,goal,spread,MN,DF)

其中, $P$ 为输入向量, $T$ 为目标向量. goal 为均方误差, spread 为径向基函数的扩展速度. $MN$ 为神经元的最大数目, $DF$ 为两次显示之间所添加的神经元数目. $net$ 为生成的径向基神经网络.

[注]

利用 newrb 函数建立的径向基神经网络, 也可不经过训练而直接使用.

[例]

使用 newrb 建立径向基神经网络, 并实现函数逼近.

[解]

编写的代码如下:

clc;clear all;
X = 0:0.1:2;               %神经网络输入值
T = cos(X*pi);             %神经网络目标值

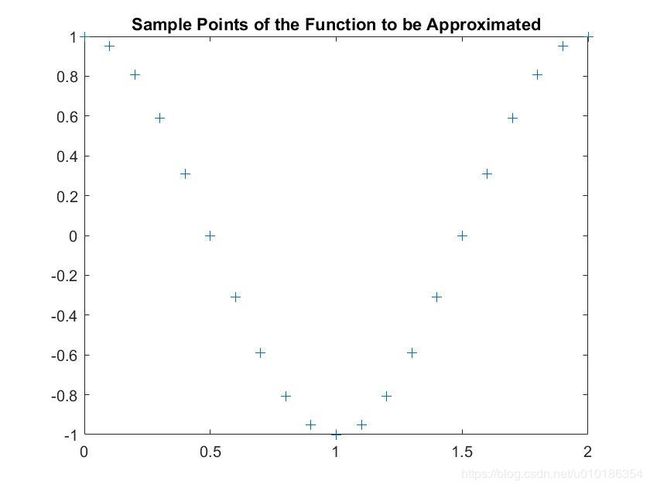
%% 绘制该函数上的采样点
figure(1)
plot(X,T,'+');
title('Sample Points of the Function to be Approximated');
xlabel = ('Input Values');
ylabel = ('Target Values');

%% 建立神经网络并进行仿真
n = -4:0.1:4;
a1 = radbas(n)
a2 = radbas(n-1.5);
a3 = radbas(n+2);
a = a1 + 1*a2 + 0.5*a3;
figure(2);
plot(n,a1,n,a2,n,a3,n,a,'x');
title('Weighted Sum of Radial Basis Networks');
xlabel = ('Input Values');
ylabel = ('Target Values');

% 径向基函数神经网络隐含层中每个神经元的权重和阈值
% 都指定了相应的径向基函数的位置和宽度. 
%每一个线性输出神经元都由这些径向基函数的加权和组成.
 
net = newrb(X,T,0.03,2);   %设定平方和误差参数为0.03
X1 = 0:0.01:2;
y = sim(net,X1);
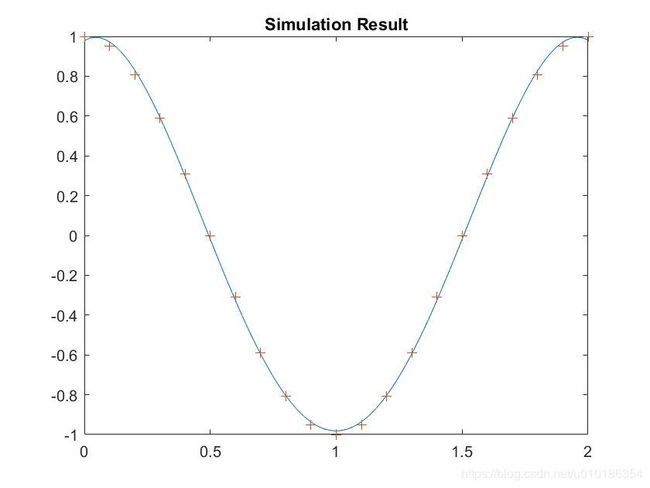
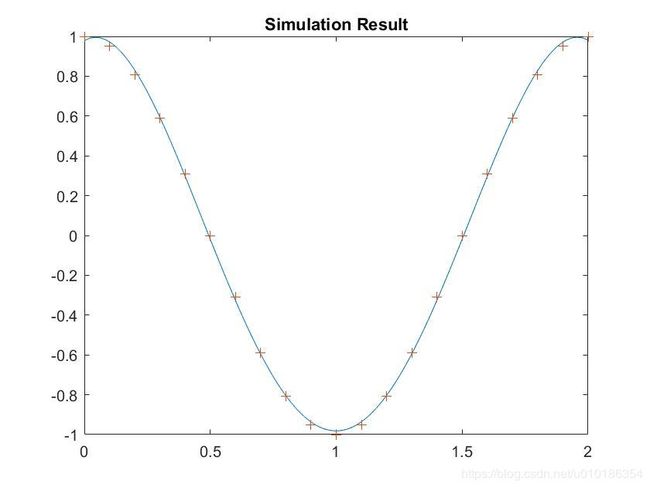
figure(3);
plot(X1,y,X,T,'+');
title('Simulation Result');
xlabel = ('Input Values');
ylabel = ('Network & Target Output');
 

程序运行后得到:

待逼近的函数样本点图形:

建立的径向基传递函数加权和:

建立的径向基神经网络仿真结果:

[注]

因为径向基神经网络需要更多的隐含层神经元完成训练, 故径向基神经网络不可用于取代其他前馈网络.

2.5.4 严格径向基神经网络建立函数 newrbe

建立严格径向基神经网络的函数为 newrbe, 调用格式如下:

net = newrbe(P,T,speed)

其中, $P$ 为输入向量 , $T$ 为目标向量, speed 为径向基函数的扩展速度, 默认值为 $1$, net 为生成的神经网络.

[注]

利用 newrbe 生成的径向基神经网络可不经过训练而直接使用:

[例]

在MATLAB 中利用以下代码建立一个径向基神经网络:

>> P = [1 2 3 4 5 6 7];
>> T = [8.1 0.8 9.3 6.4 3.6 4.1 1.4];
>> net = newrbe(P,T);
>> P = 2;
>> Y = sim(net, P)

代码执行结果:

Y =

    0.8000

>> 

可见, 所建立的,未经训练的径向基神经网络也正确地预测出了输出值.

2.5.5 广义回归径向基神经网络函数 newgrnn

广义回归径向基网络 GRNN 训练速度快, 非线性映射能力强, 常用于函数的逼近. 其调用格式为:

net = newgrnn(P,T,spread)

其中, $P$ 为输入向量, $T$ 为目标向量, spread 为径向基函数的扩展速度, 默认值为 $1$, net 为所生成的神经网络.

[注]

一般而言, spread 取值越小神经网络逼近效果越好, 但逼近过程越不平滑.

2.5.6 数据索引向量-向量组变换函数 ind2vec

函数 ind2vec 的作用是对向量进行变换, 将数据索引向量变换为向量组. 调用格式为:

vec = ind2vec(ind)

其中, ind 是 $n$ 维数据索引行向量, vec 为 $m$ 行 $n$ 列的稀疏矩阵.

2.5.7 向量组-数据索引向量变换函数 vec2ind

函数 vec2ind 的作用是对向量进行变换, 将向量组变换为数据索引向量, 可视为ind2vec 的逆操作函数. 其调用格式为:

ind = vec2ind(vec)

其中, ind 是 $n$ 维数据索引行向量, vec 为 $m$ 行 $n$ 列的稀疏矩阵.

2.5.8 概率径向基函数 newpnn

该函数命令用于建立概率径向基神经网络, 具有训练速度快, 结构简单的特点, 适合解决模式分类问题. 函数调用格式如下:

net = newpnn(P,T,spread)

其中, $P$ 为输入向量, $T$ 为目标向量, spread 为径向基函数的扩展速度, net 为所生成的神经网络.

[注]

该函数生成的神经网络和严格径向基神经网络建立函数 newrbe 所建立的神经网络一样, 可以不经过训练而直接使用.

[例]

建立一个概率径向基神经网络并进行仿真:

P = [1 2 3 4 5 6 7 8];
Tc = [1 1 4 5 1 4 1 9];
T = ind2vec(Tc)     %将类别向量转换为可使用的目标向量组
net = newpnn(P,T);
Y = sim(net,P)
Yc = vec2ind(Y)     %将仿真结果转换为类别向量

所得结果如下:

T =

   (1,1)        1
   (1,2)        1
   (4,3)        1
   (5,4)        1
   (1,5)        1
   (4,6)        1
   (1,7)        1
   (9,8)        1


Y =

     1     1     0     0     1     0     1     0
     0     0     0     0     0     0     0     0
     0     0     0     0     0     0     0     0
     0     0     1     0     0     1     0     0
     0     0     0     1     0     0     0     0
     0     0     0     0     0     0     0     0
     0     0     0     0     0     0     0     0
     0     0     0     0     0     0     0     0
     0     0     0     0     0     0     0     1


Yc =

     1     1     4     5     1     4     1     9

>> 

2.6 自组织神经网络函数

下面简介一些常用的自组织神经网络函数及其功能:

2.6.1 竞争神经网络建立函数 newc

函数newc 可用于建立一个竞争型神经网络. 其调用格式为:

net = newc(P,S)

其中, $P$ 为决定输入列向量最大最小值取值范围的矩阵, $S$ 表示神经网络中神经元的个数, net 表示建立的竞争神经网络.

[例]

建立并训练一个竞争型神经网络:

P = [1 9 1 9 ;1 1 4 5];
net = newc([-1 1;-1 1],3);
net = train(net,P);
y = sim(net,P);
yc = vec2ind(y)

所得结果:

Y =

     1     1     0     0     1     0     1     0
     0     0     0     0     0     0     0     0
     0     0     0     0     0     0     0     0
     0     0     1     0     0     1     0     0
     0     0     0     1     0     0     0     0
     0     0     0     0     0     0     0     0
     0     0     0     0     0     0     0     0
     0     0     0     0     0     0     0     0
     0     0     0     0     0     0     0     1


Yc =

     1     1     4     5     1     4     1     9

>> jingzhengxingshenjingwanglnewc

yc =

     1     2     3     2

>> 

竞争型神经网络训练如下图所示:

2.6.2 竞争传输函数 compet

compet 函数可对竞争神经网络的输入进行转换, 使得网络中有最大输入值的神经元的输出为 $1$, 且其余神经元的输出为 $0$. 调用格式如下:

A = compet(N)

其中, $A$ 为输出向量矩阵, $N$ 为输入向量.

2.6.3 一定类别的样本向量生成函数 nngenc

函数调用格式如下:

x = nngenc(bounds, clusters, points, std_dev)

其中, $x$ 是具有一定类别的样本向量, bounds 指类中心的范围, clusters 指类别数目, points 指每一类的样本点数目, std_dev 指每一类样本点的标准差.

[例]

%创建输入样本向量
bounds = [0,1;0,1];  %类中心的范围
clusters = 5;        %类的个数
points = 14;         %每个类的点数
std_dev = 0.05;      %每个样本点的标准差
x = nngenc(bounds, clusters, points, std_dev)

%%绘制输入样本的样本向量图
plot(x(1,:),x(2:,),'+'r);
title('Imput Vectors');
xlabel('x(1)');
ylabel('x(2)');

程序运行结果如下图所示:

(然而本飞舞的MATLAB上这个函数也没有，，，)

2.6.4 自组织网络权值向量绘制函数 plotsum

该函数的作用是在神经网络的每个神经元权向量对应坐标处画点, 并用实线连接起神经元权值点. 调用格式如下:

plotsum(pos)

其中, pos 是表示 $N$ 维坐标点的 $N\ast S$ 维矩阵.

2.6.5 Kohonen 权值学习规则函数 learnk

learnk 函数根据 Kohonen 准则计算神经网络的权值变化矩阵. 调用格式如下:

[dW,LS] = learnk(W,P,Z,N,A,T,E,gW,gA,D,LP,LS)

其中:

1. dW - 权值变化矩阵
2. LS - 新的学习状态
3. W - 权值矩阵
4. P - 输入向量
5. Z - 权值输入向量
6. N - 神经网络输入向量
7. T - 目标向量
8. E - 误差向量
9. gW - 性能参数梯度
10. gA - 性能参数的输出梯度
11. LP - 学习速率 (默认为0.01)
12. LS - 学习状态

2.6.6 Hebb 权值学习规则函数 learnh

learnh 函数的原理是 $\Delta \omega (i,j)=\eta \ast y(i)\ast x(j).$ 即第 $j$ 个输入和第 $i$ 个神经元之间的权值变化量神经元输入和输出的乘积成正比. 调用格式如下:

[dW,LS] = learnh(W,P,Z,N,A,T,E,gW,gA,D,LP,LS)

其中,函数各变量含义和 learnk 函数中的完全一致.

2.6.7 输入向量加权值计算函数 negdist

函数调用格式如下:

Z = negdist(W,P)

其中, $Z$ 为负向量距离矩阵, $W$ 为权值函数, $P$ 为输入矩阵.

中, `pos` 是表示 $N$ 维坐标点的 $N*S$ 维矩阵.

2.6.5 Kohonen 权值学习规则函数 learnk

learnk 函数根据 Kohonen 准则计算神经网络的权值变化矩阵. 调用格式如下:

[dW,LS] = learnk(W,P,Z,N,A,T,E,gW,gA,D,LP,LS)

其中:

1. dW - 权值变化矩阵
2. LS - 新的学习状态
3. W - 权值矩阵
4. P - 输入向量
5. Z - 权值输入向量
6. N - 神经网络输入向量
7. T - 目标向量
8. E - 误差向量
9. gW - 性能参数梯度
10. gA - 性能参数的输出梯度
11. LP - 学习速率 (默认为0.01)
12. LS - 学习状态

2.6.6 Hebb 权值学习规则函数 learnh

learnh 函数的原理是 $\Delta \omega (i,j)=\eta \ast y(i)\ast x(j).$ 即第 $j$ 个输入和第 $i$ 个神经元之间的权值变化量神经元输入和输出的乘积成正比. 调用格式如下:

[dW,LS] = learnh(W,P,Z,N,A,T,E,gW,gA,D,LP,LS)

其中,函数各变量含义和 learnk 函数中的完全一致.

2.6.7 输入向量加权值计算函数 negdist

函数调用格式如下:

Z = negdist(W,P)

其中, $Z$ 为负向量距离矩阵, $W$ 为权值函数, $P$ 为输入矩阵.

3. 常见应用

神经网络是由人工基本神经元相互连接, 模拟人脑神经处理信息方式解决问题的工具. 神经网络可以解决很多利用传统方法无法解决的问题.

3.1 BP神经网络

BP神经网络具有很强的 映射能力, 主要应用有: 模式识别分类, 函数逼近, 函数压缩 等.

[例]函数逼近:
设计一个 BP 神经网络, 逼近函数$$g(x)=1+sin(\frac{k\pi }{2x}).$$ 其中, 分别令 $k=2,3,6$ 进行仿真, 通过调节参数得出信号频率和隐含层节点之间, 隐含层节点与函数逼近能力之间的关系.

[解]
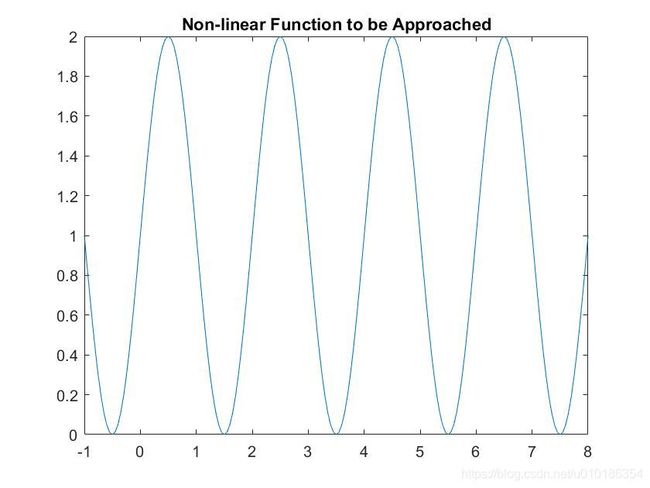
设频率参数 $k=2$, 绘制要毕竟的非线性函数的目标曲线:

k = 2;p = [-1:.05:8];
t = 1+sin(k*pi/2*p);
plot(p,t,'-');
title('Non-linear Function to be Approached');
xlabel = ('Time');
ylabl = ('Non-linear Function');

运行后得到目标曲线如下图所示:

使用 newff 函数建立BP神经网络:

n = 5;          %设定隐含层神经元数目为5
net = newff(minmax(p),[n,1],{'tansig','purelin'},'trainlm');
%选择隐含层和输出层神经元传递函数为 tansig 和 purelin,
%网络训练算法采用 Levenberg-Marquardt 算法 trainlm.
%对于初始神经网络, 可使用 sim() 函数观察网络输出
y1 = sim(net,p);
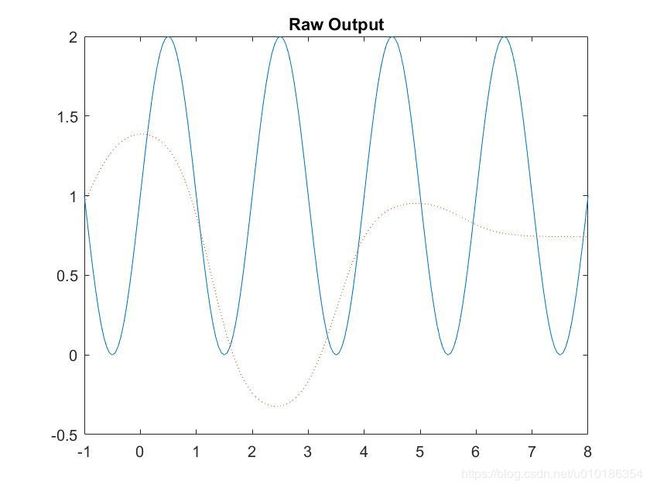
figure;
plot(p,t,'-',p,y1,':')
title('Raw Output');
xlabel('Time');
ylabel('Simulation Output----Original Function')

程序运行后所得到的神经网络输出曲线和原函数的对比图:

使用 newff 函数建立神经网络时权值和阈值的初始化是随机的, 故网络输出的结构很差, 达不到逼近函数的目的.
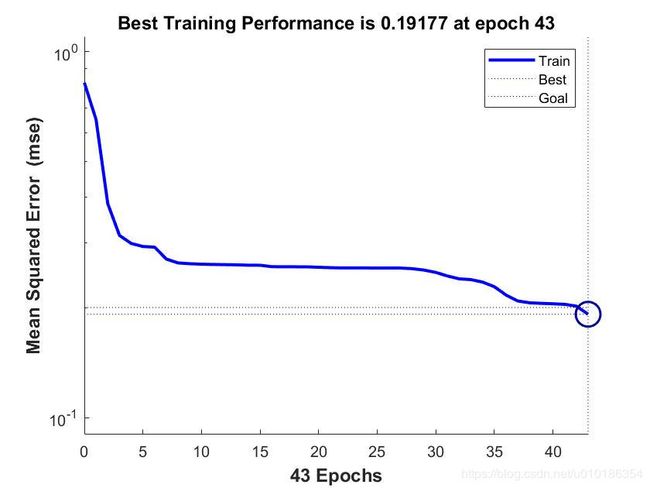
下面设置网络训练参数, 应用 train 函数对网络进行训练:

net = trainParam.epochs = 200;  %设定网络训练步长为200
net.trainParam.goal = 0.2;      %设定网络训练精度为0.2
net = train(net,p,t);           %开始执行网络训练

训练过程中的误差变化状态如下图所示:

下面对训练出的神经网络进行仿真:

y2 = sim(net,p);
figure;
plot(p,t,'-',p,y1,':',p,y2,'--')
title('Output of the Trained Neural Network');
xlabel('Time')ylabel('Simulation Output')

下图为训练所得的神经网络的输出结果:

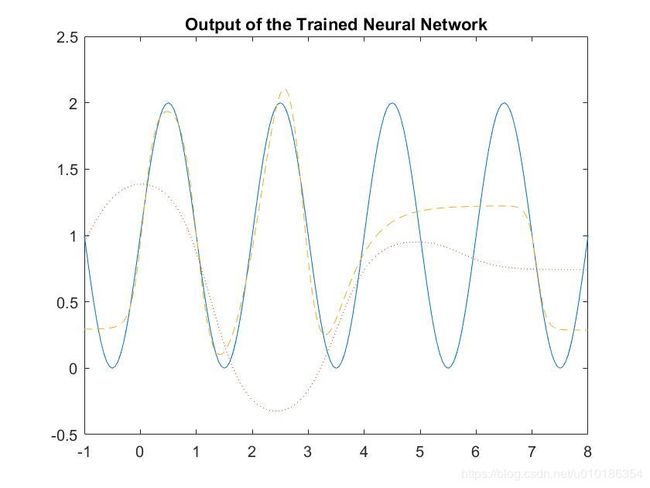
不难看出, 经过训练后的 BP 神经网络对非线性函数的逼近效果有显著提升.

实际上, 改变非线性函数的频率和 BP 神经网络隐含层神经元的数目, 也会对神经网络逼近函数的效果有一定影响. 一般而言, 隐含层神经元数目越多, BP 网络逼近非线性函数的能力越强.