Dropout Regularization（丢弃正则化）

Dropout Regularization（丢弃正则化）

        为了防止过拟合的问题，我们最常使用的手段就是L2正则化，即在代价函数后面加一个L2正则项。关于L2正则化，我前面的博客已经讲了很多次了，这里就不在赘述了。这篇博客主要介绍下dropout regularization（丢弃正则化），dropout正则化是Srivastava在2014年提出来的：Dropout: A Simple Way to Prevent Neural Networks from Over tting。Dropout的思想其实非常简单粗暴：对于网络的每一层，随机的丢弃一些单元。如下图所示（图片来自Srivastava的dropout论文）：

关于为什么dropout能够减轻过拟合，ng给出了两个比较直观的解释：

• 正是因为在每一层随机的丢弃了一些单元，所以相当于训练出来的网络要比正常的网络小的多，在一定程度上解释了避免过拟合的问题。
• 如下图所示的一个简单单层网络，因为每一个特征都有可能被丢弃，所以整个网络不会偏向于某一个特征（把某特征的权重的值赋的很大），会把每一个特征的权重都赋的很小，这就有点类似于L2正则化了，能够起到减轻过拟合的作用。
  

这个方法看起来有点疯狂，但是他确实是有效的。下面开始从技术实现方面来看下dropout正则项，这里最重要的一个参数就是 keep_prob k e e p _ p r o b ，称作保留概率（同样， 1−keep_prob 1 − k e e p _ p r o b 则为丢弃概率），比如某一层的 keep_prob=0.8 k e e p _ p r o b = 0.8 ，则意味着某一层随机的保留80%的神经单元（也即有20%的单元被丢弃）。通常实现dropout regularization的技术称为 inverted dropout，假设对于第三层，则inverted dropout的具体实现为：

1.  d3 = np.random.rand(a3.shape[0],a3.shape[1]) < keep_prob
2.  a3 = np.multiply(a3,d3)
3.  a3 = a3 / keep_prob
4.  z4 = np.dot(w4,a3) + b4

关于上面的步骤的说明一些说明：

第1步，新建一个大小和 a3 a 3 一样的概率矩阵，其实这一样代码，因为每次都是随机数，所以只能做到近似保留 keep_prob k e e p _ p r o b 这么多，比如， keep_prob=0.8 k e e p _ p r o b = 0.8 可能d3只有79%的1，也就意味着只有79%的单元被保留，但是如果隐藏层单元数量越多，越能够逼近80%。
第2步， a3 a 3 与 d3 d 3 点乘，即保留 keep_prob k e e p _ p r o b 的单元，剩下的 1−keep_prob 1 − k e e p _ p r o b 单元被失活。
第3步，因为有 1−keep_prob 1 − k e e p _ p r o b 的单元失活了，这样 a3 a 3 的期望值也就减少了 1−keep_prob 1 − k e e p _ p r o b ， 所以我们要用 a3/keep_prob a 3 / k e e p _ p r o b ，这样 a3 a 3 的期望值不变。这就是inverted dropout。

这就是inverted dropout的内容。下面用两个动态图来演示下dropout的过程（素材来自ng的deep learning课）：

接下来主要来代码实现，假设我们的网络激活函数使用relu，输出层使用sigmoid，我们只要在前面一步步手写神经网络的基础上把前向传播（forward propagation）和后向传播（backward propagation）稍作修改就可以了：

前向传播（forward propagation）

def forward_propagation_with_dropout(X, parameters, keep_prob = 0.8):
    """
    X -- input dataset, of shape (input size, number of examples)
    parameters -- python dictionary containing your parameters "W1", "b1", "W2", "b2",...,"WL", "bL"
                    W -- weight matrix of shape (size of current layer, size of previous layer)
                    b -- bias vector of shape (size of current layer,1)
    keep_prob: probability of keeping a neuron active during drop-out, scalar
    :return:
    AL: the output of the last Layer(y_predict)
    caches: list, every element is a tuple:(W,b,z,A_pre)
    """
    np.random.seed(1)  #random seed
    L = len(parameters) // 2  #number of layer
    A = X
    caches = [(None,None,None,X,None)]  #用于存储每一层的，w,b,z,A,D第0层w,b,z用none代替
    # calculate from 1 to L-1 layer
    for l in range(1, L):
        A_pre = A
        W = parameters["W" + str(l)]
        b = parameters["b" + str(l)]
        z = np.dot(W, A_pre) + b  # 计算z = wx + b
        A = relu(z)  # relu activation function
        D = np.random.rand(A.shape[0], A.shape[1]) #initialize matrix D
        D = (D < keep_prob) #convert entries of D to 0 or 1 (using keep_prob as the threshold)
        A = np.multiply(A, D) #shut down some neurons of A
        A = A / keep_prob #scale the value of neurons that haven't been shut down
        caches.append((W, b, z, A,D))
    # calculate Lth layer
    WL = parameters["W" + str(L)]
    bL = parameters["b" + str(L)]
    zL = np.dot(WL, A) + bL
    AL = sigmoid(zL)
    caches.append((WL, bL, zL, A))
    return AL, caches

后向传播（backward propagation）

def backward_propagation_with_dropout(AL, Y, caches, keep_prob = 0.8):
    """
        Implement the backward propagation presented in figure 2.
        Arguments:
        X -- input dataset, of shape (input size, number of examples)
        Y -- true "label" vector (containing 0 if cat, 1 if non-cat)
        caches -- caches output from forward_propagation(),(W,b,z,pre_A)
        keep_prob: probability of keeping a neuron active during drop-out, scalar
        Returns:
        gradients -- A dictionary with the gradients with respect to dW,db
        """
    m = Y.shape[1]
    L = len(caches) - 1
    # print("L:   " + str(L))
    # calculate the Lth layer gradients
    prev_AL = caches[L - 1][3]
    dzL = 1. / m * (AL - Y)
    dWL = np.dot(dzL, prev_AL.T)
    dbL = np.sum(dzL, axis=1, keepdims=True)
    gradients = {"dW" + str(L): dWL, "db" + str(L): dbL}
    # calculate from L-1 to 1 layer gradients
    for l in reversed(range(1, L)): # L-1,L-2,...,1
        post_W = caches[l + 1][0]  # 要用后一层的W
        dz = dzL  # 用后一层的dz
        dal = np.dot(post_W.T, dz)
        Dl = caches[l][4] #当前层的D
        dal = np.multiply(dal, Dl) #Apply mask Dl to shut down the same neurons as during the forward propagation
        dal = dal / keep_prob #Scale the value of neurons that haven't been shut down
        Al = caches[l][3]  #当前层的A
        dzl = np.multiply(dal, relu_backward(Al))#也可以用dzl=np.multiply(dal, np.int64(Al > 0))来实现
        prev_A = caches[l-1][3]  # 前一层的A
        dWl = np.dot(dzl, prev_A.T)
        dbl = np.sum(dzl, axis=1, keepdims=True)

        gradients["dW" + str(l)] = dWl
        gradients["db" + str(l)] = dbl
        dzL = dzl  # 更新dz
    return gradients

关于dropout有几点是要非常注意的：

• 只有在训练网络的时候使用dropout，在测试集上（预测的时候）不要使用dropout，也就意味着我们在预测（分类）的时候，用训练好的参数做前向传播的时候，要把dropout关掉！
• dropout是一个正则化技术

下面我们在sklean中的load_breast_cancer数据集中来简单的对比下，无正则项的网络，带L2正则项的网络和带dropout的网络效果：

不带任何正则项的网络，准确率为：0.912

L2正则项的网络，准确率为：0.921

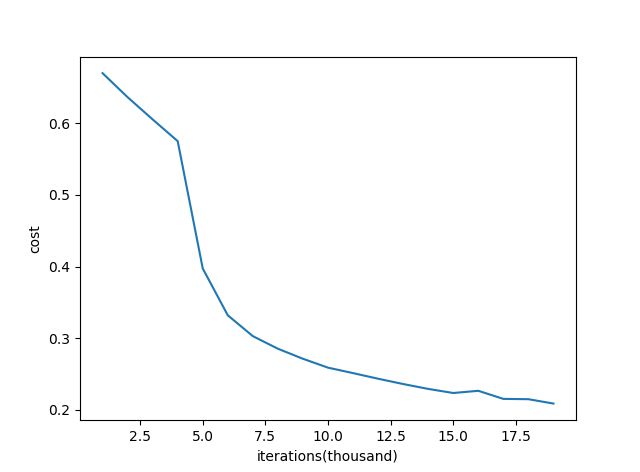
dropout正则项的网络，准确率为：0.929

完整的代码已经放到github上了：
带L2正则项的网络：deep_neural_network_with_L2
带dropout正则项的网络：deep_neural_network_with_dropout